在设计Machine Learning系统时,我们很难从系统运行之前就得知系统的“复杂程度”。在线性回归中,我们可以将此问题等同为:使用几维参数,是否需要涉及更复杂的多项式,以及本文的一个新概念—Regularization Parameter。本文,将讨论Underfit,Overfit基本理论,及如何改进系统复杂度,使其能够使其在准确拟合现有训练样例的情况下,尽可能准确预测新数据。
Underfit(欠拟合)和Overfit(过拟合)
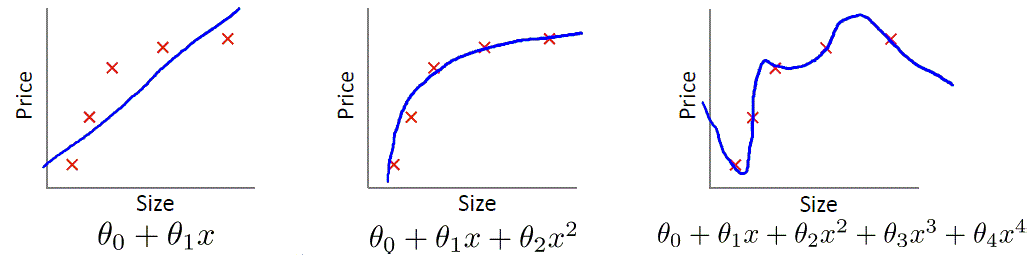
首先要确定的两个概念是Underfit(欠拟合)和Overfit(过拟合),也被称作high bias和high viarance。在表征线性回归模型的下面的三张图中,左图使用一条直线来作为模型,很明显无论如何调整起始点和斜率,该直线都不可能很好的拟合给定的五个训练样例,更不要说给出的新数据;右图使用了高阶的多项式,过于完美的拟合了训练样例,当给出新数据时,很可能会产生较大误差;而中间的模型则刚刚好,既较完美的拟合训练样例,又不过于复杂,基本上描绘清晰了在预测房屋价格时Size和Prize的关系。
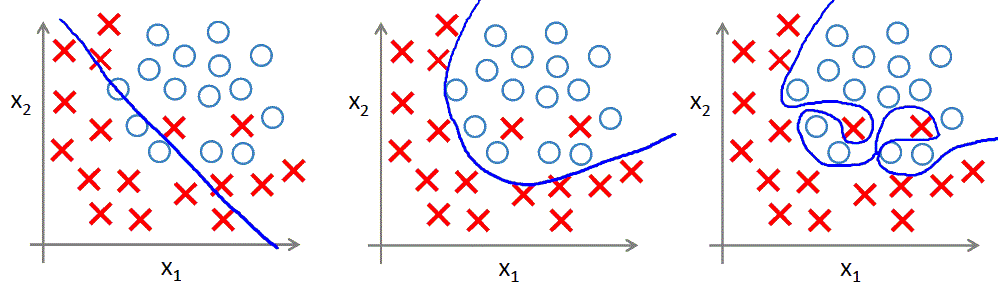
对于逻辑回归,同样存在此问题,如下图:
解决欠拟合或过拟合的思路
1、增减模型的参数维度。如利用线性回归预测房屋价格的例子中,增加“卧室数量”,“停车位数量”,“花园面积”等维度以解决欠拟合,或相应的减少维度去解决过拟合。
2、增减多项式维度,比如将加入高阶多项式来更好地拟合曲线,用以解决欠拟合,或者降阶去处理过拟合。
3、调整Regularization Parameter。在不改变模型参数维度和多项式维度的情况下,单纯的调整Regularization Parameter同样可以有效改变模型对数据的拟合程度。
Regularization Parameter
在之前做逻辑回归的Octave仿真时,就用到了该参数,我们可以看到在计算Cost Function时,加入了一项theta'*theta*lambda/(2*m),此项即为调整项。整理后的逻辑回归Cost Function和梯度下降求theta的表达式为如下形式:
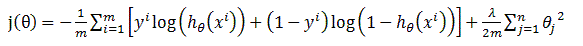
线性回归的Cost Function也是类似形式:
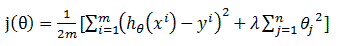

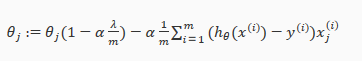
无论是哪一种模型,lambda的取值对于能否改进模型的表现都有很重要的作用。试想如果lambda取值过大,那么cost function的取值就近似于Regularization Parameter的取值,即为一条直线了,这同样是一种Underfit,而如果lambda取值过小,则对于cost function而言没有任何作用。在下篇文章中,会详细讲解如何评估模型表现及选取lambda的值。