
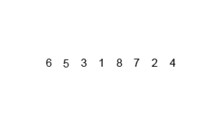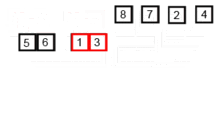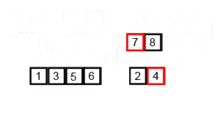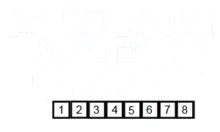
归并排序是创建在归并操作上的一种有效的排序算法,效率为O(nlogn)大O符号。1945年由约翰·冯·诺伊曼首次提出。该算法是采用分治法(Divide and Conquer)的一个非常典型的应用,且各层分治递归可以同时进行。
采用分治法:
- 分割:递归地把当前序列平均分割成两半。
- 集成:在保持元素顺序的同时将上一步得到的子序列集成到一起(归并)。
归并操作(merge),也叫归并算法,指的是将两个已经排序的序列合并成一个序列的操作。归并排序算法依赖归并操作。
递归法(Top-down)
- 申请空间,使其大小为两个已经排序序列之和,该空间用来存放合并后的序列
- 设定两个指针,最初位置分别为两个已经排序序列的起始位置
- 比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置
- 重复步骤3直到某一指针到达序列尾
- 将另一序列剩下的所有元素直接复制到合并序列尾
迭代法(Bottom-up)
原理如下(假设序列共有n个元素):
- 将序列每相邻两个数字进行归并操作,形成ceil(n/2)个序列,排序后每个序列包含两/一个元素
- 若此时序列数不是1个则将上述序列再次归并,形成ceil(n/4)个序列,每个序列包含四/三个元素
- 重复步骤2,直到所有元素排序完毕,即序列数为1
def mergeSort(nums):
if len(nums) < 2:
return nums
mid = len(nums) // 2
left = mergeSort(nums[:mid])
right = mergeSort(nums[mid:])
result = []
while left and right:
if left[0] <= right[0]:
result.append(left.pop(0))
else:
result.append(right.pop(0))
if left:
result += left
if right:
result += right
return result
if __name__ == "__main__":
nums = [1, 4, 2, 3.6, -1, 0, 25, -34, 8, 9, 1, 0]
print("original:", nums)
print("Sorted:", mergeSort(nums))
>>>
original: [1, 4, 2, 3.6, -1, 0, 25, -34, 8, 9, 1, 0]
Sorted: [-34, -1, 0, 0, 1, 1, 2, 3.6, 4, 8, 9, 25]
参考:https://zh.wikipedia.org/wiki/Wikipedia:%E9%A6%96%E9%A1%B5