首先 开始我读论文时 也是恨不得吃透每个单词 但是后来转念一想 没必要每个单词都弄懂
因为 一些程度副词 修饰性的形容词等 这些只能增强语气罢了 对文章主题的理解并没有天大的帮助
而读文章应该首先把握主旨 我们应该首要关注 标题 关键词 去通读一遍把握主旨 然后精读重要部分 接着提炼收获
读论文的步骤大致如下: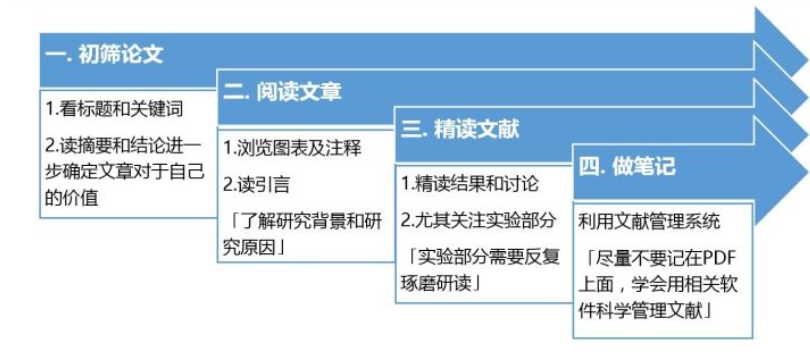
下面记录一下我开始如何读的英语论文
这篇论文是香港中文大学最近的论文

首先看标题 第二行肯定比较关键 通过了解查阅饲料 可以得到隐私保护集合求交技术(PSI)
而后边的摘要就是介绍了这种技术 简要概括一下
隐私保护集合交集协议允许持有各自集合的两方来共同计算两个集合的交集运算。在协议交互的最后,一方或是两方应该得到正确的交集,而且不会得到交集以外另一方集合中的任何信息。
而其中一些细节 关于t这个参数什么的 我真不明所以 resp我也不知道是什么的简写 response?那么保留这些问题
这么爱装杯的知乎都没人回答的么 不是我问的 老问题了

但是通过这句话可以初步知道 大约满足psi大于或者小于参数t 这类条件时 客户方应该才会获取信息
之后的这部分:
一些基础的介绍 个人认为没有实际价值
之后介绍的是赵和周的研究工作:

看到这里我还是一头雾水t是什么
可是后来
大致可以知道 这个c和s交互 c需要满足s的一些条件(s也可能要同时满足c的条件 因为交互一般都是双向的) 才能进行交互(获取交集的信息) 这个条件目前姑且认为是单调的 (t>psi的阈值或者t小于psi的阈值)
因为后边举了个例子 比如一个data(约会)软件 c与s交互 s肯定不想告诉c所有的东西 原因多方面:比如一是怕泄露太多用户隐私 二是怕c这一方会做出一些出格举动(毕竟男人都是lsp了)三是如果高强度交互数据 对服务器等成本也是种考验 这些考虑是出于谋求共同利益 “From the perspective of finding common interests”
那么这两个情况 或者说两种函数 我们姑且统称为 t>psi的阈值或者t小于psi的阈值 那么resp应该是“或”(or)
比如 这个软件 女用户也有需求 他们需要t>psi 来保证搜索到的男性的质量 比如 要帅 要有钱 要离得近 这种 此时的搜索就是求交集 而且是有条件地求交
当然女用户也有另一种需求 要t<psi 来过滤掉另一部分男性 (丑的 吸烟的 没钱的) 使得这部分人的出现次数低于可以接受的阈值
我认为我这些解释够形象了 隐私保护差不多就是这样
下一部分:

这一部分的概述说的是 我们讨论的那种单调问题还是最基本的 而光 t大于小于 这个问题 概念相似 实际上又是不同的问题
而世界上肯定也会存在非单调非线性的问题 这样问题本身更加复杂

之后提出 他们想要统一两种协议的设计 要用一种创新方法来实现这两种psi协议(也就是设计一种巧妙算法) 而不会去泄露交集的大小等相关信息
而赵和周面临了两个问题 一方面,应该有一种方法来快速识别哪些共享可以用来重建解锁密钥 另一方面,它通过对可能有用的单个共享的计数来揭示匹配的数量,即交集的大小
之后又引出了:存在PSI(简称PSI- x) existential PSI
PSI-X只输出一个位而不是一个位集。输出表示这两个私有集是否有任何重叠
特别地,我们又构建一个协议
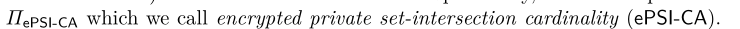
在这种设计中,基数不再是无意的泄漏,而是有意加密的。这为实现阈值功能提供了一个有用的基础
在这两种设计的基础上,都有一种对加密数据进行计算的技术,该技术通过无关多项式求值(OPE)实现。附录C总结了PSI变量之间的关系。 也就可以查阅了
之后
merits 总结的一些优点 这些可以不看了 无非就是复杂度小啊 什么的

这里说的呢 就是 这个协议本身也是有缺点的
尽管我们的协议是有效的,但它们仍然依赖于公钥技术,这种技术很难避免,而且不如对称密钥(比如哈希函数或块密码)高效
同时 PSI协议也常常是高度交互的 那么协议的进行肯定繁重而复杂
这里就想将其外包给云服务 将PSI外包出去,不仅效率更高,而且更符合移动应用的商业模式和使用习惯

1.4介绍了相关人员的研究工作
看完这些 大致对文章有了个初步了解 之后的才是重点和主体

这个preliminary有点烦人啊 主要是知识储备不够 后边那些算法什么的跟鬼一样 还都是英文的
上边的图  表示从集合S中取元素
表示从集合S中取元素
我们使用Fρ表示理想实现协议ρ的功能, 并使用Πρ表示ρ的具体的一些协议建设
而对于分布的X和Y不好区分 我们用一个negl函数表示

这个式子不太懂啊 保留问题

这个介绍的是同态加密和多项式求值
给定两个暗文Enc (pk, m0)和Enc (pk, m1),他们可以有效地计算加法Enc (pk, m0 + m1) = Enc (pk, m0)⊕Enc (pk, m1)不使用私钥sk
常数c,给定一个密文Enc (pk, m),一个可以很容易地计算Enc (pk, c·m)= c⊙Enc (pk, m)。
为了建立一个OPE协议,多项式p(x)可以通过加密其系数a0 ....来隐藏
这些加密系数,用Enc(pk, p(·))表示 任何持有明文s的人都可以使用加法和恒乘法计算加密p(s)为Enc(pk, a0)⊕(Enc(pk, a1)⊙s)⊕··⊕(Enc(pk, ak)⊙sk)

Bloom Filters m位的紧凑数组,它表示一个包含n个元素的集合S
它由一组k独立的哈希函数H = (h1,…hi)统一地将元素映射到[m]中的索引。
之后的那些我就略了
直接看主体
这个大致上的意思就是 p2(服务器)输出永远是⊥ ⊥这个符号我认为没必要纠结 反正不是正常输出 ⊥(垂直符号)本应该是正交的一种概念 我认为是逻辑学上的一种概念 也可能就是作者随手用的
作者也没有说明什么的

P1(通常被称为“客户端”),如果它的输出不是⊥,它对这个阈值策略是满意的 它不能区分是否由于C∩S =ϕ 或者是C和S不符合policy
完全可以从下方的数学公式表达看出

p2永远输出⊥ p1输出c和s的交集 不输出其他(满足条件时)
为了同时实现Ft≤-PSI和Ft≥-PSI 他们使用了encrypted PSI cardinality (ePSI-CA)
设S和C是一个预定定义域的子集。让(pk1,sk1)是同态加密方案的公开/秘密密钥对:

这个我觉得要重点看一下:

我们描述.....混合模型,而具体实例化FePSI-CAis延迟到第四节
接下来,我们以t≤-PSI为例来展示如何使用FePSI-CA作为构建块来轻松实现。我们对ePSI-CA和健忘多项式求值(OPE)的新组合的关键在于,我们使用OPE将Enc(pk1,|C∩S|)(即FePSI-CA的输出)转换为会话密钥K的加密,当且仅当|C∩S|∈[0,t]。如果|C∩S| /∈[0,t],评价结果是随机的,不包含关于K的信息。
p2i将从feps - ca获得的加密基数重新随机化为Enc(pk1,|C∩S| + r),使得p1在解密Enc(pk1, |c∩S| + r)之后对|C∩S| + r一无所知,但却可以明确地求值一个在|c∩S| + r的多项式。更具体地说,P2first准备了一个多项式p(·),其根为r, r + 1,…, r + t,并选择随机对称密钥K. P2 then在自己的公钥pk2下发送多项式p '(·)= r '·p(·)+K的加密系数。
这样,当p1通过加性同态评估(求值)|C∩S| + r的p '(·)时(见第2.1节),结果将是当且仅当|C∩S|≤t时K的加密;否则,它将加密一个随机数,而这个随机数不会显示K的任何信息(因为r '·p(·)是一次加密K,而P2only使用r ' 一次
从之前的明文(生成Enc(pk2, p’(|C∩S|+r))中去检索在|C∩S|+r处的p '(·)值 (哪个是正确的会话密钥K或者是一个随机值)p1将该密文(在图1的步骤(4)中表示为Enc(pk2, K '))随机化,用随机数r "进一步使其盲化,并要求p2解密。当且仅当|C∩S|≤t时,p1最终获得的是一个等于K的值K’。这个K’作为一个标记,显示交集|C∩S|是否低于阈值
The final step is to have P1and P2engage in
a normal ΠPSI, in which P1and P2uses CK′= {ci||K′} and SK= {si||K} as
input respectively. Hence P1can recover the intersection if it possesses the same
key K′= K.