机器学习：基于CART算法的决策树——分类树与回归树

一、分类树构建（实际上是一棵递归构建的二叉树，相关的理论就不介绍了）

import numpy as np

class CartClassificationTree:
    class Node:
        '''树节点类'''

        def __init__(self):
            self.value = None

            # 内部叶节点属性
            self.feature_index = None
            self.feature_value = None
            self.left = None
            self.right = None

        def __str__(self):
            if self.left:
                s = '内部节点<%s>:
' % self.feature_index
                ss = '[ >%s]-> %s' % (self.feature_value, self.left)
                s += '	' + ss.replace('
', '
	') + '
'
                ss = '[<=%s]-> %s' % (self.feature_value, self.right)
                s += '	' + ss.replace('
', '
	')
            else:
                s = '叶节点(%s)' % self.value
            return s

    def __init__(self, gini_threshold=0.01, gini_dec_threshold=0., min_samples_split=2):
        '''构造器函数'''
        # 基尼系数的阈值
        self.gini_threshold = gini_threshold
        # 基尼系数降低的阈值
        self.gini_dec_threshold = gini_dec_threshold
        # 数据集还可继续分割的最小样本数量
        self.min_samples_split = min_samples_split

    def _gini(self, y):
        '''计算基尼指数'''
        values = np.unique(y)

        s = 0.
        for v in values:
            y_sub = y[y == v]
            s += (y_sub.size / y.size) ** 2

        return 1 - s

    def _gini_split(self, y, feature, value):
        '''计算根据特征切分后的基尼指数'''
        # 根据特征的值将数据集拆分成两个子集
        indices = feature > value
        y1 = y[indices]
        y2 = y[~indices]

        # 分别计算两个子集的基尼系数
        gini1 = self._gini(y1)
        gini2 = self._gini(y2)

        # 计算分割后的基尼系数
        # gini(y, feature) = (|y1| * gini(y1) + |y2| * gini(y2)) / |y|
        gini = (y1.size * gini1 + y2.size * gini2) / y.size

        return gini

    def _get_split_points(self, feature):
        '''获得一个连续值特征的所有分割点'''
        # 获得一个特征所有出现过的值, 并排序.
        values = np.unique(feature)
        # 分割点为values中相邻两个点的中点.
        split_points = [(v1 + v2) / 2 for v1, v2 in zip(values[:-1], values[1:])]

        return split_points

    def _select_feature(self, X, y):
        '''选择划分特征'''
        # 最佳分割特征的index
        best_feature_index = None
        # 最佳分割点
        best_split_value = None

        min_gini = np.inf
        _, n = X.shape
        for feature_index in range(n):
            # 迭代每一个特征
            feature = X[:, feature_index]
            # 获得一个特征的所有分割点
            split_points = self._get_split_points(feature)
            for value in split_points:
                # 迭代每一个分割点value, 计算使用value分割后的数据集基尼系数.
                gini = self._gini_split(y, feature, value)
                # 找到更小的gini, 则更新分割特征和.
                if gini < min_gini:
                    min_gini = gini 
                    best_feature_index = feature_index
                    best_split_value = value

        # 判断分割后基尼系数的降低是否超过阈值
        if self._gini(y) - min_gini < self.gini_dec_threshold:
            best_feature_index = None
            best_split_value = None

        return best_feature_index, best_split_value, min_gini

    def _node_value(self, y):
        '''计算节点的值'''
        # 统计数据集中样本类标记的个数
        labels_count = np.bincount(y)
        # 节点值等于数据集中样本最多的类标记.
        return np.argmax(np.bincount(y))

    def _create_tree(self, X, y):
        '''生成树递归算法'''
        # 创建节点
        node = self.Node()
        # 计算节点的值, 等于y的均值.
        node.value = self._node_value(y)

        # 若当前数据集样本数量小于最小分割数量min_samples_split, 则返回叶节点.
        if y.size < self.min_samples_split:
            return node

        # 若当前数据集的基尼系数小于阈值gini_threshold, 则返回叶节点.
        if self._gini(y) < self.gini_threshold:
            return node

        # 选择最佳分割特征
        feature_index, feature_value, min_gini = self._select_feature(X, y)
        if feature_index is not None:
            # 如果存在适合分割特征, 当前节点为内部节点.
            node.feature_index = feature_index
            node.feature_value = feature_value

            # 根据已选特征及分割点将数据集划分成两个子集.
            feature = X[:, feature_index]
            indices = feature > feature_value
            X1, y1 = X[indices], y[indices]
            X2, y2 = X[~indices], y[~indices]

            # 使用数据子集创建左右子树.
            node.left = self._create_tree(X1, y1)
            node.right = self._create_tree(X2, y2)

        return node

    def _predict_one(self, x_test):
        '''对单个样本进行预测'''
        # 爬树一直爬到某叶节点为止, 返回叶节点的值.
        node = self.tree_
        while node.left:
            if x_test[node.feature_index] > node.feature_value:
                node = node.left
            else:
                node = node.right

        return node.value

    def train(self, X_train, y_train):
        '''训练决策树'''
        self.tree_ = self._create_tree(X_train, y_train)

    def predict(self, X_test):
        '''对测试集进行预测'''
        # 对每一个测试样本, 调用_predict_one, 将收集到的结果数组返回.
        return np.apply_along_axis(self._predict_one, axis=1, arr=X_test)

二、分类树项目实战

2.1 数据集获取（经典的鸢尾花数据集）

http://archive.ics.uci.edu/ml/machine-learning-databases/iris/

描述：

Attribute Information:
1. sepal length in cm
2. sepal width in cm
3. petal length in cm
4. petal width in cm
5. class:
-- Iris Setosa
-- Iris Versicolour
-- Iris Virginica

2.2 加载数据

import numpy as np
X=np.genfromtxt('F:/python_test/data/iris.data',delimiter=',',usecols=range(4),dtype=float)
print(X)
y=np.genfromtxt('F:/python_test/data/iris.data',delimiter=',',usecols=4,dtype=str)
print(y)

 2.3 分类标签的变换

from sklearn.preprocessing import LabelEncoder
le=LabelEncoder()
y=le.fit_transform(y)
print('变换之后的y：
',y)

2.4 训练模型以及计算精确度，分类的精确度达到了0.9777777777777777

 

cct = CartClassificationTree()
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.3)
cct.train(X_train,y_train)
from sklearn.metrics import accuracy_score
y_pred=cct.predict(X_test)
score=accuracy_score(y_test,y_pred)
print(score)

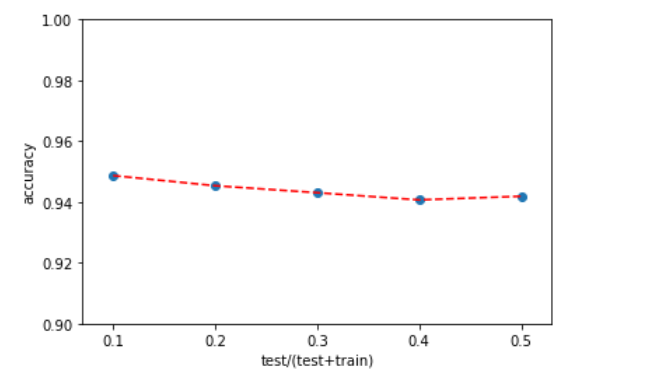
2.5 调整测试集大小，发现不管测试集划分为多大，最终的准确度大约都是94%

import matplotlib
matplotlib.use('TkAgg')
import matplotlib.pyplot as plt
plt.scatter(TEST_SIZE,SCORE)
plt.plot(TEST_SIZE,SCORE,'--',color='red')
plt.ylim([0.90,1.0])
plt.xlabel('test/(test+train)')
plt.ylabel('accuracy')
plt.show()

 三、回归树项目实战

3.1 回归树的代码（通过递归构建的二叉树，cart算法）

import numpy as np

class CartRegressionTree:
    class Node:
        '''树节点类'''

        def __init__(self):
            self.value = None

            # 内部叶节点属性
            self.feature_index = None
            self.feature_value = None
            self.left = None
            self.right = None

        def __str__(self):
            if self.left:
                s = '内部节点<%s>:
' % self.feature_index
                ss = '[ >%s]-> %s' % (self.feature_value, self.left)
                s += '	' + ss.replace('
', '
	') + '
'
                ss = '[<=%s]-> %s' % (self.feature_value, self.right)
                s += '	' + ss.replace('
', '
	')
            else:
                s = '叶节点(%s)' % self.value
            return s

    def __init__(self, mse_threshold=0.01, mse_dec_threshold=0., min_samples_split=2):
        '''构造器函数'''
        # mse的阈值
        self.mse_threshold = mse_threshold
        # mse降低的阈值
        self.mse_dec_threshold = mse_dec_threshold
        # 数据集还可继续分割的最小样本数量
        self.min_samples_split = min_samples_split

    def _mse(self, y):
        '''计算MSE'''
        # 估计值为y的均值, 因此均方误差即方差.
        return np.var(y)

    def _mse_split(self, y, feature, value):
        '''计算根据特征切分后的MSE'''
        # 根据特征的值将数据集拆分成两个子集
        indices = feature > value
        y1 = y[indices]
        y2 = y[~indices]

        # 分别计算两个子集的均方误差
        mse1 = self._mse(y1)
        mse2 = self._mse(y2)

        # 计算划分后的总均方误差
        return (y1.size * mse1 + y2.size * mse2) / y.size

    def _get_split_points(self, feature):
        '''获得一个连续值特征的所有分割点'''
        # 获得一个特征所有出现过的值, 并排序.
        values = np.unique(feature)
        # 分割点为values中相邻两个点的中点.
        split_points = [(v1 + v2) / 2 for v1, v2 in zip(values[:-1], values[1:])]

        return split_points

    def _select_feature(self, X, y):
        '''选择划分特征'''
        # 最佳分割特征的index
        best_feature_index = None
        # 最佳分割点
        best_split_value = None

        min_mse = np.inf
        _, n = X.shape
        for feature_index in range(n):
            # 迭代每一个特征
            feature = X[:, feature_index]
            # 获得一个特征的所有分割点
            split_points = self._get_split_points(feature)
            for value in split_points:
                # 迭代每一个分割点value, 计算使用value分割后的数据集mse.
                mse = self._mse_split(y, feature, value)
                # 找到更小的mse, 则更新分割特征和.
                if mse < min_mse:
                    min_mse = mse 
                    best_feature_index = feature_index
                    best_split_value = value

        # 判断分割后mse的降低是否超过阈值, 如果没有超过, 则找不到适合分割特征.
        if self._mse(y) - min_mse < self.mse_dec_threshold:
            best_feature_index = None
            best_split_value = None

        return best_feature_index, best_split_value, min_mse

    def _node_value(self, y):
        '''计算节点的值'''
        # 节点值等于样本均值
        return np.mean(y)

    def _create_tree(self, X, y):
        '''生成树递归算法'''
        # 创建节点
        node = self.Node()
        # 计算节点的值, 等于y的均值.
        node.value = self._node_value(y)

        # 若当前数据集样本数量小于最小分割数量min_samples_split, 则返回叶节点.
        if y.size < self.min_samples_split:
            return node

        # 若当前数据集的mse小于阈值mse_threshold, 则返回叶节点.
        if self._mse(y) < self.mse_threshold:
            return node

        # 选择最佳分割特征
        feature_index, feature_value, min_mse = self._select_feature(X, y)
        if feature_index is not None:
            # 如果存在适合分割特征, 当前节点为内部节点.
            node.feature_index = feature_index
            node.feature_value = feature_value

            # 根据已选特征及分割点将数据集划分成两个子集.
            feature = X[:, feature_index]
            indices = feature > feature_value
            X1, y1 = X[indices], y[indices]
            X2, y2 = X[~indices], y[~indices]

            # 使用数据子集创建左右子树.
            node.left = self._create_tree(X1, y1)
            node.right = self._create_tree(X2, y2)

        return node

    def _predict_one(self, x_test):
        '''对单个样本进行预测'''
        # 爬树一直爬到某叶节点为止, 返回叶节点的值.
        node = self.tree_
        while node.left:
            if x_test[node.feature_index] > node.feature_value:
                node = node.left
            else:
                node = node.right

        return node.value

    def train(self, X_train, y_train):
        '''训练决策树'''
        self.tree_ = self._create_tree(X_train, y_train)

    def predict(self, X_test):
        '''对测试集进行预测'''
        # 对每一个测试样本, 调用_predict_one, 将收集到的结果数组返回.
        return np.apply_along_axis(self._predict_one, axis=1, arr=X_test)

3.2 数据集的获取

http://archive.ics.uci.edu/ml/machine-learning-databases/housing/

3.3 加载数据集

import numpy as np
dataset=np.genfromtxt('F:/python_test/data/housing.data',dtype=np.float)
print(dataset)

 3.4 数据集的划分、模型的训练与预测

X=dataset[:,:-1]
y=dataset[:,-1]
crt=CartRegressionTree()
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.3)
crt.train(X_train,y_train)
from sklearn.metrics import accuracy_score
y_predict = crt.predict(X_test)
crt.predict(X_test)

3.5 量化模型预测的误差，实际上使用mae比较好，可以看出价格预测的偏差大小大约是3036美元

from sklearn.metrics import mean_squared_error,mean_absolute_error
mse=mean_squared_error(y_test,y_predict)
mae=mean_absolute_error(y_test,y_predict)
print('均方差：',mse)
print('平均绝对误差：',mae)

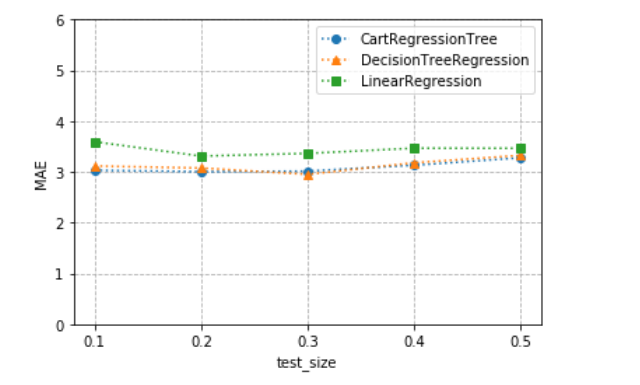
 3.6 调用sklearn中的线性回归与决策树回归模型与我们的CartDecisionTree进行比较，将计算分为5组（5中test_size），每组都进行十次，得到三个mae和mse的值，绘制在图像中

我们可以发现我们的决策树回归算法和sklearn中的决策树回归算法准确度一致，都比LinearRegression效果要好,经过对mse的测试我们发现我们编写的算法比两种算法都优秀一些，线性回归算法

在三种算法中质量是最差的。

import numpy as np
from sklearn.tree import DecisionTreeRegressor
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error,mean_absolute_error
from sklearn.model_selection import train_test_split
import matplotlib
matplotlib.use('TkAgg')
import matplotlib.pyplot as plt
import numpy as np
dataset=np.genfromtxt('F:/python_test/data/housing.data',dtype=np.float)
X=dataset[:,:-1]
y=dataset[:,-1]

#使用三维数组来存储mae
mae_array=np.empty((5,10,3))
mse_array=np.empty((5,10,3))
#产生五个test_size,步长是0.1,包括尾部
test_size=np.linspace(0.1,0.5,5)
for i,size in enumerate(test_size):
    for j in range(10):
        X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=size)
        
        crt = CartRegressionTree()
        crt.train(X_train,y_train)
        y_pred=crt.predict(X_test)
        mae_array[i,j,0] = mean_absolute_error(y_test,y_pred)
        mse_array[i,j,0] = mean_squared_error(y_test,y_pred)
        
        dtr = DecisionTreeRegressor()
        dtr.fit(X_train,y_train)
        y_pred=dtr.predict(X_test)
        mae_array[i,j,1] = mean_absolute_error(y_test,y_pred)
        mse_array[i,j,1] = mean_squared_error(y_test,y_pred)
        
        lr=LinearRegression()
        lr.fit(X_train,y_train)
        y_pred=lr.predict(X_test)
        mae_array[i,j,2] = mean_absolute_error(y_test,y_pred)
        mse_array[i,j,2] = mean_squared_error(y_test,y_pred)

#计算均值，5*3的矩阵,由于列才是axis=0的部分，所以要将矩阵转置输出
Y=mae_array.mean(axis=1).T
plt.plot(test_size,Y[0],'o:',label='CartRegressionTree')
plt.plot(test_size,Y[1],'^:',label='DecisionTreeRegression')
plt.plot(test_size,Y[2],'s:',label='LinearRegression')
plt.xlabel('test_size')
plt.ylabel('MAE')
plt.xticks(test_size)
plt.ylim([0.0,6.0])
plt.yticks(np.arange(0.0,6.1,1.0))
plt.grid(linestyle='--')
plt.legend()
plt.show()

Y=mse_array.mean(axis=1).T
plt.plot(test_size,Y[0],'o:',label='CartRegressionTree')
plt.plot(test_size,Y[1],'^:',label='DecisionTreeRegression')
plt.plot(test_size,Y[2],'s:',label='LinearRegression')
plt.xlabel('test_size')
plt.ylabel('MSE')
plt.xticks(test_size)
# plt.ylim([0.0,6.0])
# plt.yticks(np.arange(0.0,6.1,1.0))
plt.grid(linestyle='--')
plt.legend()
plt.show()