一.二叉排序树产生原因
二叉排序树又叫做二叉搜索树,为什么要有二叉排序树这种数据结构的产生?对于一个既要排序、又要支持高效的查找、插入和删除操作的数据元素集合,将其组织成一个什么样的数据结构能够满足要求?我们对于排序顺序表、排序单链表和散列表这几种数据结构进行分析:
(1)排序顺序表,可以采用折半查找法,时间效率为O(log2n);插入和删除的操作时间复杂度为O(n),数据移动量大,效率较低。
(2)排序单链表,顺序查找的时间效率为O(n),不能采用折半查找算法;插入和删除操作的时间复杂度为O(n),虽然没有数据移动但因为查询找效率低下,使得插入和删除的效率也较低。
(3)散列表,虽然查找、插入和删除操作的效率较高,但是散列表不具有排序特性。
上述几种数据结构不能满足问题的要求。我们一树结构来研究这个问题。
二叉排序树是一种既支持排序、又支持高效的查找、插入和删除操作的数据组织方案,她的查找等操作效率可达到O(log2n)。
在一棵二叉树中查找一个节点,需要在遍历二叉树的过程中对节点逐个进行比较,这是顺序查找算法,查找效率为O(n)。如果一颗二叉树是排序的,则没经过一次比较,根据比较结果,可在当前节点的左子树和右子树中选择其一继续,从而将查找范围缩小了一半, 一次查找只需要经过从根到某节点的一条路径就可获得查找结果,比较次数最多是二叉树的高度,查找效率为O(log2n)。远低于O(n).
二、二叉排序树的定义
二叉排序树或者是一棵空树,或者是具有下列性质的二叉树;
(1)每个结点都有一个作为查找一句的关键字,所有结点的关键字互不相同。
(2)若一个结点的左子树不空,则左子树上所有结点的关键字均小于这个结点的关键字;若一个结点的右子树不为空,则右子树上所有结点的关键字均大于这个结点的关键字。
(3)每个结点的左、右子树也分别为二叉排序树。
一个二叉排序树中序遍历得到的关键字是升序的。如图一所示,得到的关键字圣墟排列的数据元素序列为{6,12,18,36,54,57,66,76,81,87,99};
 图一
图一
三、二叉树的查找
在一棵二叉排序树中,查找关键字key元素结点,算法描述如下:
(1)从根节点开始,设p指向根节点
(2)将p结点的关键字与key比较,若两者相等,则查找成功;若key较小,则在p的左子树中继续查找;若key较大,则在p的右子树中继续查找。
(3)重复执行上一步,直到查找成功或p为空。若p为空,则查找不成功。
二叉排序树中,查找的过程如图二所示。在查找76的路径是{54,66,87,76},到达终点76,查找成功;查找40的路径是{54,18,36},经过叶子节点36查找不成功。由此可知,在二叉排序树中,
一次查找经过从根结点到某结点的一条路径而不需要遍历整个二叉排序树,若查找成功则到达指定节点,否则经过某个叶子节点。因此,二叉排序树能够提供快速的查找功能。二叉排序树又称为二叉查找树。
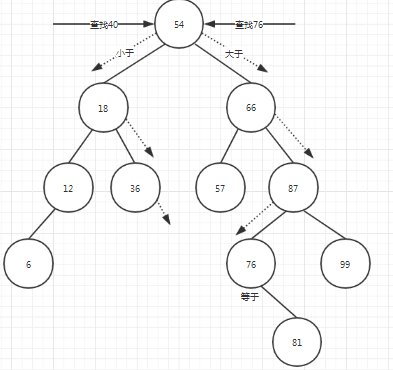
图二
四、二叉排序树的插入
一棵二叉排序树,插入一个结点之后必须仍然是二叉排序树。每插入一个结点,首先需要找到该结点在二叉排序树中的插入位置,若具有相同关键字的结点已经在二叉排序树中,则不插入;否则将新结点作为椰子结点连接在其查找不成功的一条路径之尾,
该路径从根结点到某个原叶子结点。因此,给定一棵二叉树,一个结点的插入位置是唯一的。例如在图二中,欲插入40,查找40的路径是(54,18,36),查找不成功,将结点40作为原叶子结点36的右孩子插入到该棵二叉排序树中。
五、二叉排序树的删除
在二拆排序树中删除一个结点,首先查找该节点,若存在,则根据结点的度对二叉排序树进行不同程度的调整,使删除结点后的二叉树仍然是二叉排序树。
设p指向待删除的结点,parent指向p的父结点。根据p的维度不同,二叉排序树的删除算法分以下三种算法。
(1)p是叶子结点。若p是parent的左孩子,删除p结点并设置parent的left链为空;若p是右孩子,删除p结点并设置parent的right链为空。
(2)p是1度结点,删除p结点并用p的孩子填补作为parent的孩子,共有四中情况。
a.若p是parent的左孩子且p有左孩子,设置parent的left链指向p的左孩子。
b.若p是parent的左孩子且p有右孩子,设置parent的left链指向p的右孩子。
c.若p是parent的右孩子且p有左孩子,设置parent的right链指向p的左孩子。
d.若p是parent的右孩子且p有右孩子,设置parent的right链指向p的右孩子。
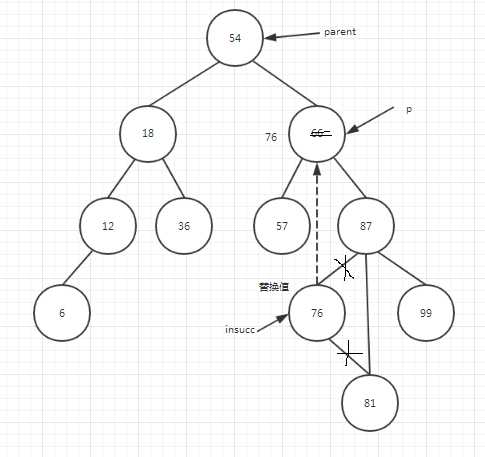
(3)p是2度结点,不直接删除p结点,而是先用p的中根次序下的后继空额到吗insucc值代替p结点值,再删除insucc结点。这样将删除2度结点问题转换为删除1度结点或叶子结点,使得对二叉排序树的调整减少到最小程度。删除二度结点p的操作如图三所示