(震惊, 009 莫得 F.)
(啊我发现自己错字 typo 好多 qwq.)
「AGC 007C」Pushing Balls
Tag:「C.性质/结论」
这个期望直观上太均匀了!
记当前期望局面为 \(\lang n,d,x\rang\), 通过模拟单次选球, 将剩下的球坑重编号, 可以发现后继期望局面为 \(\lang n-1,(2d+5x)/(2n),x+2x/n\rang\), 当前操作的期望距离为 \(d+(2n-1)/2\cdot x\). \(\mathcal O(n)\) 递推一下就做完了.
「AGC 007D」Shik and Game
Tag:「水题无 tag」
??? 你放一道伞兵得令人发指的 DP 题搁这儿做慈善呢还是当难度刺客呢 ???
\(f(i)\) 表示从 \(x_i\) 出发操作完后缀并走到出口的最小用时, \(f(n+1)=0\). 转移是
当 \(\max\) 取前面的时候, 贪心地想, 必然只有 \(j\) 取临界位置时可能最优 (如果可以再往后送一颗糖果再往回, 又不浪费时间, 何乐而不为). 当 \(\max\) 取后面的时候, 显然可以直接维护最优转移. 所以 \(\mathcal O(n)\) 结束了.
「AGC 007E」Shik and Travel ^
Tags:「A.DP-树上 DP」「C.性质/结论」
二分答案 \(L\), 暴力 DP: 令 \(f(u,a,b)\) 表示 \(u\) 子树内, 从到 \(u\) 距离为 \(a\) 的叶子出发, 到距离为 \(b\) 的叶子结束, 路径长度不超过 \(L\), 是否可以遍历完子树. 那么转移为:
注意到注意到若 \(f(u,a_1,b_1)\) 为真, 那么 \(f(u,a_2,b_2)~(a_1\le a_2,b_1\le b_2)\) 都没有用. 暴力存储剩下的所有状态, 可以证明状态数不超过 \(\mathcal O(n\log n)\) (当时绝对证过, 这里跳了), 转移可以 two-pointers. 于是最终复杂度 \(\mathcal O(n\log n\log V)\).
「AGC 007F」Shik and Copying String *
Tag:「C.性质/结论」
字符的配对方式是显然的: 找到前缀最近的可用字符配对. 关键是在于求出最少步数. 盗张图:
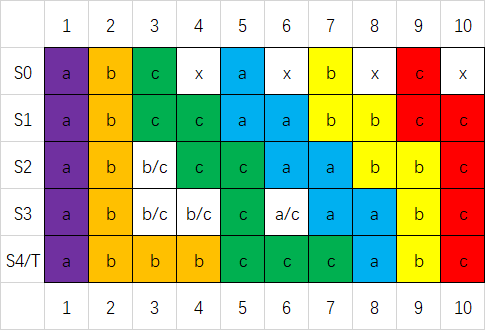
关注所有 L 形拐弯, 这些拐点的覆盖关系限定了一些字符向后覆盖的先后顺序. 我们从底层的 \(T\) 出发, 从后往前模拟这个过程. 沿着 \(y=x+b\) 的方向将拐点分类, 每类拐点只需要记录最上方的位置. 此后, 如果存在一个拐点无法左下延伸到当前考虑的 \(T_i\), 那么当前 \(T_i\) 的覆盖与这个拐点就没有以来关系, 可以将拐点删掉. 队列大小的最大值就是答案. 复杂度 \(\mathcal O(n)\).
「AGC 008C」Tetromino Tiling
Tag:「水题无 tag」
由于没有办法填平突出的一格, 第 \(3,6,7\) 种显然没用. 记剩下四种的数量分别为 \(a,b,c,d\), 除了一个特殊情况 \(4+1+5\) 的组合, 其他的组合形式都是同种内部组成 \(2\times 2k\). 注意特殊组合最多出现一次 (否则可以将两个一起拆开), 那么算出出现和不出现两种情况的答案求一个最大值即可.
那什么, 兔在这题的 attempt 次数是前 \(7\) 场到现在以来的最大值. (悲
「AGC 008D」K-th K
Tag:「水题无 tag」
从左往右贪心放需要放的, 然后从右往左贪心放快要不能放的. \(\mathcal O(n)\).
「AGC 008E」Next or Nextnext *
Tags:「A.DP-计数 DP」「B.模型转化」
怎么说呢, 太会容斥导致忽略了很多更为直接的思考途径.
设生成序列 \(a\) 的是某个排列 \(p\). 则 \(\{\lang i,p_i\rang\}\) 构成若干环. 现在允许将一些 \(\lang i,p_i\rang\) 替换为 \(\lang i,p_{p_i}\rang\) 来生成 \(\lang i,a_i\rang\). 每个 \(p\) 上的环显然是独立的, 我们分别讨论.
第一种情况, 环上所有边全部向后跳一步. 这时 \(a\) 的形状由 \(p\) 的环长奇偶性决定:
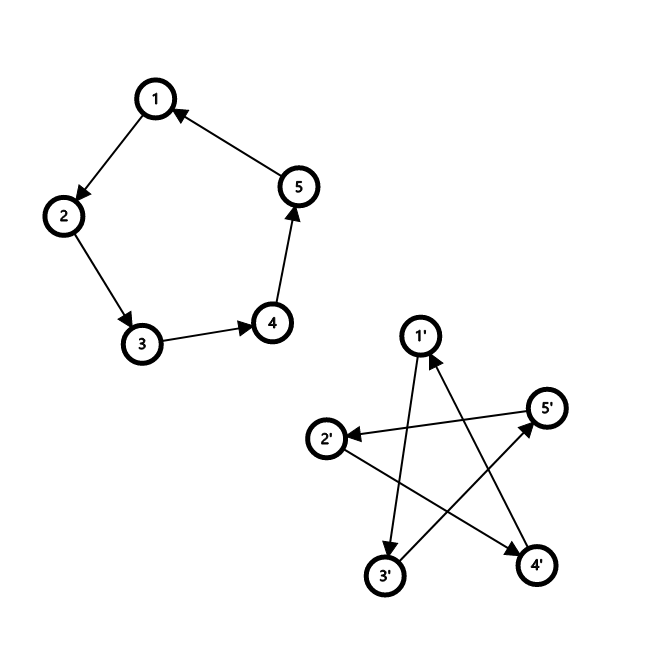
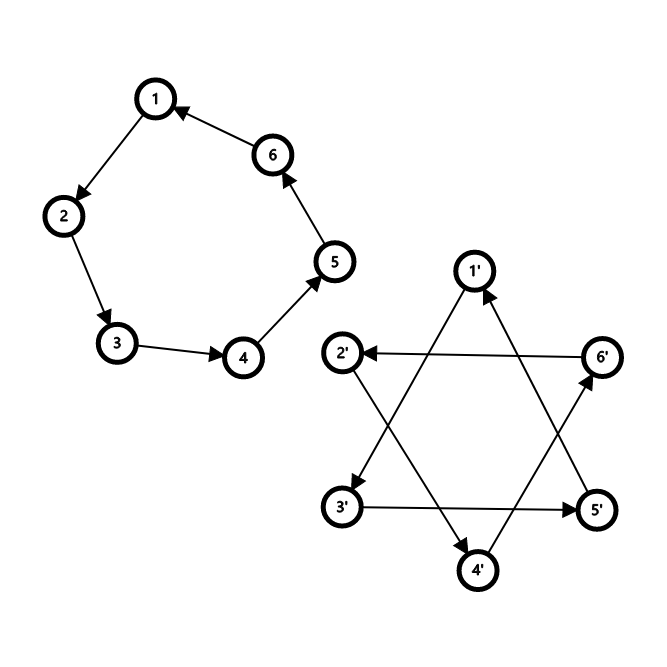
可见, 在奇环上, 这种变换不会改变环的结构; 偶环上则会把大环等分为两个小环.
第二种情况, 环上部分边向后跳, 部分边保留. 例如:
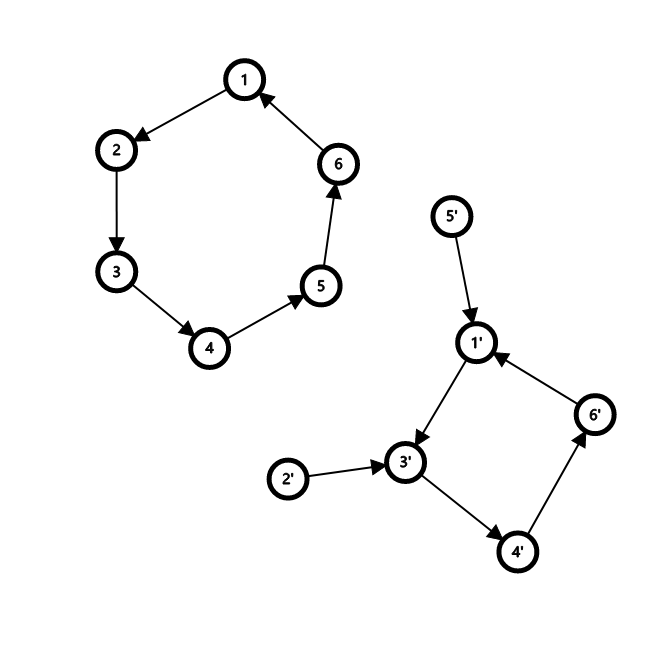
得到的 \(a\) 一定是内向基环树.
现在我们已知 \(a\), 反过来讨论 \(p\). 对于 \(a\) 中的简单环, 它必然由第一种情况生成. 大小相同的环可以合并出偶环, 所以将这些环按照大小分类, 每类做一个 DP 即可求出方案.
对于 \(a\) 中的基环树, 他必然有第二种情况生成. 我们需要做的是将环外挂的链给塞回环中.首先, 外挂链塞回后不能重叠 (上图中, \(2'\) 只能塞到 \(1'\rightarrow 3'\) 中, \(5'\) 只能塞到 \(3'\rightarrow 4'\rightarrow 6'\rightarrow 1'\) 中). 发现其实最多两种塞法: 全部跳这塞, 或者第一个不跳, 其他的跳这塞. 前者要求可塞范围 \(>\) 链长, 后者要求 \(\ge\) 链长. \(\mathcal O(n)\) 在环上扫一扫求能求出答案. 最终复杂度 \(\mathcal O(n)\).
「AGC 008F」Black Radius *
Tags:「C.性质/结论」「C.思维」
感觉这种需要磨结论的题总是磨到一般就放弃了 qwq.
先考虑部分分: 所有结点都可以是圆心的情况. 对于一个圆, 它可能是树上多个结点不同半径的临域. 设点集 \(D(u,r)\) 表示 \(u\) 的半径为 \(r\) 的树上临域, 我们的第一个任务就是找到不重不漏地计数圆的规则.
首先排除一个极其特殊的圆: \(V\) (完整点集). 设 \(R_u\) 表示 \(u\) 到其他点的最远距离, 则我们先对 \(u\) 限定 \(r<R_u\). 到此, 可以直观地感受到, 如果两个临域 \(D_1,D_2\) 对应了同一个圆, 则其中一个圆 "卡在了边界", 而另一个圆 "更靠中间", 与之对应的一个观察是, 若 \(D(u,r_1)=D(v,r_2)\neq V\), 则 \(r_1\neq r_2\), 证明是显然的.
因此, 对于圆 \(C\), 我们可以尝试在 \(D(u,r)=C\) 中使得 \(r\) 最小的临域 \(D(u_0,r_0)\) 处对 \(C\) 计数. 而检查 \(D(u_0,r_0)\) 可计数的条件便是: 不存在 \(u_0\) 的临接点 \(v\), 使得 \(D(u_0,r_0)=D(v,r_0-1)\). 以 \(u_0\) 为树根, 可以发现, 为了使 \(D(u_0,r_0)=D(v,r_0-1)\), \(v\) 应当取 \(u\) 最深邻接子树的树根. 那么相反的, 我们要求这个 \(v\) 仍不合法, 相当于要求 \(r_0\le t+1\), 其中 \(t\) 为 \(u_0\) 的次深邻接子树深度.
这就是部分分的情况. 现在推进到完整题目, 我们的计数规则需要变为: 在 \(D(u_0,r_0)\) 处, 若存在某个可作圆心的 \(v\), 使得 \(D(v,r)=D(u_0,r_0)\), 则计数 \(D(u_0,r_0)\) (注意并不要求 \(u_0\) 可作圆心). 类似于已有的讨论, 当圆心从 \(u\) 移动向 \(v\) 时存在 \(r\), 就势必满足 \(u_0\) 为根时, \(D(u_0,r_0)\) 覆盖了 \(v\) 这个方向的 \(u_0\) 的邻接子树的全部结点. 为了使这一条件宽松, \(v\) 就会在深度最浅的邻接子树里取 (当然, 前提是这棵子树里有圆心).
最后, 我们通过换根 DP 求出 \(D(u_0,r_0)\) 中 \(r_0\) 的上界和下界, 这一区间内的 \(r_0\) 都可被计数, 而后别忘记加上特殊的圆 \(V\). 这样就 \(\mathcal O(n)\) 做完啦.
「AGC 009C」Division into Two
Tag:「水题无 tag」
\(f_{A/B}(i,j)\) 表示考虑了前 \(i\) 个数, 第 \(i\) 个属于 \(A/B\), 属于另一个集合的最后一个是 \(j\). 滚个前缀和可以 \(\mathcal O(1)\) 整体转移 \(j\), 复杂度 \(\mathcal O(n)\).
「AGC 009D」Uninity *
Tags:「B.模型转化」「B.贪心」
一开始只想到点分树方面的东西, 然后就尝试开始讨论重心等等贪心方法, 结果忽略了转化求解目标的重要性 qwq.
对于这种递归式的划分, 一个常见的思路是将划分完成后的划分信息全部表现在原结构上. 在这里, 我们为 \(k-\)Uninity 划分的中心点编号上 \(k\), 可以发现, 编号合法的充要条件是: 任意两个标号为 \(k\) 的点的路径上存在一个标号为 \(k+1\) 的点.
当然啦, 点分树这个思路还是有点作用, 它提示我们, 需要使用的最大标号是 \(\log n\) 级别的.
所以 ... 就直接子树内状压 DP 贪心嘛. 完成子树的构造后, 得到一个集合 \(S\), 表示子树内能够经过不大于自己标号的点走到子树根以上的标号集合, 在合并孩子时考虑当前子树根的最小可能标号 \(x\). 则 \(x\) 应当满足:
- 对于所有孩子的 \(S\), \(x\notin S\);
- 若两个孩子的 \(S_1\cap S_2\neq\varnothing\), 则 \(x>\max(S_1\cap S_2)\).
灵活位运算维护这一过程可以做到 \(\mathcal O(n\log n/\omega)\), 当然这里也就是 \(\mathcal O(n)\).
「AGC 009E」Eternal Average ^
Tags:「A.DP-计数 DP」「B.模型转化」
显然先整棵 \(k\) 叉树, 设 \(1\) 叶子的深度集合为 \(\{p_m\}\), \(0\) 叶子的深度集合为 \(\{q_n\}\), 则根的值为 \(\sum_ik^{-p_i}\). 不过, 当务之急是找到根据 \(\{p_m\},\{q_n\}\) 反过来判定树是否存在的方法
唔 ... 有一个必要条件是 \(1=\sum_ik^{-p_i}+\sum_ik^{-q_i}\). 进一步思考发现, 我们的确可以通过这个必要条件构造出树: 将深度最大的结点凑在一起, 因为和为 \(1\), 所以必然存在 \(k\) 的倍数个, 将它们按任意顺序合并, 之后进行归纳构造即可.
现在, 问题转化成, 求有理数 \(x\) 的个数, 满足存在一组 \(\{p_m\},\{q_n\}\), 使得 \(x=\sum_ik^{-p_i}\) 且 \(1-x=\sum_ik^{-q_i}\). 尝试对 \(x=0.x_1x_2x_3\dots x_l\) 进行 DP. 考虑到原本的 \(\sum_ik^{-p_i}\) 可能有进位情况, 所以 \(\sum_ix_i\equiv m\pmod{k-1}\), 另一方面, \(y=1-x=0.y_1y_2y_3\dots y_l\), 自然有 \(\sum_iy_i=l(k-1)+1-\sum_ix_i\equiv n\pmod{k-1}\). 令 \(f(i,j)\) 表示考虑了 \(0.x_1x_2\dots x_i\), \(\sum_kx_k=j\) 时所有可能的 \(x\), 顺便限制小数点最后以为 \(\neq0\), \(\mathcal O((n+m)\min\{n,m\})\) 即可完成转移.