p1870长为m的字典序最大不下降子序列

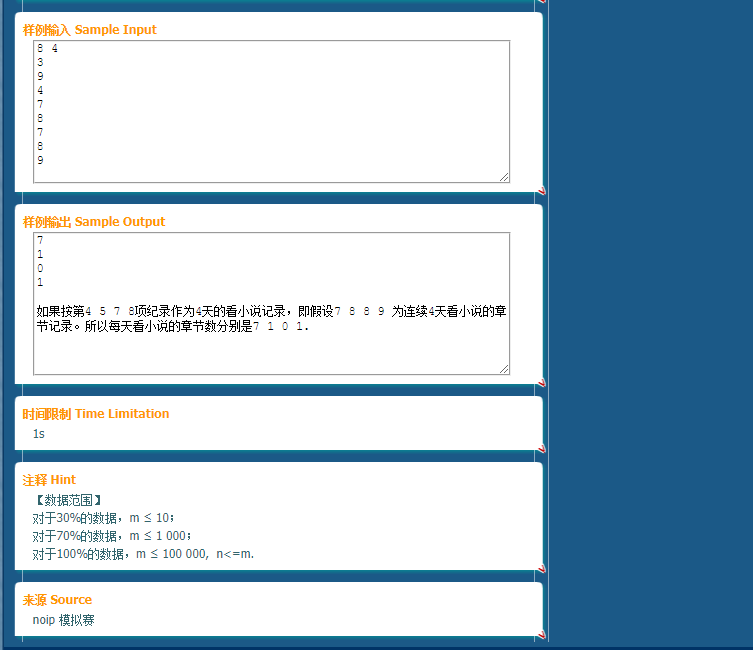
　　首先理解题意。一句话翻译就是：给出长为m的数列求长为n的字典序最大不下降子序列。

　　看到只有两个人过，看似很难，实际上。。确实很难，从夏天见到的这个题就开始想并得到了一个错误算法，想了好长时间。

        首先二分求lis应该都会吧。首先处理出以每个点为起点的最长不下降序列长度len，考虑对于第i个元素我们要找的是哪个呢？应该是当前 值大于等于第i-1个元素 且 位置位于第i-1个元素之后 且 len大于等于n-i的那个数字。如果有同样大的元素应该取最靠前的那个。

　　 这样两个贪心策略就有了。可以先写结构体把元素按len排序，然后写一个堆：每次把len符合要求的全部放进去，由于是有序的，这个操作很快。然后把不符合要求的扔掉，最后留下来的堆顶一定是需要的元素，更新一下状态输出即可。

　　

int i,j,k,now;
int a[100010],c[100010],len;
int n,m;
priority_queue<pair <int,int> > o;
struct node
{
    int num;
    int j,len;
}shu[140000];
inline bool Orz(node xx,node yy)
{
    if(xx.len==yy.len)
    {
        return xx.j>yy.j;
    }
    return xx.len>yy.len;
}
inline int ask(int x)
{
    int l=1,r=len,mid;
    while(l<=r)
    {
        mid=(l+r)>>1;
        if(x<=c[mid])l=mid+1;
        else
            r=mid-1;
    }
    return l;
}

int main()
{
    n=read();m=read();
    for(i=1;i<=n;i++)
    {
        a[i]=shu[i].num=read();
        shu[i].j=i;
    }
    for(i=n;i>=1;i--)
    {
        shu[i].len=k=ask(shu[i].num);
        c[k]=shu[i].num;
        len=max(len,k);
    }
    sort(shu+1,shu+1+n,Orz);
    for(k=0,i=1;m;m--)
    {
        while(shu[i].len>=m&&i<=n)
        {
            o.push(make_pair(shu[i].num,-shu[i].j));
            i++;
        }
        while(o.size()&&(o.top().first<now||-o.top().second<=k))
            o.pop();
        cout<<o.top().first-now<<endl;
        now=o.top().first;
        k=-o.top().second;
    }
}

　　最后分析一下复杂度：二分求lis复杂度(n*logn)，sort复杂度(n*logn)，最后的操作i移动的n次，每个元素最多进堆一次出堆一次，复杂度(n*logn);总体复杂度n*logn