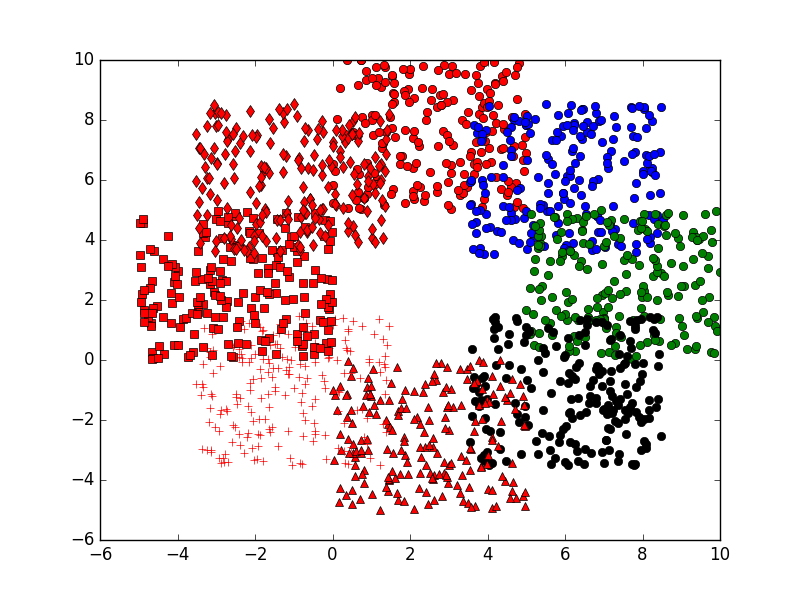
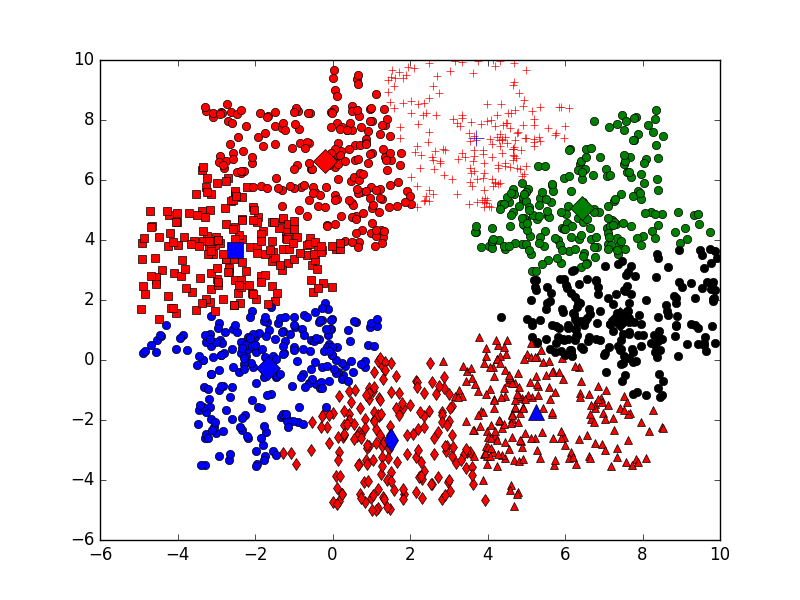
KMeans算法
基本思想是初始随机给定K个簇中心,按照最邻近原则把待分类样本点分到各个簇。然后按平均法重新计算各个簇的质心,从而确定新的簇心。一直迭代,直到簇心的移动距离小于某个给定的值。
k-means 算法接受输入量 k ;然后将n个数据对象划分为 k个聚类以便使得所获得的聚类满足:同一聚类中的对象相似度较高;而不同聚类中的对象相似度较小。聚类相似度是利用各聚类中对象的均值所获得一个“中心对象”(引力中心)来进行计算的。
k-means 算法基本步骤
(1) 从 n个数据对象任意选择 k 个对象作为初始聚类中心;
(2) 根据每个聚类对象的均值(中心对象),计算每个对象与这些中心对象的距离;并根据最小距离重新对相应对象进行划分;
(3) 重新计算每个(有变化)聚类的均值(中心对象);
(4) 计算标准测度函数,当满足一定条件,如函数收敛时,则算法终止;如果条件不满足则回到步骤(2)。
算法分析和评价
k-means 算法接受输入量 k ;然后将n个数据对象划分为 k个聚类以便使得所获得的聚类满足:同一聚类中的对象相似度较高;而不同聚类中的对象相似度较小。聚类相似度是利用各聚类中对象的均值所获得一个“中心对象”(引力中心)来进行计算的。
k-means 算法的工作过程说明如下:首先从n个数据对象任意选择 k 个对象作为初始聚类中心;而对于所剩下其它对象,则根据它们与这些聚类中心的相似度(距离),分别将它们分配给与其最相似的(聚类中心所代表的)聚类;然后再计算每个所获新聚类的聚类中心(该聚类中所有对象的均值);不断重复这一过程直到标准测度函数开始收敛为止。一般都采用均方差作为标准测度函数. k个聚类具有以下特点:各聚类本身尽可能的紧凑,而各聚类之间尽可能的分开。
算法的时间复杂度上界为O(n*k*t), 其中t是迭代次数。
k-means算法是一种基于样本间相似性度量的间接聚类方法,属于非监督学习方法。此算法以k为参数,把n 个对象分为k个簇,以使簇内具有较高的相似度,而且簇间的相似度较低。相似度的计算根据一个簇中对象的平均值(被看作簇的重心)来进行。此算法首先随机选择k个对象,每个对象代表一个聚类的质心。对于其余的每一个对象,根据该对象与各聚类质心之间的距离,把它分配到与之最相似的聚类中。然后,计算每个聚类的新质心。重复上述过程,直到准则函数收敛。k-means算法是一种较典型的逐点修改迭代的动态聚类算法,其要点是以误差平方和为准则函数。逐点修改类中心:一个象元样本按某一原则,归属于某一组类后,就要重新计算这个组类的均值,并且以新的均值作为凝聚中心点进行下一次象元素聚类;逐批修改类中心:在全部象元样本按某一组的类中心分类之后,再计算修改各类的均值,作为下一次分类的凝聚中心点。
1 # coding:utf-8 2 import numpy as np 3 import matplotlib.pyplot as plt 4 5 def dis(x, y): #计算距离 6 return np.sum(np.power(y - x, 2)) 7 8 def dataN(length,k):#生成数据 9 z=range(k) 10 c=[5]*length 11 a1= [np.sin(i*2*np.pi/k) for i in range(k)] 12 a2= [np.cos(i*2*np.pi/k) for i in range(k)] 13 x=[[[i*j + np.random.uniform(0,5)]for i in c]for j in a1] 14 y=[[[i*j + np.random.uniform(0,5)]for i in c]for j in a2] 15 return x,y,z 16 17 def showP(x,y,z):#原始点作图 18 plt.figure(1) 19 color=['or', 'ob', 'og', 'ok', '^r', '+r', 'sr', 'dr', '<r', 'pr'] 20 for j in z: 21 for i in xrange(length): 22 plt.plot(x[j][i], y[j][i],color[j]) 23 24 def initCentroids(dataSet, k):#初始化中心点 25 n, d = dataSet.shape 26 centroids = np.zeros((k, d)) 27 for i in range(k): 28 index = int(np.random.uniform(0, n)) 29 centroids[i] = dataSet[index] 30 return centroids 31 32 def kmeans(dataSet, k): #kmeans算法 33 n = dataSet.shape[0] 34 clusterAssment = np.mat(np.zeros((n, 2))) 35 clusterChanged = True 36 centroids = initCentroids(dataSet, k) 37 while clusterChanged: 38 clusterChanged = False 39 for i in xrange(n): 40 distance=[[dis(centroids[j], dataSet[i])] for j in range(k)] 41 minDist= min(distance) 42 minIndex=distance.index(minDist) 43 if clusterAssment[i, 0] != minIndex: 44 clusterChanged = True 45 clusterAssment[i] = minIndex, minDist[0] 46 for j in range(k): 47 pointsInCluster = dataSet[np.nonzero(clusterAssment[:, 0]== j)[0]] 48 centroids[j] = np.mean(pointsInCluster, axis = 0) 49 return centroids, clusterAssment 50 51 def showCluster(dataSet, k, centroids, clusterAssment):#结果作图 52 plt.figure(2) 53 n=len(dataSet) 54 mark = ['or', 'ob', 'og', 'ok', '^r', '+r', 'sr', 'dr', '<r', 'pr'] 55 for i in xrange(n): 56 markIndex = int(clusterAssment[i, 0]) 57 plt.plot(dataSet[i, 0], dataSet[i, 1], mark[markIndex]) 58 mark = ['Dr', 'Db', 'Dg', 'Dk', '^b', '+b', 'sb', 'db', '<b', 'pb'] 59 for i in range(k): 60 plt.plot(centroids[i, 0], centroids[i, 1], mark[i], markersize =8) 61 plt.show() 62 63 length=200 64 k=8 #k<=8 65 x,y,z=dataN(length,k) 66 showP(x,y,z) 67 68 dataSet=np.mat(zip(np.reshape(x,(1,length*k))[0],np.reshape(y,(1,length*k))[0])) 69 centroids, clusterAssment = kmeans(dataSet, k) 70 showCluster(dataSet, k, centroids, clusterAssment)