介绍摘自李航《统计学习方法》
决策树(decision tree)是一种基本的分类与回归方法。本章主要讨论用于分类的决策树。决策树模型呈树形结构,在分类问题中,表示基于特征对实例进行分类的过程。它可以认为是if-then规则的集合,也可以认为是定义在特征空间与类空间上的条件概率分布。其主要优点是模型具有可读性,分类速度快。学习时,利用训练数据,根据损失函数最小化的原则建立决策树模型。预测时,对新的数据,利用决策树模型进行分类。决策树学习通常包括3个步骤:特征选择、决策树的生成和决策树的修剪。这些决策树学习的思想主要来源于由Quinlan在1986年提出的ID3算法和1993年提出的C4.5算法,以及由Breiman等人在1984年提出的CART算法。
5.1 决策树模型与学习
5.1.1 决策树模型
定义5.1(决策树) 分类决策树模型是一种描述对实例进行分类的树形结构。决策树由结点(node)和有向边(directed edge)组成。结点有两种类型:内部结点(internal node)和叶结点(leaf node)。内部结点表示一个特征或属性,叶结点表示一个类。
用决策树分类,从根结点开始,对实例的某一特征进行测试,根据测试结果,将实例分配到其子结点;这时,每一个子结点对应着该特征的一个取值。如此递归地对实例进行测试并分配,直至达到叶结点。最后将实例分到叶结点的类中。
图5.1是一个决策树的示意图。图中圆和方框分别表示内部结点和叶结点。

5.1.2 决策树与if-then规则
可以将决策树看成一个if-then规则的集合。将决策树转换成if-then规则的过程是这样的:由决策树的根结点到叶结点的每一条路径构建一条规则;路径上内部结点的特征对应着规则的条件,而叶结点的类对应着规则的结论。决策树的路径或其对应的if-then规则集合具有一个重要的性质:互斥并且完备。这就是说,每一个实例都被一条路径或一条规则所覆盖,而且只被一条路径或一条规则所覆盖。这里所谓覆盖是指实例的特征与路径上的特征一致或实例满足规则的条件。
5.3 决策树的生成
本节将介绍决策树学习的生成算法。首先介绍ID3的生成算法,然后再介绍C4.5中的生成算法。这些都是决策树学习的经典算法。
5.3.1 ID3算法
ID3算法的核心是在决策树各个结点上应用信息增益准则选择特征,递归地构建决策树。具体方法是:从根结点(root node)开始,对结点计算所有可能的特征的信息增益,选择信息增益最大的特征作为结点的特征,由该特征的不同取值建立子结点;再对子结点递归地调用以上方法,构建决策树;直到所有特征的信息增益均很小或没有特征可以选择为止。最后得到一个决策树。ID3相当于用极大似然法进行概率模型的选择。
算法5.2(ID3算法)
输入:训练数据集D,特征集A,阈值ε;
输出:决策树T。
(1)若D中所有实例属于同一类Ck,则T为单结点树,并将类Ck作为该结点的类标记,返回T;
(2)若A=Ø,则T为单结点树,并将D中实例数最大的类Ck作为该结点的类标记,返回T;
(3)否则,按算法5.1计算A中各特征对D的信息增益,选择信息增益最大的特征Ag;
(4)如果Ag的信息增益小于阈值,则置T为单结点树,并将D中实例数最大的类Ck作为该结点的类标记,返回T;
(5)否则,对Ag的每一可能值ai,依Ag=ai将D分割为若干非空子集Di,将Di中实例数最大的类作为标记,构建子结点,由结点及其子结点构成树T,返回T;
(6)对第i个子结点,以Di为训练集,以A-{Ag}为特征集,递归地调用步(1)~步(5),得到子树Ti,返回Ti。
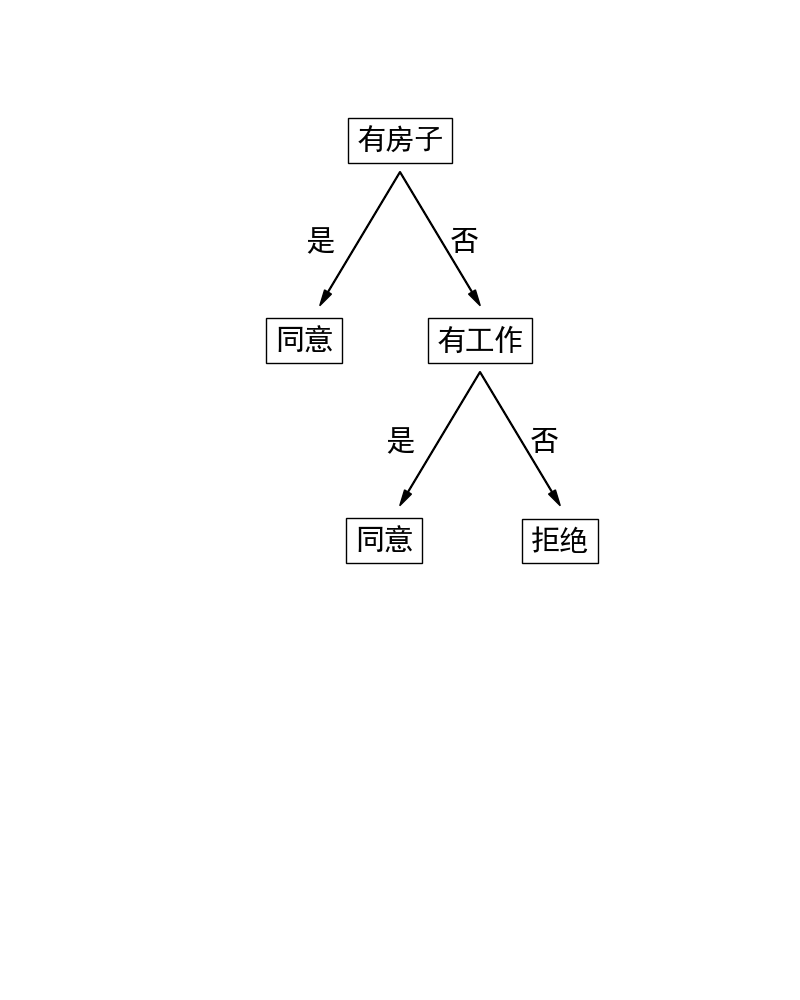
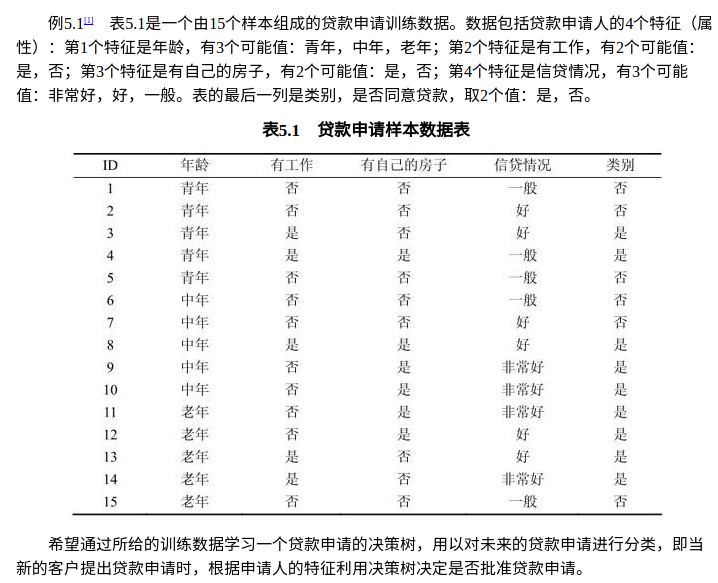
1 # coding:utf-8 2 import matplotlib.pyplot as plt 3 import numpy as np 4 import pylab 5 6 def createDataSet(): #贷款申请样本数据表 7 dataset = [["青年", "否", "否", "一般", "拒绝"], 8 ["青年", "否", "否", "好", "拒绝"], 9 ["青年", "是", "否", "好", "同意"], 10 ["青年", "是", "是", "一般", "同意"], 11 ["青年", "否", "否", "一般", "拒绝"], 12 ["中年", "否", "否", "一般", "拒绝"], 13 ["中年", "否", "否", "好", "拒绝"], 14 ["中年", "是", "是", "好", "同意"], 15 ["中年", "否", "是", "非常好", "同意"], 16 ["中年", "否", "是", "非常好", "同意"], 17 ["老年", "否", "是", "非常好", "同意"], 18 ["老年", "否", "是", "好", "同意"], 19 ["老年", "是", "否", "好", "同意"], 20 ["老年", "是", "否", "非常好", "同意"], 21 ["老年", "否", "否", "一般", "拒绝"], 22 ] 23 labels = ["年龄", "有工作", "有房子", "信贷情况"] 24 return dataset, labels 25 26 def getList(dataset,index=-1):#返回每层列表 27 alist=[i[index] for i in dataset] 28 aset=list(set(alist)) 29 acount=[alist.count(aset[j]) for j in range(len(aset))] 30 return alist,aset,acount 31 32 def getdH(account): #计算H(D) 33 t=np.sum(account) 34 return np.sum([-a*1.0/t*np.log2(a*1.0/t) for a in account]) 35 36 def getdaH(acount,ad): #计算H(D,A) 37 t=np.sum(acount) 38 return np.sum([[0 if j==0 else -a*j*1.0/t/a*np.log2(j*1.0/a) for j in b] for a,b in zip(acount,ad)]) 39 40 def getaH(dataset,index): #计算g(D,A) 41 dlist,dset,dcount= getList(dataset,-1) 42 hd=getdH(dcount) 43 alist,aset,acount=getList(dataset,index) 44 ad=[[[dlist[i] for i in range(len(dlist)) if dataset[i][index]==j].count(k) for k in dset] for j in aset] 45 return hd-getdaH(acount,ad) 46 47 def ID3(dataset,labels,tree=[]):#ID3算法 48 dlist,dset,dcount= getList(dataset,-1) 49 if len(dset)<2 : 50 tree.append(dset[0]) 51 return 52 adlist=[[getaH(dataset,i),i] for i in range(len(dataset[0])-1)] 53 t1= max(adlist,key=lambda x: x[0]) 54 tree.append(labels[t1[1]]) 55 alist,aset,acount=getList(dataset,t1[1]) 56 for a in aset: 57 tree.append(a) 58 ID3([i for i in dataset if i[t1[1]]==a],labels,tree) 59 return tree 60 61 def showT(tree):#根据Tree列表绘制图像 62 import sys 63 reload(sys) 64 sys.setdefaultencoding('utf-8') 65 pylab .mpl.rcParams['font.sans-serif'] = ['SimHei'] 66 fig1 = plt.figure(1, (8, 10)) 67 ax = fig1.add_axes([0, 0, 1, 1], frameon=False, aspect=1.) 68 m=len(tree)/2 69 n=len(tree)-1 70 xy=[[0.5+j*0.05,0.85-j*0.1] for j in range(m+1)] 71 for j in range(m): 72 if j%2!=0: 73 fig1.text(xy[j][0]+0.03,xy[j][1], tree[j],ha="center",size=21) 74 else: 75 fig1.text(xy[j][0],xy[j][1], tree[j],ha="center",size=21,bbox=dict(boxstyle="square", fc="w", ec="k")) 76 ax.arrow(xy[j][0],xy[j][1]+0.06-0.025*j, 0.09,-0.15, head_width=0.01, head_length=0.02, fc='k', ec='k') 77 fig1.text(xy[m][0],xy[m][1], tree[m],ha="center",size=21,bbox=dict(boxstyle="square", fc="w", ec="k")) 78 for j in range(m+1,n+1): 79 if j%2!=0: 80 fig1.text(xy[n-j][0]-0.15,xy[n-j][1], tree[j],ha="center",size=21) 81 else: 82 fig1.text(xy[n-j][0]-0.12,xy[n-j][1]-0.2, tree[j], 83 ha="center",size=21,bbox=dict(boxstyle="square", fc="w", ec="k")) 84 ax.arrow(xy[n-j][0],xy[n-j][1]+0.06-0.025*(n-j), -0.09,-0.15, 85 head_width=0.01, head_length=0.02, fc='k', ec='k') 86 ax.xaxis.set_visible(False) 87 ax.yaxis.set_visible(False) 88 plt.draw() 89 plt.show() 90 91 dataset,labels=createDataSet() 92 tree= ID3(dataset,labels) #["有房子","否","有工作","否","拒绝","是","同意","是","同意"] 93 showT(tree)