1.经典汉诺塔问题:大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定,任何时候,在小圆盘上都不能放大圆盘,且在三根柱子之间一次只能移动一个圆盘。问应该如何操作?
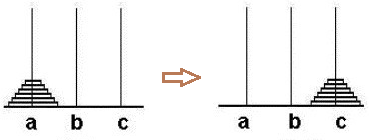
在这个问题中,我们可以先分为两步,首先将上面63个盘子看做一个整体借助c柱移动到b柱,然后将最下面的大圆盘移到c柱;然后将63个圆盘再次分为两步移动,第一步将上面的62个盘子借助c柱移到a柱,第二步将剩余的一个大圆盘移到c柱;后面的依次类推。。。。
附上代码如下:
public static int process(int num,String a,String b,String c){ if(num == 0){ return 0; } if(num == 1){ System.out.println("Move 1 from "+a+" to "+c); return 1; } int part1=process(num-1,a,c,b); int part2=1; System.out.println("Move "+num+" from "+a+" to "+c); int part3=process(num-1,b,a,c); return part1+part2+part3; }
当移动三个圆盘时的结果如下:

2.汉诺塔问题升级版:在经典汉诺塔问题基础新增一个要求,要求每次移动一个圆盘都需要经过中间的一个圆柱(B柱),求出每次移动的步骤及最少移动次数。
当只剩最上一层需要移动时,则有如下处理:
当由A柱移动到B柱时打印“Move 1 from A to B”;当由B柱移动到A柱时打印“Move 1 from B to A”;当由B柱移动到C柱时打印“Move 1 from B to C”;当由C柱移动到B柱时打印“Move 1 from C to B”;当由A柱移动到C柱时打印“Move 1 from A to B”和“Move 1 from B to C”;当由C柱移动到A柱时打印“Move 1 from C to B”和“Move 1 from B to A”。
以上也是递归的终止条件。
下面对有N层圆盘需要移动时的分析:
(1)当将N层圆盘都由A柱移动到B柱时可以分如下三步:
a.将上面N-1个圆盘由A柱移动到C柱
b.将最小面的第N个圆盘由A柱移动到B柱
c.将上面的N-1个圆盘由C柱移动到B柱
(2)当将N层圆盘都由B柱移动到A柱或者由B柱移动到C柱或者由C柱移动到B柱这三种情况与上面的由A柱移动到B柱情况相同。
(3)当将N层圆盘都由A柱移动到C柱(或者都由C柱移动到A时) 分如下五个步骤:
a.将N-1个圆盘都由A柱移动到C柱;
b.将第N个圆盘由A柱移动到B柱;
c.将N-1个圆盘由C柱移动到A柱;
d.将第N个圆盘由B柱移动到C柱;
e.将N-1个圆盘由A柱移动到C柱;
附上代码如下:
public static int process(int num,String a,String b,String c,String from,String to){ if(num == 0){ return 0; } if(num == 1){ if(from.equals(b)||to.equals(b)){ System.out.println("Move 1 from "+from+" to "+to); return 1; }else{ System.out.println("Move 1 from "+from+" to "+b); System.out.println("Move 1 from "+b+" to "+to); return 2; } } if(from.equals(b)||to.equals(b)){ String helpTemp=(to.equals(c)||from.equals(c))?a:c; int part1=process(num-1,a,b,c,from,helpTemp); int part2=1; int part3=process(num-1,a,b,c,helpTemp,to); return part1+part2+part3; }else{ int part1=process(num-1,a,b,c,from,to); System.out.println("Move "+num+" from "+from+" to "+b); int part2=1; int part3=process(num-1,a,b,c,to,from); System.out.println("Move "+num+" from "+b+" to "+to); int part4=1; int part5=process(num-1,a,b,c,from,to); return part1+part2+part3+part4+part5; } }
当移动圆盘个数为2时结果如下:
Move 1 from A to B Move 1 from B to C Move 2 from A to B Move 1 from C to B Move 1 from B to A Move 2 from B to C Move 1 from A to B Move 1 from B to C 8
