一、统计描述指标的选择与应用
计量资料：集中趋势与离散趋势
（1）正态分布：均数标准差
（2）非正态分布（偏态、不规则分布）：中位数（M），四分位数 （P25、P75）
无序分类资料：率、构成比
二、集中趋势与离散趋势
集中趋势：用平均数（指标体系）反映一组观察值的中心位置或平均水平。
（1）算数均数 — 正态分布/单峰对称分布资料
（2）中位数 — 偏态分布、不规则分布、开口资料
（3）几何均数 — 抗体滴度等各变量之间成倍数关系/对数正态分布资料
离散趋势：
（1）标准差、方差— 正态分布/单峰对称分布资料
（2）四分位数间距— 偏态分布、不规则分布、开口资料
（3）极差（全距）：最大值与最小值之差
（4）变异系数 — 度量衡单位不同、均数相差悬殊的几组资料间的比较
三、相对离散度
对于单位不同的变量，不能直接比较标准差，如身高的标准差与体重的标准差没有可比性，此时用
变异系数 (coefficient of variation, CV)来衡量。
变异系数 (coefficient of variation, CV)指标准差与均数之比，常用百分位数表示。
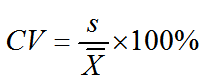CV=标准差/均数*100%
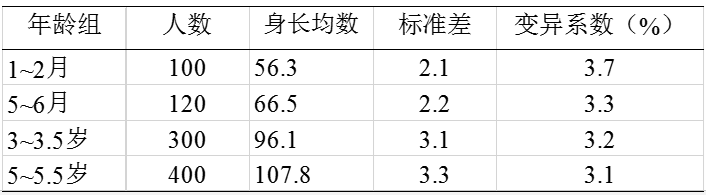
另外一个应用场景：均数相差悬殊的几组资料间的比较。
