题目链接:https://www.luogu.com.cn/problem/P1002
题目大意
棋盘上(A)点有一个过河卒,需要走到目标(B)点。卒行走的规则:可以向下、或者向右。同时在棋盘上CC点有一个对方的马,该马所在的点和所有跳跃一步可达的点称为对方马的控制点。因此称之为“马拦过河卒”。
棋盘用坐标表示,(A)点((0, 0))、(B)点((n, m))((n), (m)为不超过(20)的整数),同样马的位置坐标是需要给出的。
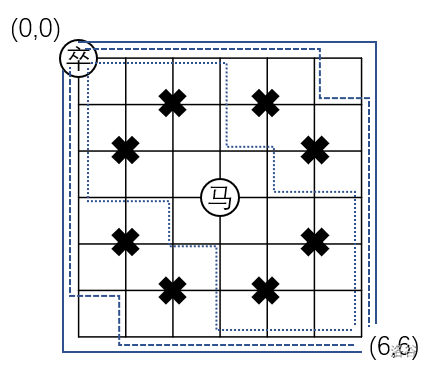
现在要求你计算出卒从(A)点能够到达(B)点的路径的条数,假设马的位置是固定不动的,并不是卒走一步马走一步。
输入格式
一行四个数据,分别表示(B)点坐标和马的坐标。
输出格式
一个数据,表示所有的路径条数。
样例输入1
6 6 3 3
样例输出1
6
题解
首先,不难看出,这是一道 动态规划 问题。
我们可以令 (f[i][j]) 表示从 ((0,0))(左上方的点)走到 ((i,j)) (第(i)行第(j)列)的方案数。
那么,在不考虑马的存在的时候,可以得到状态转移方程如下:
- 如果 (i=0) 且 (j=0) ,则 (f[i][j] = 1);
- 否则,如果 (i=0) ,则 (f[i][j] = f[i][j-1]);
- 否则,如果 (j=0) ,则 (f[i][j] = f[i-1][j]);
- 否则,(f[i][j] = f[i-1][j] + f[i][j-1])。
但是,这里有马的存在,左移在上述条件的基础上,我们必须先进行一步判断(并且这一步判断还是必须放在最前面的):
- 如果 ((i,j)) 处于马的公鸡范围内,则 (f[i][j] = 0)。
实现代码如下:
#include <bits/stdc++.h>
using namespace std;
int n, m, x, y;
long long f[22][22];
int main() {
cin >> n >> m >> x >> y;
for (int i = 0; i <= n; i ++) {
for (int j = 0; j <= m; j ++) {
if (abs(x-i)==2 && abs(y-j)==1 || abs(x-i)==1 && abs(y-j)==2 || x==i && y==j) f[i][j] = 0;
else if (i==0 && j==0) f[i][j] = 1;
else if (i==0) f[i][j] = f[i][j-1];
else if (j==0) f[i][j] = f[i-1][j];
else f[i][j] = f[i-1][j] + f[i][j-1];
}
}
cout << f[n][m] << endl;
return 0;
}