巴卡尔

【题目背景】

“爆龙王”巴卡尔是群龙之王，刚进入魔界时，他曾凭强大而神秘的力量被任命为第九使徒。战败的巴卡尔利用寂静城从魔界逃离到新的世界——天界。面对一个从未被魔界人发现的天界，巴卡尔为了削弱天族的反抗，利用自己的魔法部队做前锋，开始一步一步地对天界进行统治。

然而，恐怖如斯的巴卡尔在Justpenzi233一到天界的时候就抓住了他。

不巧，巴卡尔还特别喜欢……看足球。

【问题描述】

巴卡尔看的这场天界杯举办的尤其劣质，他希望你能解决这个问题。

一共有n支球队参加这场比赛，每支球队都有一个取值在 1~2³⁰-1 之间的整数编号。

足球锦标赛是一个淘汰赛制的比赛——每场比赛过后，你要选择一支球队淘汰，淘汰了的球队将不能再参加比赛。锦标赛在只有一支球队留下的时候就结束了。

巴卡尔告诉了你一个神奇的规律：在任意一场比赛中，这场比赛的得分是参加比赛两队的编号的异或(Xor)值。例如：12 编号为的队伍和编号为 20 的队伍之间的比赛的得分是 24 分，因为

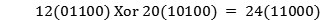
你需要安排一个比赛顺序，使得所有比赛的得分和最高。

【输入格式】

第一行一个正整数 n , 代表球队的数量。

接下来 n 行，第 i 行 1 个正整数，代表第 i 支球队的编号。

【输出格式】

一行一个非负整数，表示所有比赛得分之和的最大值。

【样例输入】

4

3

6

7

10

【样例输出】

34

【数据规模与约定】

对于30%的数据，n<=5

对于60%的数据，n<=100

对于100%的数据，n<=2000

---

 思路：

简单粗暴，容易发现这个题就是求个最大生成树，两点间的边权等于编号的异或值，用Kruskal或者Prim算法都能通过此题。

时间复杂度O(n log n)。

代码^-^

#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;
const int MX=2001;
bool vis[MX];
long long a[MX],dis[MX],arr[MX][MX],n,cnt,ans;

void prime()
{
    memset(dis,-1,sizeof(dis));
    dis[1]=0;
    for(int i=1;i<=n;++i)
    {
        int pos=0;
        for(int j=1;j<=n;++j) 
            if(!vis[j] && dis[j]>=dis[pos]) pos=j;
        vis[pos]=1;ans+=dis[pos];
        for(int j=1;j<=n;++j) 
        {
            dis[j]=max(dis[j],arr[pos][j]);
        }
    }
}


int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;++i)
        scanf("%d",&a[i]);
    for(int i=1;i<=n;++i) 
        for(int j=1;j<=n;++j)
        if(i!=j)
            arr[i][j]=a[i]^a[j];
    
    prime();
    printf("%lld",ans);    
    return 0;
}
/* 
4 3 6 7 10
*/