序列操作
单点加,前缀和查询:
树状数组直接维护即可。
区间加,单点查询:
设原数组为 $a[i]$ ,并更新一个数组 $c[i]$ $=$ $a[i]$ $-$ $a[i$ $-$ $1]$即为差分数组;
每次区间 $(l,$ $r)$ $+$ $x$ 直接$c[l]$ $+$ $x$,c[r + 1] - x即可;
最后求第i个数的答案就是 $∑$ $c[i]$。
区间加,前缀和查询:
设原数组为a[i],同样
树链加,单点查询(处理节点):
用树上差分进行解决;
设 $d[i]$ 表示第 $i$ 个节点到根节点 $root$ 的修改量,只记录修改量,相当于树的差分数组;
假设将 $u$ 到 $v$ 的路径上的点都加上 $a$,并且满足条件 $u$ 是 $v$ 的祖先或 $v$ 是 $u$ 的祖先,那么便可以像正常差分一样 $d[u]$ $+=$ $a$,$d[fa[v]]$ $-=$ $a$。
对于更新一个不一定有祖先关系的树链 $(u,$ $v)$ ,即希望将 $u$ 到 $v$ 的路径上都加上 $a$ ,怎么求呢?
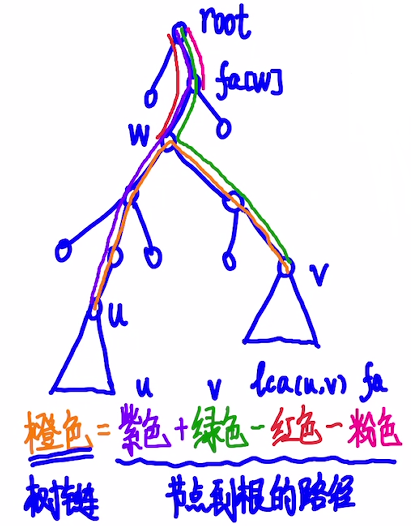
如图所示,希望更改路径 $(u,$ $v)$ 上的点权,那么只需进行一下操作:
- $d[u]$ $+=$ $a$;
- $d[v]$ $+=$ $a$;
- $d[lca(u,$ $v)]$ $-=$ $a$;
- $d[fa[lca(u,$ $v)]]$ $-=$ $a$;
证明图中可以很清晰的看出来。
如果要查询一个点的修改量,那么很容易得出这个点的修改量就是它的子树的 $d[i]$ 之和,树状数组直接维护即可(转化成 $dfs$ 序)。
如果要查询一个子树的修改量之和,那么就是 $∑$ $∑$ $d[j]$ (其中 $j$ 是 $i$ 的子孙, $i$ 是当前查询的子树的根 $u$ 的子孙);
经过化简后可以得出就是 $∑$ $d[i]$ $*$ $(depth[i]$ $-$ $depth[u]$ $+$ $1)$ (其中 $i$ 是 $u$ 的子孙, $depth[i]$ 表示 $i$ 的深度);
再进行转化后可以得出就是 $(∑$ $d[i]$ $*$ $depth[i])$ $-$ $((depth[u]$ $-$ $1)$ $*$ $(∑$ $d[i]))$;
然后用树状数组维护 $∑$ $d[i]$ $*$ $depth[i]$ 和 $∑$ $d[i]$ 即可。