凸多边形:任意两个顶点的连线都在多边形内部,这样的多边形称为凸多边形
凸包的定义:一个凸多边形的顶点的集合
求凸包的一般形式:给出一个点集,求出覆盖所有点的最小凸多边形
Graham算法:
时间复杂度:O(nlogn)极角排序耗时
先取出一个端点,必须为凸包上的一个点,取最下且最右的点即可
以端点进行极角排序,利用叉积的性质,按顺/逆时针排序,同一线上的点从远到近排
以下以顺时针排序为例进行Graham排序:
先将前两个端点入栈,后续端点按如下判断,如果栈顶两个点和下一个点顺时针排列,则入栈并继续;如果不是则将栈顶元素出栈,直到最后顺时针排列,将下一个点入栈,最后存在栈里的点就是凸包的集合。
多边形面积(不限凹凸):
已知任意一个n边形都能分解为(n-2)个三角形,然而该算法既低效,又难以实现。
计算几何当然是越抽象的算法越出色,计算所有相邻边的叉积之和的绝对值,再除二,即为多边形面积。
这里涉及到叉积的几何意义,叉积的值可以认为是由两条边形成的平行四边形面积,当然这个面积是存在正负的(在凹多边形中),实际画图示例的话,发现正负抵消恰好就是多边形面积。
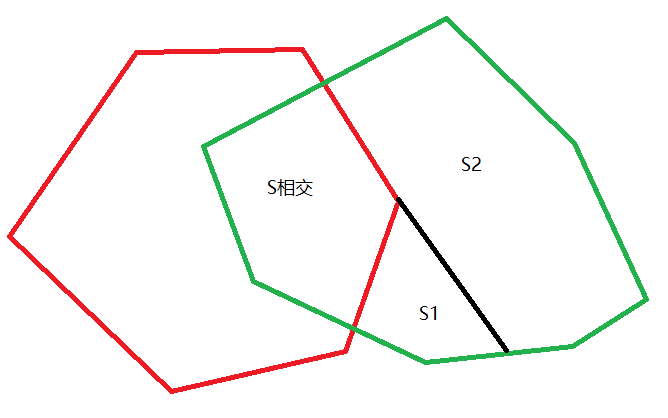
多边形相交求相交面积:
求出多边形的交点,这是一个比较容易的过程,然后我们的思路可以分为两类:
1.求相交多边形的点集,再求面积
2.求出某个多边形不与另一个多变形相交部分的面积
自己还没有做过这样的题,发现很多人都是说用2做,等以后用两个思路分别试一试看。
稳定凸包:
如果一个凸包加入一个新的点就能形成一个比原来大,并且经过原来所有点的凸包,就是稳定凸包。
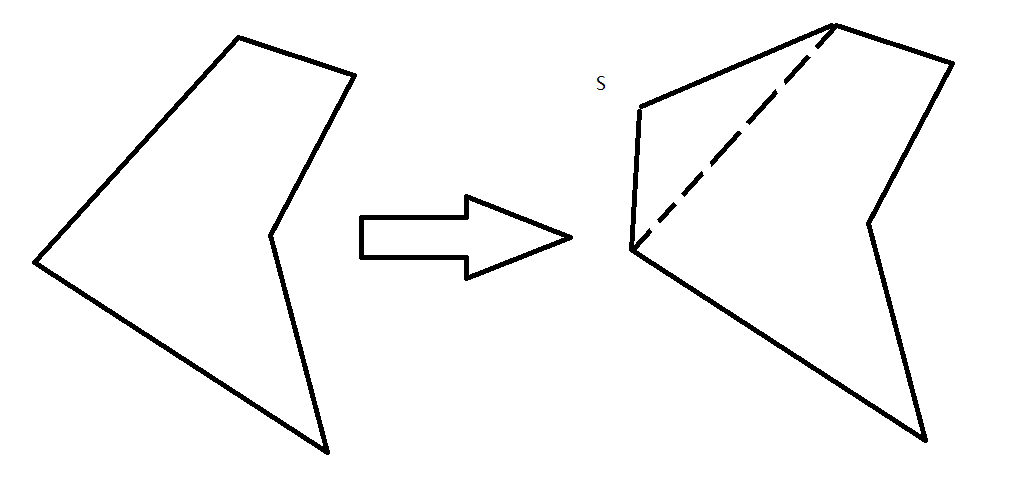
所以稳定凸包就是每条边上都至少有三个点的凸包。