scipy 最优解

参数设置：
c：线性目标函数的系数

数据类型：一维数组
A_ub（可选参数）：不等式约束矩阵，A u b A_{ub}A
ub
​ 的每一行指定x xx上的线性不等式约束的系数

数据类型：二维数组
b_ub（可选参数）：不等式约束向量，每个元素代表A u b x A_{ub}xA
ub
​ x的上限

数据类型：一维数组
A_eq（可选参数）：等式约束矩阵，A e q A_eqA
e
​ q的每一行指定x xx上的线性等式约束的系数

数据类型：二维数组
b_eq（可选参数）：等式约束向量，A e q x A_{eq}xA
eq
​ x的每个元素必须等于b e q b_{eq}b
eq
​ 的对应元素

数据类型：一维数组
bounds（可选参数）：定义决策变量x xx的最小值和最大值

数据类型： (min, max)序列对
None：使用None表示没有界限，默认情况下，界限为（0，None）（所有决策变量均为非负数）
如果提供一个元组(min, max)，则最小值和最大值将用作所有决策变量的界限。
method（可选参数）：算法，{‘interior-point’, ‘revised simplex’, ‘simplex’}以上三种算法可选

数据类型：输入如上三种字符串
callback（可选参数）：调用回调函数，我的理解是等待被调用的参数 ，如果提供了回调函数，则算法的每次迭代将至少调用一次。回调函数必须接受单个 scipy.optimize.OptimizeResult由以下字段组成：

x：当前解向量
数据类型：一维数组
fun：目标函数的当前值（c T x c^Txc
T
x）
数据类型：浮点数
success：当算法成功完成时为 True
数据类型：布尔值
slack：不等式约束的松弛值（名义上为正值）b u b − A u b x b_{ub}-A_{ub}xb
ub
​ −A
ub
​ x
数据类型：一维数组
con：等式约束的残差（名义上为零）b e q − A e q x b_{eq}-A_{eq}xb
eq
​ −A
eq
​ x
数据类型：一维数组
phase：正在执行算法的阶段
数据类型：整数
status：表示算法退出状态的整数

数据类型：整数

0 : 优化按名义进行

1 : 达到了迭代限制

2 : 问题似乎不可行

3 : 问题似乎是不收敛

4 : 遇到数值困难

nit：当前的迭代次数

数据类型：整数
message：算法状态的字符串描述符

数据类型：字符串
options（可选参数）：求解器选项字典，所有方法都接受以下选项：

数据类型：字典

maxiter：整数，要执行的最大迭代次数

disp：布尔值，设置为True以打印收敛消息，默认值：False

autoscale：布尔值，设置为True以自动执行平衡，如果约束中的数值分开几个数量级，请考虑使用此选项，默认值：False

presolve：布尔值，设置为False可禁用自动预解析，默认值：True

rr：布尔值，设置为False可禁用自动移除冗余，默认值：True

x0（可选参数）：猜测决策变量的值，将通过优化算法进行优化。当前仅由’ revised simplex’ 方法使用此参数，并且仅当 x0 表示基本可行的解决方案时才可以使用此参数。

数据类型：一维数组
4、输出格式：
x：在满足约束的情况下将目标函数最小化的决策变量的值

数据类型：一维数组
fun：目标函数的最佳值（c T x c^Txc
T
x）

数据类型：浮点数
slack：不等式约束的松弛值（名义上为正值）b u b − A u b x b_{ub}-A_{ub}xb
ub
​ −A
ub
​ x

数据类型：一维数组
con：等式约束的残差（名义上为零）b e q − A e q x b_{eq}-A_{eq}xb
eq
​ −A
eq
​ x

数据类型：一维数组
success：当算法成功找到最佳解决方案时为 True

数据类型：布尔值
status：表示算法退出状态的整数

数据类型：整数

0 : 优化成功终止

1 : 达到了迭代限制

2 : 问题似乎不可行

3 : 问题似乎是不收敛

4 : 遇到数值困难

nit：在所有阶段中执行的迭代总数

数据类型：整数
message：算法退出状态的字符串描述符

数据类型：字符串
————————————————
版权声明：本文为CSDN博主「佐佑思维」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/weixin_45288557/article/details/109139303

import scipy
from scipy import optimize
import numpy
c = numpy.array([2,3]) #最值等式未知数系数矩阵
A_ub = numpy.array([[-1,1],[2,-2]]) #<=不等式左侧未知数系数矩阵
B_ub = numpy.array([1,1]) #<=不等式右侧常数矩阵
#A_eq = numpy.array() 等式左侧未知数系数矩阵
#B_eq = numpy.array() 等式右侧常数矩阵
x = (None,1) #未知数取值范围
y = (None,None) #未知数取值范围
res = scipy.optimize.linprog(c,A_ub,B_ub,bounds = (x,y)) #默认求解最小值，求解最大值使用-c并取结果相反数
print(res)
------------------------------------------------------------------

     con: array([], dtype=float64)
     fun: -8782081992.67068
 message: 'The algorithm terminated successfully and determined that the problem is unbounded.'
     nit: 3
   slack: array([0.89792204, 1.20415592])
  status: 3
 success: False
       x: array([-1.7564164e+09, -1.7564164e+09])

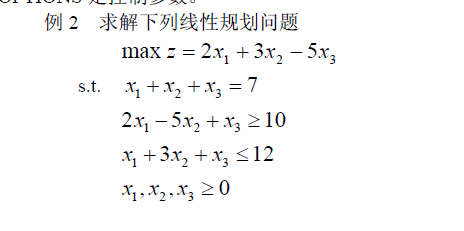
import scipy
from scipy import optimize
import numpy
c = numpy.array([2,3,-5]) #最值等式未知数系数矩阵
A_ub = numpy.array([[-2,5,-2],[1,3,1]]) #<=不等式左侧未知数系数矩阵
B_ub = numpy.array([-10,12]) #<=不等式右侧常数矩阵
#A_eq = numpy.array() 等式左侧未知数系数矩阵
#B_eq = numpy.array() 等式右侧常数矩阵
x = (0,7) #未知数取值范围
y = (0,7) #未知数取值范围
z = (0,7)
res = scipy.optimize.linprog(-c,A_ub,B_ub,[[1,1,1]],[7],bounds = (x,y,z)) #默认求解最小值，求解最大值使用-c并取结果相反数
print(res)
--------------------------------------------------------------------

 con: array([1.26250388e-08])
     fun: -14.571428538660813
 message: 'Optimization terminated successfully.'
     nit: 5
   slack: array([-3.59523238e-08,  3.85714287e+00])
  status: 0
 success: True
       x: array([6.42857141e+00, 5.71428573e-01, 1.29236762e-09])