机器学习sklearn（70）：算法实例（二十七）分类（十四）SVM（五）sklearn.svm.SVC（四） 二分类SVC的进阶

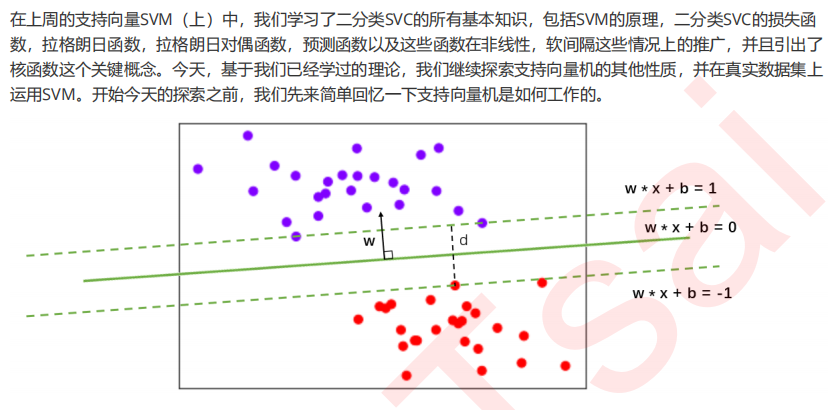
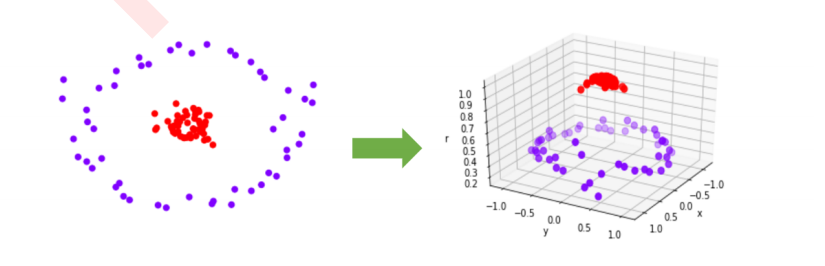
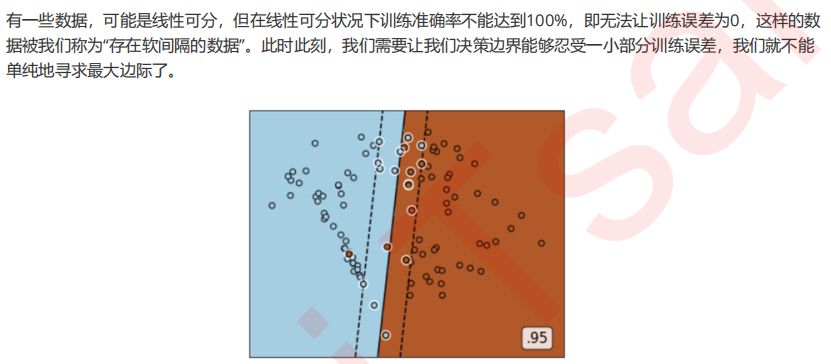
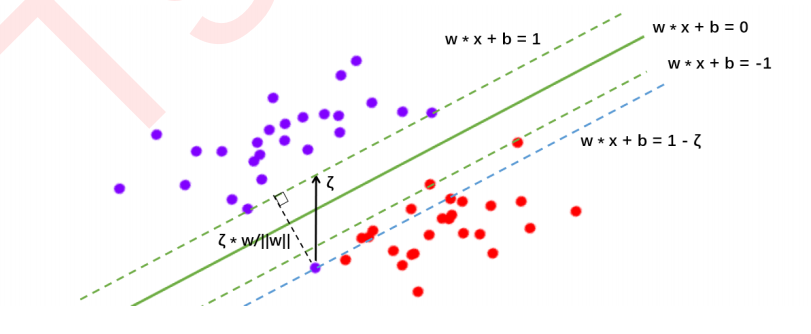
1 SVC用于二分类的原理复习

 

 

 

2 参数C的理解进阶

 

 

 

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
from sklearn import svm
from sklearn.datasets import make_circles, make_moons, make_blobs,make_classification
n_samples = 100
datasets = [
    make_moons(n_samples=n_samples, noise=0.2, random_state=0),
    make_circles(n_samples=n_samples, noise=0.2, factor=0.5, random_state=1),
    make_blobs(n_samples=n_samples, centers=2, random_state=5),
    make_classification(n_samples=n_samples,n_features = 
2,n_informative=2,n_redundant=0, random_state=5)
 ]
Kernel = ["linear"] #四个数据集分别是什么样子呢？
for X,Y in datasets:
    plt.figure(figsize=(5,4))
    plt.scatter(X[:,0],X[:,1],c=Y,s=50,cmap="rainbow")
nrows=len(datasets)
ncols=len(Kernel) + 1
fig, axes = plt.subplots(nrows, ncols,figsize=(10,16))
#第一层循环：在不同的数据集中循环
for ds_cnt, (X,Y) in enumerate(datasets):
    
    ax = axes[ds_cnt, 0]
    if ds_cnt == 0:
        ax.set_title("Input data")
    ax.scatter(X[:, 0], X[:, 1], c=Y, zorder=10, cmap=plt.cm.Paired,edgecolors='k')
    ax.set_xticks(())
    ax.set_yticks(())
    
    for est_idx, kernel in enumerate(Kernel):
        ax = axes[ds_cnt, est_idx + 1]
        
        clf = svm.SVC(kernel=kernel, gamma=2).fit(X, Y)
        score = clf.score(X, Y)
        
        ax.scatter(X[:, 0], X[:, 1], c=Y
                   ,zorder=10
                   ,cmap=plt.cm.Paired,edgecolors='k')
        ax.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1], s=100,
                    facecolors='none', zorder=10, edgecolors='white')
        
        x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
        y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
        
        XX, YY = np.mgrid[x_min:x_max:200j, y_min:y_max:200j]
        Z = clf.decision_function(np.c_[XX.ravel(), YY.ravel()]).reshape(XX.shape)
        ax.pcolormesh(XX, YY, Z > 0, cmap=plt.cm.Paired)
        ax.contour(XX, YY, Z, colors=['k', 'k', 'k'], linestyles=['--', '-', '--'],
                    levels=[-1, 0, 1])
        ax.set_xticks(())
        ax.set_yticks(())
        
        if ds_cnt == 0:
            ax.set_title(kernel)
              
        ax.text(0.95, 0.06, ('%.2f' % score).lstrip('0')
               , size=15
               , bbox=dict(boxstyle='round', alpha=0.8, facecolor='white')
               #为分数添加一个白色的格子作为底色
               , transform=ax.transAxes #确定文字所对应的坐标轴，就是ax子图的坐标轴本身
               , horizontalalignment='right' #位于坐标轴的什么方向
               )
plt.tight_layout()
plt.show()

3 二分类SVC中的样本不均衡问题：重要参数class_weight 

 

SVC的参数：class_weight 

SVC的接口fifit的参数：sample_weight

1. 导入需要的库和模块 

import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm
from sklearn.datasets import make_blobs

2. 创建样本不均衡的数据集 

class_1 = 500 #类别1有500个样本
class_2 = 50 #类别2只有50个
centers = [[0.0, 0.0], [2.0, 2.0]] #设定两个类别的中心
clusters_std = [1.5, 0.5] #设定两个类别的方差，通常来说，样本量比较大的类别会更加松散
X, y = make_blobs(n_samples=[class_1, class_2],
                  centers=centers,
                  cluster_std=clusters_std,
                  random_state=0, shuffle=False) #看看数据集长什么样
plt.scatter(X[:, 0], X[:, 1], c=y, cmap="rainbow",s=10) #其中红色点是少数类，紫色点是多数类

3. 在数据集上分别建模

#不设定class_weight
clf = svm.SVC(kernel='linear', C=1.0)
clf.fit(X, y) #设定class_weight
wclf = svm.SVC(kernel='linear', class_weight={1: 10})
wclf.fit(X, y) #给两个模型分别打分看看，这个分数是accuracy准确度
clf.score(X,y)
wclf.score(X,y)

4. 绘制两个模型下数据的决策边界

#首先要有数据分布
plt.figure(figsize=(6,5))
plt.scatter(X[:, 0], X[:, 1], c=y, cmap="rainbow",s=10)
ax = plt.gca() #获取当前的子图，如果不存在，则创建新的子图
#绘制决策边界的第一步：要有网格
xlim = ax.get_xlim()
ylim = ax.get_ylim()
xx = np.linspace(xlim[0], xlim[1], 30)
yy = np.linspace(ylim[0], ylim[1], 30)
YY, XX = np.meshgrid(yy, xx)
xy = np.vstack([XX.ravel(), YY.ravel()]).T #第二步：找出我们的样本点到决策边界的距离
Z_clf = clf.decision_function(xy).reshape(XX.shape) 
a = ax.contour(XX, YY, Z_clf, colors='black', levels=[0], alpha=0.5, linestyles=['-'])
Z_wclf = wclf.decision_function(xy).reshape(XX.shape) 
b = ax.contour(XX, YY, Z_wclf, colors='red', levels=[0], alpha=0.5, linestyles=['-'])
#第三步：画图例
plt.legend([a.collections[0], b.collections[0]], ["non weighted", "weighted"],
           loc="upper right")
plt.show()

图例这一步是怎么做到的？

a.collections #调用这个等高线对象中画的所有线，返回一个惰性对象
#用[*]把它打开试试看
[*a.collections] #返回了一个linecollection对象，其实就是我们等高线里所有的线的列表
#现在我们只有一条线，所以我们可以使用索引0来锁定这个对象
a.collections[0]
#plt.legend([对象列表],[图例列表],loc)
#只要对象列表和图例列表相对应，就可以显示出图例

从图像上可以看出，灰色是我们做样本平衡之前的决策边界。灰色线上方的点被分为一类，下方的点被分为另一类。可以看到，大约有一半少数类（红色）被分错，多数类（紫色点）几乎都被分类正确了。红色是我们做样本平衡之后的决策边界，同样是红色线上方一类，红色线下方一类。可以看到，做了样本平衡后，少数类几乎全部都被分类正确了，但是多数类有许多被分错了。我们来看看两种情况下模型的准确率如何表现： 

#给两个模型分别打分看看，这个分数是accuracy准确度
#做样本均衡之后，我们的准确率下降了，没有样本均衡的准确率更高
clf.score(X,y)
wclf.score(X,y)