(1)边长的计算公式是:
output_h =(originalSize_h+padding*2-kernelSize_h)/stride +1
输入图片大小为200×200,依次经过一层卷积(kernel size 5×5,padding 1,stride 2),pooling(kernel size 3×3,padding 0,stride 1),又一层卷积(kernel size 3×3,padding 1,stride 1)之后,输出特征图大小为:
(200-5+2*1)/2+1 为99.5,取99
(99-3)/1+1 为97
(97-3+2*1)/1+1 为97
研究过网络的话看到stride为1的时候,当kernel为 3 padding为1或者kernel为5 padding为2 一看就是卷积前后尺寸不变(卷积向下取整,池化向上取整)。
(2)如果是反卷积(deconvolution)
输入:2x2, 卷积核:4x4, 滑动步长:3, 输出:7x7
公式:2x4-(4-3)x(2-1)=8-1=7
output_w= input_w * kernerl_size - (kernel_size - stride)*(input_w - 1)
或者: (2 - 1) * 3 + 4 = 7
output = (input_w - 1) * stride + kernel_size
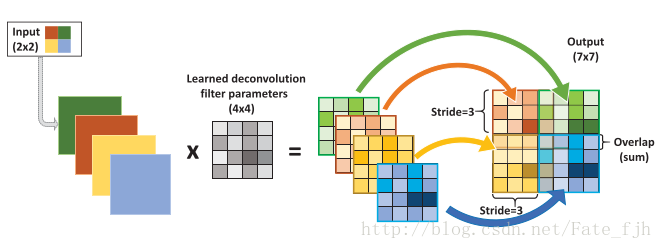
参考自 https://blog.csdn.net/qq_28424679/article/details/78665273
卷积运算和矩阵乘法的关系
考虑如下一个简单的卷积计算:
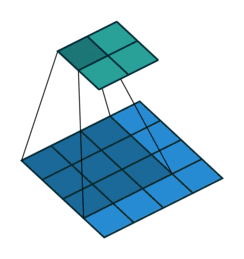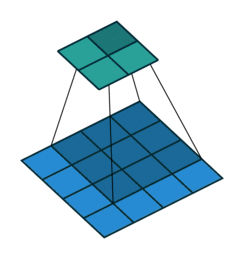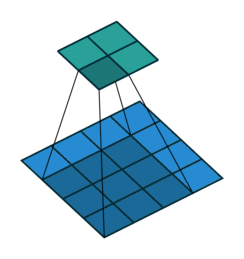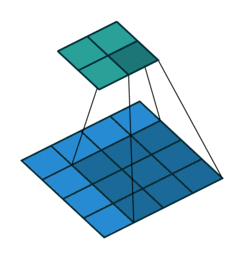
我们再把4x4的输入特征展成[16,1]的矩阵X ,那么Y = CX则是一个[4,1]的输出特征矩阵,把它重新排列2×2的输出特征就得到最终的结果,从上述分析可以看出卷积层的计算其实是可以转化成矩阵相乘的。值得注意的是,在一些深度学习网络的开源框架中并不是通过这种这个转换方法来计算卷积的,因为这个转换会存在很多无用的0乘操作。
通过上述的分析,我们已经知道卷积层的前向操作可以表示为和矩阵C相乘,那么 我们很容易得到卷积层的反向传播就是和C的转置相乘。
反卷积和卷积的关系
反卷积又被称为 转置卷积(transposed convolution),其实卷积层的前向传播过程就是反卷积层的反向传播过程,卷积层的反向传播过程就是反卷积层的前向传播过程。因为卷积层的前向反向计算分别为乘 C和C的转置,而卷积层的前向反向计算分别为成C的转置和 C转置的转置。所以它们的前向传播和反向传播刚好相反。
Fractionally Strided Convolution
反卷积也被称为 小数步长的卷积。对于步长s大于1的卷积,其对应的反卷积步长s小于1.对于反卷积的小数步长可以理解为:在其输入特征单元之间插入s-1个0,插入0后的看作新的特征输入,然后此时的步长不再是小数,而是1。因此反卷积的输入输出关系为:
o = s(i-1)+k - 2*p