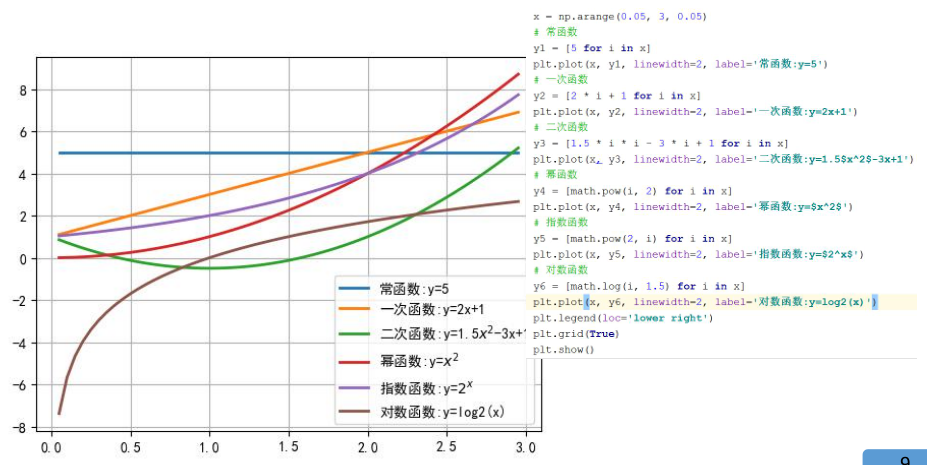
常见函数
常见函数:y=C 一次函数:y=ax+b 二次函数:y=ax^2+bx+c 幂函数y=x^a
指数函数:y=a^x,a的取值范围为:a>0&a≠1
对数函数:y=loga(x),a的取值范围为: a>0&a≠1
导数
一个函数在某一点的导数描述了这个函数在这一点附近的变化率,也可以认为是函数在某一点的导数就是该函数所代表的曲线在这一点的切线斜率。导数值越大,表示函数在该点处的变化越大。
定义:当函数y=f(x)在自变量x=x0上产生一个增量Δx时,函数输出值的增量Δy和自变量增量Δx之间的比值在Δx趋近与0的时候存在极限值a,那么a即为函数在x0处的导数值。
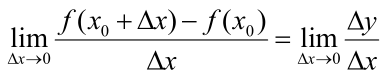
导数就是曲线的斜率,是曲线变化快慢的一个反应
二阶导数是斜率变化的反应,,表现曲线是凹凸性
y=f(x)

常见导函数

偏导数

梯度
梯度是一个向量,表示某一函数在该点处的方向导数沿着该方向取的最大值,即函数在该点处沿着该方向变化最快,变化率最大(即该梯度向量的模),当函数为一维函数的时候,梯度其实就是导数
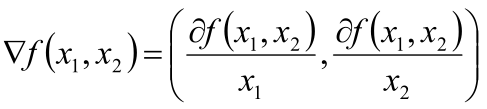
Taylor公式
Taylor(泰勒)公式是用一个函数在某点的信息描述其附近取值的公式。如果函数足够平滑,在已知函数在某一点的各阶导数值的情况下,Taylor公式可以利用这些导数值来做系数构建一个多项式近似函数在这一点的邻域中的值.
若函数f(x)在包含x0的某个闭区间[a,b]上具有n阶函数,且在开区间(a,b)上具有n+1阶函数,则对闭区间[a,b]上任意一点x,有Taylor公式如下:<f(n)(x)表示f(x)的n阶导数,Rn(x)是Taylor公式的余项,是(x-x 0)n的高阶无穷小>
古典概率
概率是以假设为基础的,即假定随机现象所发生的事件是有限的、互不相容的,而且每个基本事件发生的可能性相等。一般来讲,如果在全部可能出现的基本事件范围内构成事件A的基本事件有a个,不构成事件A的有b个,那么事件A出现的概率为:P(A)=a/a+b
概率体现的是随机事件A发生可能的大小度量(数值)
联合概率
表示两个事件共同发生的概率,事件A和事件B的共同概率记作:P(AB)、P(A,B)或者P(A∩B),读作“事件A和事件B同时发生的概率”
条件概率
事件A在另外一个事件B已经发生的条件下的发生概率叫做条件概率,表示为P(A|B),读作“在B条件下A发生的概率“,一般情况下P(A|B)≠P(A),而且条件概率具有三个特性:
非负性 P(A|B)=P(A,B)/P(B)
可列性
可加性
将条件概率公式由两个事件推广到任意有穷多个事件时,可以得到如下公式,假设A1 ,A2 ,....,An 为n个任意事件(n≥2),而且P(A1 A2 ...An )>0,则:
P(A1A2...An)=P(A1)P(A2|A1)....P(An|A1A2....An-1)
全概率公式
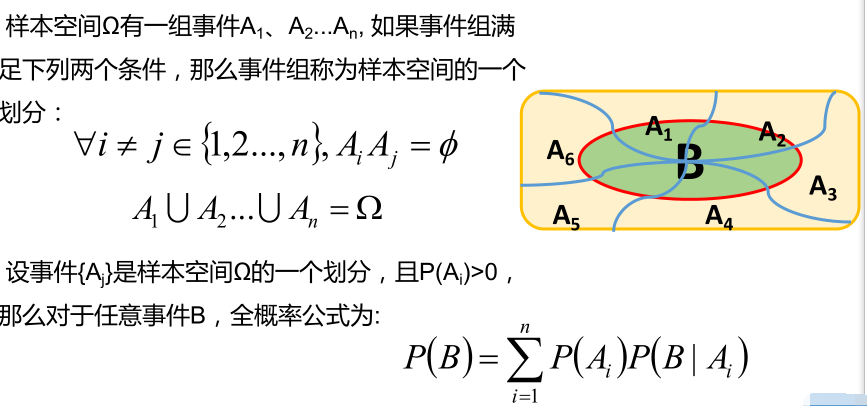
贝叶斯公式
