Hopfield网络具有最优计算功能,然而网络只能严格按照能量函数递减方式演化,很难避免伪状态的出现,且权值容易陷入局部极小值,无法收敛于全局最优解。
如果反馈神经网络的迭代过程不是那么死板,可以在一定程度上暂时接受能量函数变大的结果,就有可能跳出局部极小值。随机神经网络的核心思想就是在网络中加入概率因素,网络并不是确定的向能量函数减小的方向演化,而是以一个较大概率向这个方向演化,以保证正确的迭代方向,同时想能量函数增大的概率也存在,以防止陷入局部极小值。
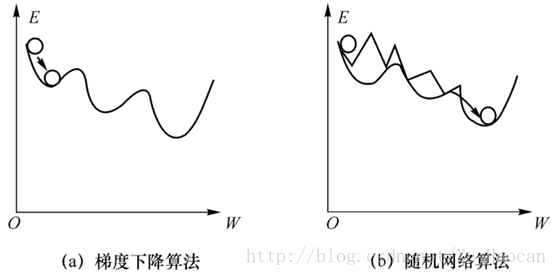
在机器学习以及优化组合问题中,最常用的方法就是梯度下降法。比如BP神经网络,多层感知器的神经元(units)越多,对应的权矩阵也就越大,每个权可视为一个自由度或者变量。我们知道自由度越高,变量越多,模型越复杂,模型的能力越强。但是模型能力越强,模型就越容易过拟合,对噪声太敏感。另一方面,使用梯度下降进行最优解搜寻时,多变量的误差曲面很像是连绵起伏的山峰一样,变量越多,山峰和山谷也越多,这就导致梯度下降法极容易陷入到局部的一个小山谷,而停止搜索(局部最优)。这就是常规的梯度下降法在解决多维度的优化问题中最常见的局部最优问题。究其原因是梯度下降法的搜索准则所致,按照梯度的负方向搜索,一味追求网络误差或能量函数的降低,使得搜索只具有“下山”的能力,而不具备“爬山”的能力。所谓“爬山”的能力,就是当搜索陷入局部最优时,还能具备一定的“翻山越岭”的能力,能够从局部最优中逃出来,继续搜索全局最优。如果为具有多个局部极小点的系统打一个形象的比喻。设想托盘上有一个凸凹不平的多维能量曲面,若在该曲面上放置一个小球,它在重力作用下,将滚入最邻近的一个低谷(局部最小点)而不能自拔。但该低谷不一定就是曲面上最低的那个低谷(全局最小点)。因此, 局部极小问题只能通过改进算法来解决 。一种可行的办法就是刚才所提到的让算法具有“爬山”的能力,同时还要保证当搜索进入全局最优时不会因为“爬山”而跑出全局最优的“山谷”。本文要讲解的随机神经网络:模拟退火(Simulated Annealing)与玻尔兹曼机(Boltzmann Machine)就是通过一定的概率保证搜索陷入局部最优时能够具有一定的“爬山”能力。这个形象的对比可参看下图:
本文先介绍模拟退火算法,然后讨论基于模拟退火算法的Boltzmann机的结构和运行原理,在介绍Sigmoid置信度网络。
模拟退火算法
模拟退火算法时非凸优化问题寻优的一种重要的启发式算法。

模拟退火算法的参数控制
为了确保模拟退火算法在有限时间收敛,必须设定控制参数控制算法收敛的参数。上面公式中,可调节的参数是控制退火快慢的参数T,T如果过大,会导致退火太慢,会延长不必要的搜索时间,T太小,则退火很快,达到局部极小值即结束迭代。实际中应该采用退火温度表,退火初期采用较大的T值,随着退火的进行,逐步降低。退火温度表包括以下内容:
- 温度的初始值T(0),初始温度应该选的够高,使得所有可能的状态转移都被接受。初始温度越高,获得高质量的解的可能性就越大,耗费时间也就越长。
- 退火速率最简单的速率下降方式有以下几种:
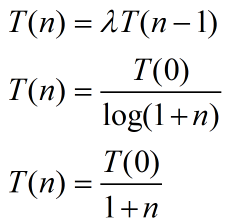
- 终止温度:如果在若干次连续的温度下没有可接受的新状态,则算法终止。
模拟退火算法的运行步骤:

Boltzmann机
G·E·Hinton等人提出一种称为 Boltzmann 机的随机神经网络 。在这种网络中神经元只有两种输出状态,即单极性二进制的0或1。状态的取值根据概率统计法则决定,由于这种概率统计法则的表达形式与著名统计力学家 L·Boltzmann 提出的 Boltzmann 分布类似,故将这种网络取Boltzmann机。
BM网络结构及运行原理

(1)BM机的结构介于DHNN全互连与BP网络的层次结构之间,形式上与单层反馈网络DHNN相似,权值对称,且wii = 0;功能上BM机与三层BP网相似,具有输入节点、输出节点和隐节点。一般把输入与输出节点称为可见节点,隐节点成为不可见节点,训练时输入输出节点收集训练样本,而隐节点主要起辅助作用,用来实现输入输出之间的联系,使得训练集能在可见单元再现。BM机的3类节点之间没有明显的层次。
(2)神经元的转移概率函数,设BM网络中单个神经元的净输入为: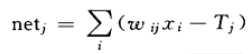
与DHNN不同的是,净输入并不能通过符号转移函数直接获得确定的输出状态,实际的输出状态将按照某种概率发生,输出某种状态的转移概率:![]()
上式表示的是神经元j输出状态取1的概率。状态为0的概率就用1减去即可。可以看出,净输入越大,神经元状态取1的概率越大;净输入越小,神经元状态取0的概率越大。而温度T的变化可改变概率曲线的形状。具体如下图所示:

从公式和图中可以看出,当温度T较高时,概率曲线变化平缓,对于同一净输入得到的状态为0或1的概率差别小;而温度低时,改率曲线陡峭,对于同一净输入状态为1或0的概率差别大;当T = 0时,概率函数退化为符号函数,神经元输出状态将无随机性。
网络能量函数与运行的搜索机制:
BM机采用的与DHNN网络相同的能量函数描述网络状态,如下图所示:
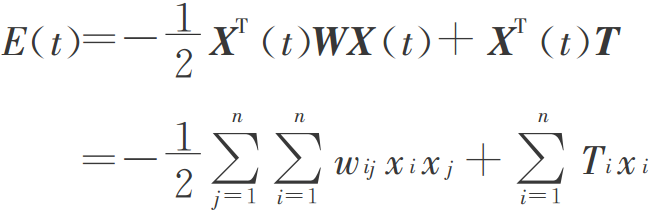
设BM机按异步方式工作,每次第j个神经元改变状态,根据能量变化公式:
![]()
下面进行进行一下讨论:
(1) 当净输入大于0时,状态为1的概率大于0.5。若原来状态xj=1,则Δxj=0,从而ΔE=0;若原理状态xj=0,则Δxj=1,从而ΔE<0,能量下降;
(2) 当净输入小于0时,状态为1的概率小于0.5。若原来状态xj=0,则Δxj=0,从而ΔE=0;若原理状态xj=1,则Δxj=-1,从而ΔE<0,能量下降;
以上对各种可能的情况讨论中可以看出,对于BM机,随着网络状态的演变,从概率意义上网络的能量总是朝着减小的方向变化。这就意味着尽管网络能量的总趋势是朝着减小的方向演进,但不排除在有些神经元状态可能会按照小概率取值,从而使网络能量暂时增加。正是因为有了这种可能性,BM机才具有了从局部极小的低谷中跳出的“爬山”能力,这一点是BM机与DHNN网能量变化的根本区别。由于采用了神经元状态按概率随机取值的工作方式,BM机的恩呢高亮具有不断跳出位置较高的低谷搜索位置较低的新低谷的能力。这种运行方式称为搜索机制,即网络在运行过程中不断地搜索更低的能量极小值,直到达到能量的全局最小。从模拟退火的原理可以看出,温度T不断下降可使得网络“爬山”能力由强减弱,这正是保证BM机能成功搜索到能量全局最小的有效措施。
BM网络的Boltzmann分布
设xj=1时对应的网络能量为E1,xj=0时网络能量为E0,根据前面的分析结果,当xj由1变为0时,有Δxj=-1,于是有如下的公式:E0-E1= ΔE = netj;对应的状态为1或状态为0的概率如下图所示:

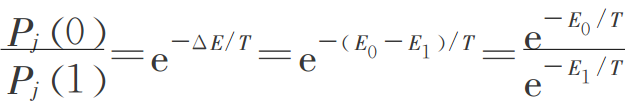
将上式推广到网络中任意两个状态出现的概率与之对应能量之间的关系,有:
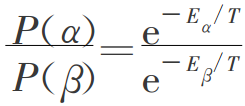
这就是著名的Boltzmann分布。从公式中可以看出:BM机处于某一状态的概率主要取决于此状态下的能量,能量越低概率越大;BM机处于某一状态的概率还取决于温度参数T,温度越高,不同状态出现的概率越近,网络能量较容易跳出局部极小而搜索全局最小,温度越低,不同状态出现的概率差别越大,网络能量较不容易改变,从而可以使得网络搜索收敛。这正是采用模拟退火方法搜索全局最小的原因所在
用BM机进行优化计算时,可构造目标函数为网络的能量函数,为防止目标函数陷入局部最优,采用上述模拟退火算法进行最优解的搜索,开始时温度设置很高,此时神经元状态为1或0概率几乎相等,因此网络能量可以达到任意可能的状态,包括局部最小或全局最小。当温度下降,不同状态的概率发生变化,能量低的状态出现的概率大,而能量高的状态出现的概率小。当温度逐渐降至0时,每个神经元要么只能取1,要么只能取0,此时网络的状态就凝固在目标函数全局最小附近。对应的网络状态就是优化问题的最优解。
用BM机进行联想时,可通过学习用网络稳定状态的概率来模拟训练样本的出现概率。根据学习类型,BM机可分为自联想和异联想。具体见最上面的Boltzmann机图。左边为自联想,右边为异联想。自联想型BM机中的可见节点V与DHNN网中的节点相似,即使输入节点也是输出节点,隐节点H的数目由学习的需要决定,而最少可以为0;异联想BM机中的可见节点V需按照功能分为输入节点组I和输出节点组O。
Boltzmann学习算法
1.学习过程:通过有导师学习,BM网络可以对训练集中各种模式的概率分布进行模拟,从而实现联想记忆。学习目的是通过调整权值使得训练集中的模式在网络状态中以相同的概率再现。学习过程可以分为两个阶段:
- 正向学习阶段或输入期:即向网络输入一对输入输出模式,将网络输入输出节点的状态钳制到期望的状态,而让隐节点自由活动以捕捉模式对之间的对应规律
- 反向学习阶段或自由活动期:对于异联想学习,钳制住输入节点而然隐含节点和输出节点自由活动;对于自联想学习,可以让其可见节点和隐节点都自由活动,已体现网络对输入输出对应规律的模拟情况。输入输出的对应规律表现为网络到达热平衡时,相连节点状态同时为一的平均概率。期望对应规律与模拟对应规律之间的差别就表现为两个学习阶段对应的平均概率的差值,此差值做为权值调整的依据。
设BM网络隐含节点个数为m,可见节点个数为n,则可见节点可表达的状态X(对于异联想,X中部分分量表示输入模式,还有一部分表示输出模式)共有2的n次方种。
设训练集共提供了P对模式,一般有P<n,训练集用一组概率缝补表示各个模式出现的概率:![]()
以上也正是在正向学习阶段期望的网络状态概率分布。当网络自由运行时,相应模式出现的概率为:
![]()


学习算法并没有学怎么懂,以后会在继续补上
Boltzmann机的运行步骤
运行是训练完成以后,根据输入数据得到输出的过程,在运行过程中权值保持不变。其运行步骤和模拟退火算法很是类似,不同之处在模拟退火算法正对不同个问题需要定义不同的代价函数,而bolzmann机的代价函数为能量函数。
(1)初始化:Boltzmann机神经元个数为N,第i个神经元与第j个神经元的连接权重为wij,初始温度为T(0),终止温度Tfinal,初始化神经元状态。
(2)在温度T(n)下,选取第i个神经元,根据下式计算输入。

如果xi>0,则能量有减小的趋势,取1为神经元i的下一个状态值,如果xi<0则按照概率选择神经元下一个状态。
(3)检查小循环的终止条件,在小循环中,使用同一个温度值T(n),如果当前状态已经达到了热平衡,则转到第(4)步进行降温,否则转到第二步,继续随机选择一个神经元选择迭代。
(4)按照指定规律降温,并检查大循环的终止条件:判断温度是否达到了终止温度,若到到终止温度则算法结束,否则转到第二步继续计算 。
初始温度T(0)的选择:可以随机选择网络中的n个神经元,取其能量的方差,或者随机选择若干神经元,取其能量的最大差值。