OpenCV形状变换

在使用OpenCV进行图像处理时，常常需要对已有的图像进行几何变换，今天我们来学习OpenCV中常用的几种基本几何变换。

1、  扩展缩放

扩展缩放只是改变图像的尺寸大小。OpenCV 提供的函数cv2.resize()可以实现这个功能。图像的尺寸可以自己手动设置，你也可以指定缩放因子。Resize()函数的定义如下：resize(src, dsize, dst=None, fx=None, fy=None, interpolation=None)。

2、  平移

平移就是将对象换一个位置。如果你要沿(x，y)方向移动，移动的距离是t_x，t_y），你可以以下面的方式构建移动矩阵：

 

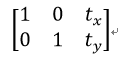
我们可以使用Numpy 数组构建这个矩阵，然后将这个矩阵传给函数cv2.warpAffine()，该函数的定义为：warpAffine(src, M, dsize, dst=None, flags=None, borderMode=None, borderValue=None)，我们只需将源图像，变换矩阵，变换后图像的大小给定，然后就可以得到经过平移后的图像了。

示例代码：

import numpy as np
import cv2 as cv
img = cv.imread('pic1.jpg',0)
rows,cols = img.shape
M = np.float32([[1,0,100],[0,1,50]])
dst = cv.warpAffine(img,M,(cols,rows))
cv.imshow('img',dst)
cv.waitKey(0)
cv.destroyAllWindows()

3、  旋转

我们先从数学推导开始，如下图所示：

 

如图所示点v 绕 原点旋转θθ 角，得到点v’，假设 v点的坐标是(x, y) ，那么可以推导得到 v’点的坐标（x’, y’)(设原点到v的距离是r，原点到v点的向量与x轴的夹角是ϕ) ：x=rcosϕ，y=rsinϕ ，x′=rcos(θ+ϕ)，y′=rsin(θ+ϕ)
通过三角函数展开得到： x′=rcosθcosϕ−rsinθsinϕ ，y′=rsinθcosϕ+rcosθsinϕ

带入x和y表达式得到：x′=xcosθ−ysinθ，y′=xsinθ +ycosθ

写成矩阵的形式是： 

 

OpenCV允许在任意位置进行旋转，此时旋转矩阵应该修改成如下形式：

 

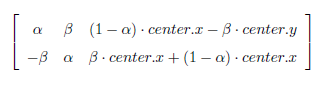
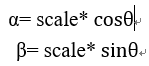
为了构建这个旋转矩阵，OpenCV 提供了一个函数cv2.getRotationMatrix2D。

下面的例子是在不缩放的情况下将图像旋转90 度。

import cv2 as cv
import numpy as np
from matplotlib import pyplot as plt

img=cv2.imread('pic1.jpg',0)
rows,cols=img.shape
# 这里的第一个参数为旋转中心，第二个为旋转角度，第三个为旋转后的缩放因子
# 可以通过设置旋转中心，缩放因子，以及窗口大小来防止旋转后超出边界的问题
M=cv2.getRotationMatrix2D((cols//2,rows//2),90,1)
# 第三个参数是输出图像的尺寸中心
dst=cv2.warpAffine(img,M,(2*cols,2*rows))
cv2.imshow('img',dst)
cv2.waitKey(0)
cv2.destroyAllWindows()

4、  仿射变换

一个任意的仿射变换都能表示为 乘以一个矩阵 (线性变换) 接着再 加上一个向量 (平移)。其实，之前我们谈论的缩放、平移以及旋转操作都可以用仿射变换来表示。经过仿射变换前后的图片可以简单地使用下图来表示：

 

假设源图片中点1的坐标为，经过放射变化后点1的坐标为，将上述变化过程用矩阵表示为：

 

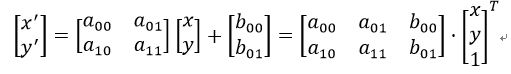
从上面公式可以看出，变换矩阵一共需要6个参数来表示，也就是一个矩阵，因此我们需要使用三个点的坐标来求解这一方程。点1, 2 和 3 (在图一中形成一个三角形) 与图二中三个点一一映射, 仍然形成三角形, 但形状已经大大改变。OpenCV给我们提供了这样的函数，只需要我们提供变换前在原图像上三个点的坐标和这三个点在变换后的图像上的坐标，cv2.getAffineTransform()函数就能够自动地计算这个变换矩阵并返回，获取变换矩阵后，再通过cv2.warpAffine()函数实施变换即可得到变换后的图像。

示例代码：

import cv2 as cv
import numpy as np
from matplotlib import pyplot as plt

img = cv.imread('pic1.jpg')
rows,cols,ch= img.shape
pts1 = np.float32([[50,50],[200,50],[50,200]])
pts2 = np.float32([[10,100],[200,50],[100,250]])
M = cv.getAffineTransform(pts1,pts2)
dst = cv.warpAffine(img,M,(cols,rows))
plt.subplot(121),plt.imshow(img),plt.title('Input')
plt.subplot(122),plt.imshow(dst),plt.title('Output')
plt.show()

5、  透视变换

对于透视变换，我们需要一个矩阵来描述变换前后的坐标关系：

 

在变换前后直线还是直线。这里w=1。要构建这个变换矩阵，你需要在输入图像上找4 个点，以及他们在输出图像上对应的位置。这四个点中的任意三个都不能共线。这个变换矩阵可以有函数cv2.getPerspectiveTransform() 构建。然后把这个矩阵传给函数cv2.warpPerspective()。

变换后的坐标为：

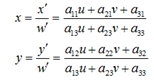
这里a₃₃=1。

示例代码：

img = cv2.imread('pic1.jpg')
rows,cols,ch = img.shape
pts1 = np.float32([[56,65],[368,52],[28,387],[389,390]])
pts2 = np.float32([[0,0],[300,0],[0,300],[300,300]])
M = cv2.getPerspectiveTransform(pts1,pts2)
dst = cv2.warpPerspective(img,M,(300,300))
plt.subplot(121),plt.imshow(img),plt.title('Input')
plt.subplot(122),plt.imshow(dst),plt.title('Output')
plt.show()