[UVA11987] Almost Union-Find

UVA11987(vjudge)

并查集神题。也是在这里头一次听说了并查集的删除操作。

题目大意：
要求支持3个操作：

1. 合并(x,y)所在集合；
2. 将(x)移到(y)所在集合；
3. 查询(x)所在集合中元素的个数和元素的和。

如果只有1、3操作，那么这道题就是一道简单的并查集。
现在有了2操作，那么就需要一点点技巧了。
众所周知并查集所产生的树结构是不定的，不一定只会是菊花图。这样就会产生问题。
比如在下面的并查集中，我们想要把4移到2所在的集合里。
但是直接移是不行的，这样4的儿子1也就到2在的集合里了。

但是，如果说将3移走的时候，在原地还留着一个3，那就不会有问题了！
或者可以这样理解，将3移走后，把装3的"盒子"留下了。
在实际实现的时候，我们会采用"虚点"的技术。
即对每个节点新建一个虚点，实点指向虚点。合并的时候用虚点操作，移动的时候操作实点。
可以用样例来实际操作一下(忽略查询操作)

1 1 2
2 3 4
1 3 5
2 4 1

首先建虚点。(带有'号的是虚点)

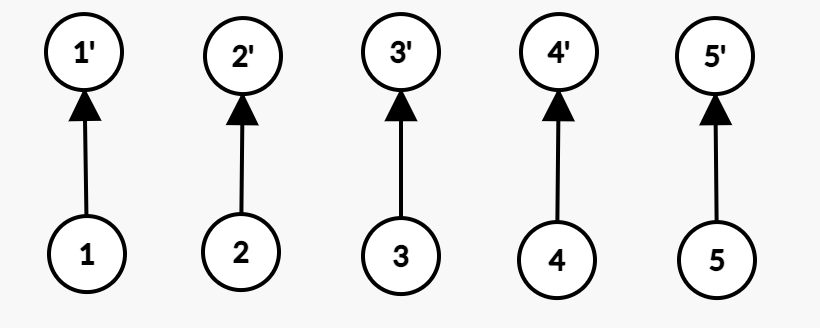
合并1、2。虚点操作。

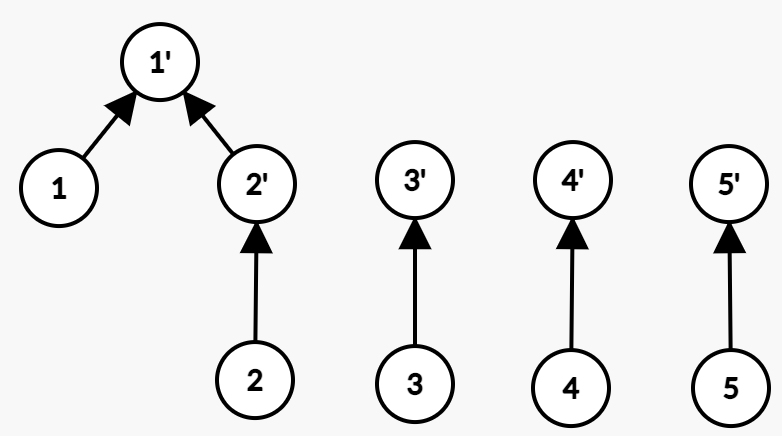
将3移到4。实点操作。

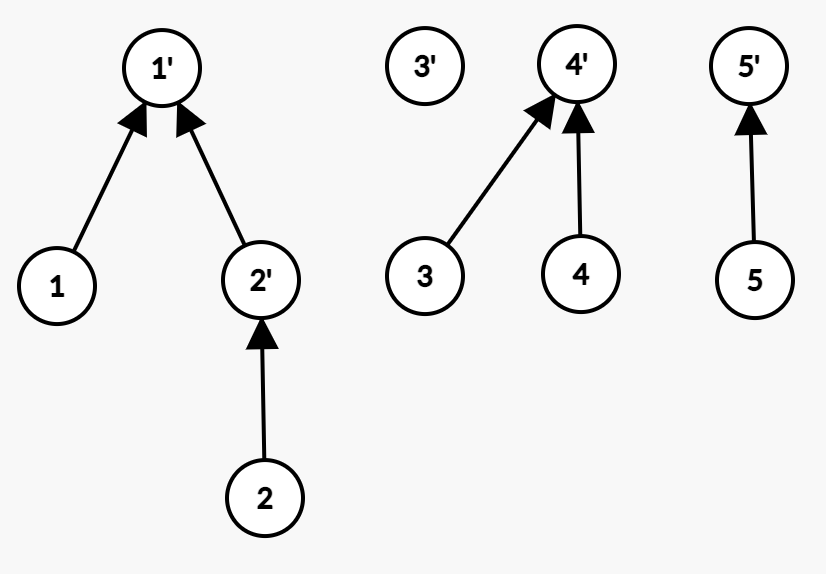
合并3、5。虚点操作。

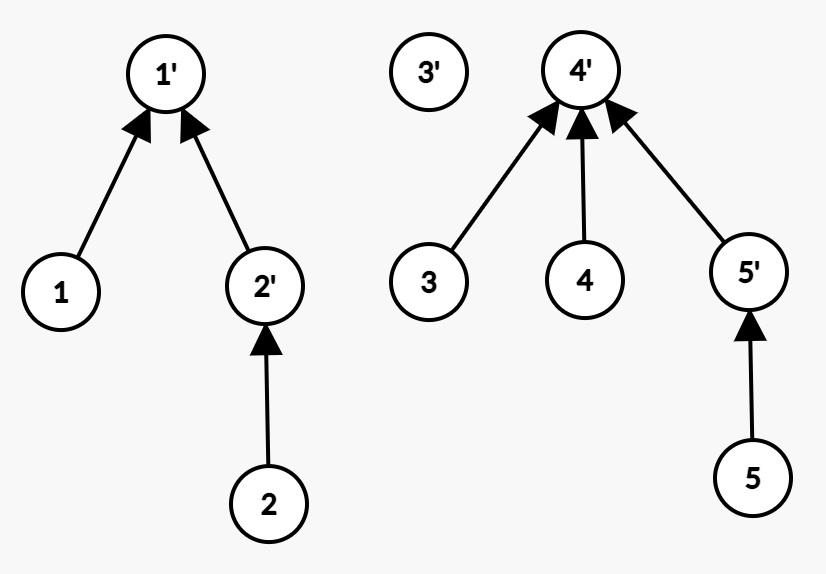
将4移到1。实点操作。

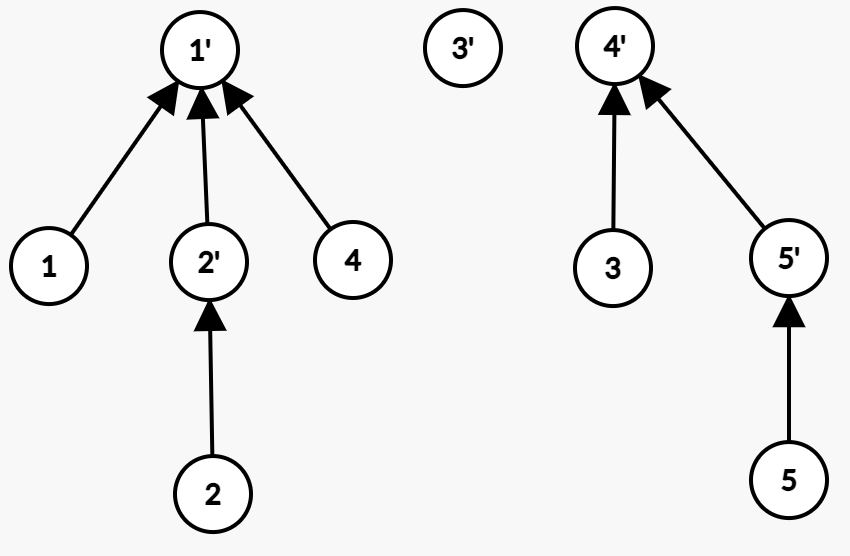
于是这道题就做完了……记得开两倍空间。

code:

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#define int long long
using namespace std;
const int maxn=100010;
int n,m,fa[maxn<<1],siz[maxn<<1],sum[maxn<<1];
void init(){for(int i=1;i<=n;i++){fa[i]=i+n;fa[i+n]=i+n;siz[i+n]=1;sum[i+n]=i;}}
int find(int xx){return fa[xx]==xx?xx:fa[xx]=find(fa[xx]);}
void merge(int xx,int yy)
{
    int fx=find(xx),fy=find(yy);
    if(fx==fy)return;
    if(siz[fx]<siz[fy]){fa[fx]=fy;siz[fy]+=siz[fx];sum[fy]+=sum[fx];}
    else{fa[fy]=fx;siz[fx]+=siz[fy];sum[fx]+=sum[fy];}
}
void move(int xx,int yy)
{
    int fx=find(xx),fy=find(yy);
    siz[fx]--;siz[fy]++;
    sum[fx]-=xx;sum[fy]+=xx;
    fa[xx]=fy;
}
void query(int xx)
{
    int fx=find(xx);
    printf("%lld %lld
",siz[fx],sum[fx]);
}
signed main()
{
    while(~scanf("%lld%lld",&n,&m))//多测警告
    {
        init();
        for(int i=1;i<=m;i++)
        {
            int opt,x,y;scanf("%lld%lld",&opt,&x);
            if(opt==1){scanf("%lld",&y);merge(x,y);}
            else if(opt==2){scanf("%lld",&y);move(x,y);}
            else{query(x);}
        }
    }
    return 0;
}