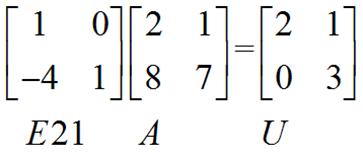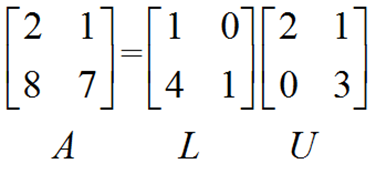线性代数(笔记四)
课程来源:网易云课堂学习计划(课程链接)
作者简述:作者为一名正在读研的学生,自己的数学状态较差。本科期间所学均能算跟得上,而且通过自己的努力经过了研究生考试。但是对数学的理解并不透彻,只是根据课上所学去做题而已。如今科研中,许多过程均需要用到所学的数学知识,然而一个好的理解和一个扎实的基础才是科研之本。数学虽然是作为一种工具,如果不了解含义,无论是是使用上还是在其基础之上进行修改均显得支支吾吾。于是决定重新学习线性代数相关知识,并做此笔记以供复习或和他人分享。
用途:此系列文章均是作者在课上所学及其自己相关的数学思想所做的笔记,如有理解错误之处还望大家指出。本系列文章均可不咨询情况下任意转载和学习(不可商用)。
作者研究方向为机器学习,如果有相同方向的小伙伴想一起学习,请加QQ123854340(备注来源博客),如果人数较多还可能建群。同时发现文章中有错误之处也请发邮件到123854340@qq.com。
在上节课中,我们介绍了矩阵乘法的五种方法。同时引出了矩阵的逆,并利用前几节课的知识对逆进行理解及求解。在这节课中,我们首先介绍求解逆矩阵的几个基本的公式,然后在消元的基础上来叙述A的LU分解。
一、逆的基本公式
在这首先介绍两个逆的基本公式,并且给出其推导方法。这样我们就可以从定义的角度进行理解,而非死记硬背。
1、由定义而来的最基本的公式AA~ = I = A~A(~为逆),这里两个矩阵的乘法可以交换顺序。
2、求矩阵A和矩阵B的乘积AB的逆矩阵。具体推导过程如下:
AB(?) = I ,我们想求解?所表示的矩阵是什么。不难看出ABB~A~ = I,由结合律可以很明显的表现出A(BB~)A~ = I,再由结合律可以看出(AB)(B~A~)= I。则由此可以得出?所表示的矩阵为B~A~。
AB的逆为B~A~,这里的乘积顺序发生了变化。在视频中教授开了一个玩笑说。这就好比穿了袜子再穿鞋的相反动作那就是得要先脱鞋再拖袜子。
3、在已知I^ = I(这里的^为转置)及(AB)^ = B^A^的条件下,求解A^的逆矩阵。推导过程如下:
AA~ = I ,两边同时进行转置操作则得出(A~)^A^ = I。很明显可以得出A^的逆矩阵为(A~)^。即(A^)~ = (A~)^。
二、A的LU分解
对于矩阵A我们可以通过一种变换将其变成矩阵U,例如对第一行进行加倍并加到第二行中的变换E21。如下矩阵所示:
在上面这个图中E21所带表的矩阵是什么呢?我们可以利用上节矩阵相乘的知识求解出E21为如下所示:
很显然我们所表示的是E21A = U,那么下面我们将对他进行变换使其成为A = LU的形式。在等式两边左侧同时乘以E21~则可以很容易得出A = E21~U,则L = E21~。A = LU的表示形式如下:
可以看出L(Lower)为下三角阵,U(Uper)为上三角阵。A的LU分解就相当于把A分解为两个三角阵的乘积形式。从消元的角度出发L为对矩阵A消元成矩阵U所做的变换的逆。下面我们将从3×3矩阵中去深刻理解这句话,并去探讨为什么存在A = LU的这种形式。
三、3×3矩阵的A = LU
在我们进行消元的过程中,我们通常去寻找一个矩阵中的主元(前几节讲过),然后利用主元对其他行进行消元。在消元十分顺利的情况下(可以进行消元且不存在因为寻找主元而更换矩阵两行的情况),我们可以将一个3×3的矩阵A消元的过程表示如下:
E32E31E21A = U ①
其所表达的意思为通过第一行的倍数对第二、三行进行消元,同时利用消元过的第二行的倍数再对第三行进行消元,使其成为一个上三角阵。很显然L矩阵可以表示为:
L = E21~E31~E32~ ②
那么一个很显然的问题来了,既然我们可以将消元表示为第①种形式,那么我们为什么还要导出其第②种形式呢?下面通过一个例子进行讲解。
这里我们首先假设E31为单位矩阵,即在用第一行对第三行进行消元过程中无需做任何变换。看如下例子:
如果将其表示为L,则由②可得如下式子:
如果第一个式子用E表示,那么我们可以看出E和L的区别。E中存在一个10,而相反L中此处却为0。之所以我们不用E去表示而选择用L是因为E的消元乘数太大。E中通过第一行的倍数对第二行进了消元,而又通过消元过的第二行的倍数对第三行进行了消元。很明显这个过程中出现了叠加,导致乘数变大。如果消元中不存在交换两行的这种变换,那么消元的乘数(E21~等)即可用来直接求解L。