先简单记下,等有时间再整理
PCA 主要思想,把 协方差矩阵 对角化,协方差矩阵是实对称的。
里面涉及到矩阵论的一点基础知识:
基变换:
Base2 = P · Base1
相应的 坐标变换
P · coordinate2 = coordinate1
将 X 转换到 Y,Y = P · X , X是原来的基,Y是新的基,P是过渡矩阵。
后面可以用 实对称阵的相似对角化来处理。
D = Y · Y^T = P(1/m·X·X^T)P^T
讲的有点乱
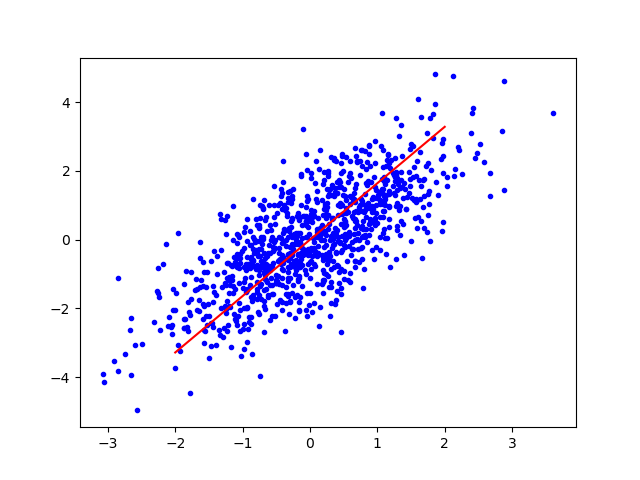
直接上代码 和图吧。
# -*- coding=utf-8 -*-
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
'''
PCA is similar diagnalization Covariance Matrix
'''
X = pd.read_csv('testSet.txt',header=None,delimiter=' ').as_matrix()
# print(X)
# 1.0centralization
# print(X.mean(axis=0)) [9.0639,9.096]
X_cen = X - X.mean(axis=0)
# 2.0 covariance matrix
cov_X = np.dot(X_cen.T,X_cen) / X_cen.shape[0]
# 3.0 get eigVector which is p A = pXX^Tp^T
# Y = p
eigVal,eigVector = np.linalg.eig(cov_X)
P = eigVector[:,::-1]
# P[:,-1] = np.array([0,0])
# Y = np.dot(P,(X_cen.T)).T
print(P)
P = np.linalg.inv(P)
'''
[-0.52045195 -0.85389096]
[-0.85389096 0.52045195]]
'''
cor = np.linspace(-2,2,1000)
plt.plot(X_cen[:,0],X_cen[:,1],'.b')
plt.plot(cor,cor*P[0,1]/P[0,0],'-r')
# plt.plot(Y[:,0],Y[:,1],'.r')
plt.show()