基础部分
递归
104. 二叉树的最大深度
简单
给定一个二叉树,找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
示例:
给定二叉树 [3,9,20,null,null,15,7],
3
/
9 20
/
15 7
返回它的最大深度 3 。
class Solution {
public int maxDepth(TreeNode root) {
if (root == null) return 0;
return 1 + Math.max(maxDepth(root.left),maxDepth(root.right));
}
}
110. 平衡二叉树
简单
给定一个二叉树,判断它是否是高度平衡的二叉树。
本题中,一棵高度平衡二叉树定义为:
一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过1。
示例 1:
给定二叉树 [3,9,20,null,null,15,7]
3
/
9 20
/
15 7
返回 true 。
示例 2:
给定二叉树 [1,2,2,3,3,null,null,4,4]
1
/
2 2
/
3 3
/
4 4
返回 false 。
class Solution {
public boolean isBalanced(TreeNode root) {
if (root == null) return true;
return Math.abs(maxDepth(root.left)-maxDepth(root.right)) <= 1 && isBalanced(root.left) && isBalanced(root.right);
}
private int maxDepth(TreeNode root) {
if (root == null) return 0;
return 1 + Math.max(maxDepth(root.left),maxDepth(root.right));
}
}
543. 二叉树的直径
简单
给定一棵二叉树,你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过也可能不穿过根结点。
示例 :
给定二叉树
1
/
2 3
/
4 5
返回 3, 它的长度是路径 [4,2,1,3] 或者 [5,2,1,3]。
注意:两结点之间的路径长度是以它们之间边的数目表示。
class Solution {
public int diameterOfBinaryTree(TreeNode root) {
if (root == null) return 0;
return Math.max(maxDepth(root.left) + maxDepth(root.right),Math.max(diameterOfBinaryTree(root.left),diameterOfBinaryTree(root.right)));
}
private int maxDepth(TreeNode root) {
if (root == null) return 0;
return 1 + Math.max(maxDepth(root.left),maxDepth(root.right));
}
}
226. 翻转二叉树
简单
翻转一棵二叉树。
示例:
输入:
4
/
2 7
/ /
1 3 6 9
输出:
4
/
7 2
/ /
9 6 3 1
class Solution {
public TreeNode invertTree(TreeNode root) {
if (root == null) return null;
TreeNode tmp = invertTree(root.left);
root.left = invertTree(root.right);
root.right = tmp;
return root;
}
}
617. 合并二叉树
简单
给定两个二叉树,想象当你将它们中的一个覆盖到另一个上时,两个二叉树的一些节点便会重叠。
你需要将他们合并为一个新的二叉树。合并的规则是如果两个节点重叠,那么将他们的值相加作为节点合并后的新值,否则不为 NULL 的节点将直接作为新二叉树的节点。
示例 1:
输入:
Tree 1 Tree 2
1 2
/ /
3 2 1 3
/
5 4 7
输出:
合并后的树:
3
/
4 5
/
5 4 7
注意: 合并必须从两个树的根节点开始。
class Solution {
public TreeNode mergeTrees(TreeNode t1, TreeNode t2) {
if (t1 == null && t2 == null) return null;
if (t1 == null) return t2;
if (t2 == null) return t1;
TreeNode root = new TreeNode();
root.val += (t1 == null ? 0 : t1.val) + (t2 == null ? 0 : t2.val);
root.left = mergeTrees(t1.left,t2.left);
root.right = mergeTrees(t1.right,t2.right);
return root;
}
}
112. 路径总和
简单
给定一个二叉树和一个目标和,判断该树中是否存在根节点到叶子节点的路径,这条路径上所有节点值相加等于目标和。
说明: 叶子节点是指没有子节点的节点。
示例:
给定如下二叉树,以及目标和 sum = 22,
5
/
4 8
/ /
11 13 4
/
7 2 1
返回 true, 因为存在目标和为 22 的根节点到叶子节点的路径 5->4->11->2。
class Solution {
public boolean hasPathSum(TreeNode root, int sum) {
if (root == null) return false;
if (root.left == null && root.right == null) return sum == root.val;
return hasPathSum(root.left,sum-root.val) || hasPathSum(root.right,sum-root.val);
}
}
437. 路径总和 III
中等
给定一个二叉树,它的每个结点都存放着一个整数值。
找出路径和等于给定数值的路径总数。
路径不需要从根节点开始,也不需要在叶子节点结束,但是路径方向必须是向下的(只能从父节点到子节点)。
二叉树不超过1000个节点,且节点数值范围是 [-1000000,1000000] 的整数。
示例:
root = [10,5,-3,3,2,null,11,3,-2,null,1], sum = 8
10
/
5 -3
/
3 2 11
/
3 -2 1
返回 3。和等于 8 的路径有:
1. 5 -> 3
2. 5 -> 2 -> 1
3. -3 -> 11
class Solution {
public int pathSum(TreeNode root, int sum) {
if (root == null) return 0;
return helper(root,sum) + pathSum(root.left, sum) + pathSum(root.right, sum);
}
private int helper(TreeNode root, int target){
if (root == null) return 0;
return (root.val == target ? 1 : 0) + helper(root.left, target-root.val) + helper(root.right, target-root.val);
}
}
572. 另一个树的子树
简单
给定两个非空二叉树 s 和 t,检验 s 中是否包含和 t 具有相同结构和节点值的子树。s 的一个子树包括 s 的一个节点和这个节点的所有子孙。s 也可以看做它自身的一棵子树。
示例 1:
给定的树 s:
3
/
4 5
/
1 2
给定的树 t:
4
/
1 2
返回 true,因为 t 与 s 的一个子树拥有相同的结构和节点值。
示例 2:
给定的树 s:
3
/
4 5
/
1 2
/
0
给定的树 t:
4
/
1 2
返回 false。
class Solution {
public boolean isSubtree(TreeNode s, TreeNode t) {
if (t == null) return true;
if (s == null) return false;
return isSameTree(s,t) || isSubtree(s.left,t) || isSubtree(s.right,t);
}
private boolean isSameTree(TreeNode s, TreeNode t){
if (s == null && t == null) return true;
if (s == null || t == null) return false;
return s.val == t.val && isSameTree(s.left,t.left) && isSameTree(s.right,t.right);
}
}
101. 对称二叉树
难度简单
给定一个二叉树,检查它是否是镜像对称的。
例如,二叉树 [1,2,2,3,4,4,3] 是对称的。
1
/
2 2
/ /
3 4 4 3
但是下面这个 [1,2,2,null,3,null,3] 则不是镜像对称的:
1
/
2 2
3 3
进阶:
你可以运用递归和迭代两种方法解决这个问题吗?
class Solution {
public boolean isSymmetric(TreeNode root) {
if (root == null || (root.left == null && root.right == null)) return true;
if (root.left == null || root.right == null) return false;
return isMirrorTree(root.left,root.right);
}
private boolean isMirrorTree(TreeNode s, TreeNode t){
if (s == null && t == null) return true;
if (s == null || t == null) return false;
return s.val == t.val && isMirrorTree(s.left,t.right) && isMirrorTree(s.right,t.left);
}
}
111. 二叉树的最小深度
简单
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明: 叶子节点是指没有子节点的节点。
示例:
给定二叉树 [3,9,20,null,null,15,7],
3
/
9 20
/
15 7
返回它的最小深度 2.
class Solution {
public int minDepth(TreeNode root) {
if (root == null) return 0;
if (root.left == null && root.right == null) return 1;
int l = root.left == null ? Integer.MAX_VALUE : minDepth(root.left);
int r = root.right == null ? Integer.MAX_VALUE : minDepth(root.right);
return 1 + Math.min(l, r);
}
}
404. 左叶子之和
简单
计算给定二叉树的所有左叶子之和。
示例:
3
/
9 20
/
15 7
在这个二叉树中,有两个左叶子,分别是 9 和 15,所以返回 24
class Solution {
public int sumOfLeftLeaves(TreeNode root) {
if (root == null) return 0;
return (root.left != null && isLeaf(root.left) ? root.left.val : 0) + sumOfLeftLeaves(root.left) + sumOfLeftLeaves(root.right);
}
private boolean isLeaf(TreeNode root){
return root.left == null && root.right == null;
}
}
687. 最长同值路径
简单
给定一个二叉树,找到最长的路径,这个路径中的每个节点具有相同值。 这条路径可以经过也可以不经过根节点。
注意:两个节点之间的路径长度由它们之间的边数表示。
示例 1:
输入:
5
/
4 5
/
1 1 5
输出:
2
示例 2:
输入:
1
/
4 5
/
4 4 5
输出:
2
注意: 给定的二叉树不超过10000个结点。 树的高度不超过1000。
class Solution {
int res = 0;
public int longestUnivaluePath(TreeNode root) {
longestPath(root);
return res;
}
private int longestPath(TreeNode root){
if (root == null) return 0;
int resOflr = 0;
int left = longestPath(root.left);
int right = longestPath(root.right);
if (root.left != null && root.val == root.left.val && root.right != null && root.right.val == root.val)
res = Math.max(left + right + 2, res); //左中右
if (root.left != null && root.val == root.left.val) //上中左
resOflr = left + 1;
if (root.right != null && root.right.val == root.val) //上中右
resOflr = Math.max(resOflr, right + 1);
res = Math.max(res, resOflr);
return resOflr;
}
}
337. 打家劫舍 III
中等
在上次打劫完一条街道之后和一圈房屋后,小偷又发现了一个新的可行窃的地区。这个地区只有一个入口,我们称之为“根”。 除了“根”之外,每栋房子有且只有一个“父“房子与之相连。一番侦察之后,聪明的小偷意识到“这个地方的所有房屋的排列类似于一棵二叉树”。 如果两个直接相连的房子在同一天晚上被打劫,房屋将自动报警。
计算在不触动警报的情况下,小偷一晚能够盗取的最高金额。
示例 1:
输入: [3,2,3,null,3,null,1]
3
/
2 3
3 1
输出: 7
解释: 小偷一晚能够盗取的最高金额 = 3 + 3 + 1 = 7.
示例 2:
输入: [3,4,5,1,3,null,1]
3
/
4 5
/
1 3 1
输出: 9
解释: 小偷一晚能够盗取的最高金额 = 4 + 5 = 9.
class Solution {
public int rob(TreeNode root) {
return helper(root, true);
}
private int helper(TreeNode root, boolean canStealRoot){
if (root == null) return 0;
if (canStealRoot) return Math.max(helper(root.left, true) + helper(root.right, true), root.val + helper(root.left, false) + helper(root.right, false));
else return helper(root.left, true) + helper(root.right, true);
}
}
671. 二叉树中第二小的节点
简单
给定一个非空特殊的二叉树,每个节点都是正数,并且每个节点的子节点数量只能为 2 或 0。如果一个节点有两个子节点的话,那么该节点的值等于两个子节点中较小的一个。
给出这样的一个二叉树,你需要输出所有节点中的第二小的值。如果第二小的值不存在的话,输出 -1 。
示例 1:
输入:
2
/
2 5
/
5 7
输出: 5
说明: 最小的值是 2 ,第二小的值是 5 。
示例 2:
输入:
2
/
2 2
输出: -1
说明: 最小的值是 2, 但是不存在第二小的值。
class Solution {
long[] res;
public int findSecondMinimumValue(TreeNode root) {
res = new long[2];
res[0] = Long.MAX_VALUE;
res[1] = Long.MAX_VALUE;
helper(root);
return res[1]==Long.MAX_VALUE ? -1 : (int) res[1];
}
private void helper(TreeNode root){
if (root.left != null) helper(root.left);
long num = (long) root.val;
if (num < res[0]){
res[1] = res[0];
res[0] = num;
}else if (num != res[0] && num < res[1]){
res[1] = num;
}
if (root.right != null) helper(root.right);
}
}
层次遍历
637. 二叉树的层平均值
简单
给定一个非空二叉树, 返回一个由每层节点平均值组成的数组。
示例 1:
输入:
3
/
9 20
/
15 7
输出:[3, 14.5, 11]
解释:
第 0 层的平均值是 3 , 第1层是 14.5 , 第2层是 11 。因此返回 [3, 14.5, 11] 。
提示:
- 节点值的范围在32位有符号整数范围内。
class Solution {
public List<Double> averageOfLevels(TreeNode root) {
List<Double> res = new LinkedList<>();
if (root == null) return res;
Queue<TreeNode> queue = new LinkedList<>();
queue.add(root);
while (!queue.isEmpty()){
int size = queue.size();
double sum = 0;
for (int i = 0; i < size; i++){
TreeNode node = queue.poll();
sum += node.val;
if (node.left != null) queue.add(node.left);
if (node.right != null) queue.add(node.right);
}
res.add(sum / size);
}
return res;
}
}
513. 找树左下角的值
中等
给定一个二叉树,在树的最后一行找到最左边的值。
示例 1:
输入:
2
/
1 3
输出:
1
示例 2:
输入:
1
/
2 3
/ /
4 5 6
/
7
输出:
7
注意: 您可以假设树(即给定的根节点)不为 NULL。
class Solution {
public int findBottomLeftValue(TreeNode root) {
Queue<TreeNode> queue = new LinkedList<>();
queue.add(root);
int res = root.val;
while (!queue.isEmpty()){
int size = queue.size();
boolean updated = false;
for (int i = 0; i < size; i++){
TreeNode node = queue.poll();
if (node.left != null) {
if (!updated){ //更新完给个标记
res = node.left.val;
updated = true;
}
queue.add(node.left);
}
if (node.right != null) {
if (!updated){
res = node.right.val;
updated = true;
}
queue.add(node.right);
}
}
}
return res;
}
}
class Solution { //从右往左遍历就完事了
public int findBottomLeftValue(TreeNode root) {
Queue<TreeNode> queue = new LinkedList<>();
queue.add(root);
while (!queue.isEmpty()) {
root = queue.poll();
if (root.right != null) queue.add(root.right);
if (root.left != null) queue.add(root.left);
}
return root.val;
}
}
前中后序遍历
144. 二叉树的前序遍历
中等
给定一个二叉树,返回它的 前序 遍历。
示例:
输入: [1,null,2,3]
1
2
/
3
输出: [1,2,3]
进阶: 递归算法很简单,你可以通过迭代算法完成吗?
class Solution { //递归
List<Integer> res = new LinkedList<>();
public List<Integer> preorderTraversal(TreeNode root) {
if (root != null) helper(root);
return res;
}
private void helper(TreeNode root){
res.add(root.val);
if (root.left != null) helper(root.left);
if (root.right != null) helper(root.right);
}
}
class Solution { //迭代
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> res = new LinkedList<>();
if (root == null) return res;
Stack<TreeNode> stack = new Stack<>();
stack.push(root);
while (!stack.isEmpty()){
TreeNode node = stack.pop();
res.add(node.val);
if (node.right != null) stack.push(node.right);
if (node.left != null) stack.push(node.left);
}
return res;
}
}
145. 二叉树的后序遍历
困难
给定一个二叉树,返回它的 后序 遍历。
示例:
输入: [1,null,2,3]
1
2
/
3
输出: [3,2,1]
进阶: 递归算法很简单,你可以通过迭代算法完成吗?
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> res = new LinkedList<>();
if (root == null) return res;
Stack<TreeNode> stack = new Stack<>();
stack.push(root);
while (!stack.isEmpty()){
TreeNode node = stack.peek();
if (node.left == null && node.right == null){
node = stack.pop();
res.add(node.val);
node = null;
continue;
}
if (node.right != null) {
stack.push(node.right);
node.right = null;
}
if (node.left != null) {
stack.push(node.left);
node.left = null;
}
}
return res;
}
}
//后序:左右中 前序先遍历右:中右左,再反过来
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
Stack<TreeNode> stack = new Stack<>();
stack.push(root);
while (!stack.isEmpty()) {
TreeNode node = stack.pop();
if (node == null) continue;
res.add(node.val);
stack.push(node.left);
stack.push(node.right);
}
Collections.reverse(res);
return res;
}
94. 二叉树的中序遍历
中等
给定一个二叉树,返回它的中序 遍历。
示例:
输入: [1,null,2,3]
1
2
/
3
输出: [1,3,2]
进阶: 递归算法很简单,你可以通过迭代算法完成吗?
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
if (root == null) return res;
Deque<TreeNode> stack = new ArrayDeque<>();
while (!stack.isEmpty() || root != null){
while (root != null){
stack.push(root);
root = root.left;
}
root = stack.pop();
res.add(root.val);
root = root.right;
}
return res;
}
}
BST
669. 修剪二叉搜索树
简单
给定一个二叉搜索树,同时给定最小边界L 和最大边界 R。通过修剪二叉搜索树,使得所有节点的值在[L, R]中 (R>=L) 。你可能需要改变树的根节点,所以结果应当返回修剪好的二叉搜索树的新的根节点。
示例 1:
输入:
1
/
0 2
L = 1
R = 2
输出:
1
2
示例 2:
输入:
3
/
0 4
2
/
1
L = 1
R = 3
输出:
3
/
2
/
1
class Solution { //迭代,磨磨唧唧,0ms
public TreeNode trimBST(TreeNode root, int L, int R) {
if (root == null) return null;
if (root.val < L) return trimBST(root.right, L, R);
if (root.val > R) return trimBST(root.left, L, R);
TreeNode p = root;
while (p != null && p.left != null){
if (p.left.val >= L){
p = p.left;
}else {
TreeNode q = p;
p = p.left;
while (p != null && p.val < L){
p = p.right;
}
q.left = p;
}
}
p = root;
while (p != null && p.right != null){
if (p.right.val <= R){
p = p.right;
}else {
TreeNode q = p;
p = p.right;
while (p != null && p.val > R){
p = p.left;
}
q.right = p;
}
}
return root;
}
}
class Solution { //递归
public TreeNode trimBST(TreeNode root, int L, int R) {
if (root == null) return null;
if (root.val < L) return trimBST(root.right, L, R);
if (root.val > R) return trimBST(root.left, L, R);
TreeNode left = trimBST(root.left, L, R);
TreeNode right = trimBST(root.right, L, R);
root.left = left;
root.right = right;
return root;
}
}
230. 二叉搜索树中第K小的元素
中等
给定一个二叉搜索树,编写一个函数 kthSmallest 来查找其中第 k 个最小的元素。
说明:
你可以假设 k 总是有效的,1 ≤ k ≤ 二叉搜索树元素个数。
示例 1:
输入: root = [3,1,4,null,2], k = 1
3
/
1 4
2
输出: 1
示例 2:
输入: root = [5,3,6,2,4,null,null,1], k = 3
5
/
3 6
/
2 4
/
1
输出: 3
进阶:
如果二叉搜索树经常被修改(插入/删除操作)并且你需要频繁地查找第 k 小的值,你将如何优化 kthSmallest 函数?
class Solution {
int res;
int count = 0;
int k;
public int kthSmallest(TreeNode root, int k) {
this.k = k;
helper(root);
return res;
}
private void helper(TreeNode root){
if (root == null || count >= k) return;
helper(root.left);
count++;
if (count == k) res = root.val;
helper(root.right);
}
}
538. 把二叉搜索树转换为累加树
简单
给定一个二叉搜索树(Binary Search Tree),把它转换成为累加树(Greater Tree),使得每个节点的值是原来的节点值加上所有大于它的节点值之和。
例如:
输入: 原始二叉搜索树:
5
/
2 13
输出: 转换为累加树:
18
/
20 13
注意:本题和 1038: https://leetcode-cn.com/problems/binary-search-tree-to-greater-sum-tree/ 相同
class Solution {
int a = 0;
public TreeNode convertBST(TreeNode root) {
if (root == null) return null;
convertBST(root.right);
a += root.val;
root.val = a;
convertBST(root.left);
return root;
}
}
235. 二叉搜索树的最近公共祖先
简单
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
例如,给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]

示例 1:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6
解释: 节点 2 和节点 8 的最近公共祖先是 6。
示例 2:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。
说明:
- 所有节点的值都是唯一的。
- p、q 为不同节点且均存在于给定的二叉搜索树中。
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if (p.val < root.val && q.val < root.val)
return lowestCommonAncestor(root.left, p, q);
else if (p.val > root.val && q.val > root.val)
return lowestCommonAncestor(root.right, p, q);
else return root;
}
}
236. 二叉树的最近公共祖先
中等
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
例如,给定如下二叉树: root = [3,5,1,6,2,0,8,null,null,7,4]
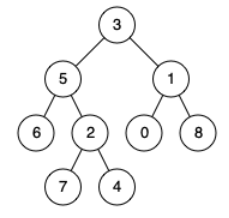
示例 1:
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出: 3
解释: 节点 5 和节点 1 的最近公共祖先是节点 3。
示例 2:
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出: 5
解释: 节点 5 和节点 4 的最近公共祖先是节点 5。因为根据定义最近公共祖先节点可以为节点本身。
说明:
- 所有节点的值都是唯一的。
- p、q 为不同节点且均存在于给定的二叉树中。
class Solution { // 递归,2452ms
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if (contain(root.left,p) && contain(root.left,q))
return lowestCommonAncestor(root.left,p,q);
if (contain(root.right,p) && contain(root.right,q))
return lowestCommonAncestor(root.right,p,q);
return root;
}
private boolean contain(TreeNode root, TreeNode p){
if (root == null) return false;
if (root.val == p.val) return true;
return contain(root.left, p) || contain(root.right, p);
}
}
class Solution { // 8ms
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if (root == null || root == p || root == q) return root;
TreeNode left = lowestCommonAncestor(root.left, p, q);
TreeNode right = lowestCommonAncestor(root.right, p, q);
if (left == null) return right;
if (right == null) return left;
return root;
}
}
108. 将有序数组转换为二叉搜索树
简单
将一个按照升序排列的有序数组,转换为一棵高度平衡二叉搜索树。
本题中,一个高度平衡二叉树是指一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1。
示例:
给定有序数组: [-10,-3,0,5,9],
一个可能的答案是:[0,-3,9,-10,null,5],它可以表示下面这个高度平衡二叉搜索树:
0
/
-3 9
/ /
-10 5
class Solution {
public TreeNode sortedArrayToBST(int[] nums) {
if (nums.length == 0) return null;
return helper(nums,0,nums.length-1);
}
private TreeNode helper(int[] nums, int low, int high){
if (low > high) return null;
int mid = low + (high - low) / 2;
TreeNode node = new TreeNode(nums[mid]);
node.left = helper(nums, low, mid-1);
node.right = helper(nums, mid+1, high);
return node;
}
}
109. 有序链表转换二叉搜索树
中等
给定一个单链表,其中的元素按升序排序,将其转换为高度平衡的二叉搜索树。
本题中,一个高度平衡二叉树是指一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1。
示例:
给定的有序链表: [-10, -3, 0, 5, 9],
一个可能的答案是:[0, -3, 9, -10, null, 5], 它可以表示下面这个高度平衡二叉搜索树:
0
/
-3 9
/ /
-10 5
class Solution { // 链表=>数组,变成上一题了,1ms
public TreeNode sortedListToBST(ListNode head) {
if (head == null) return null;
int len = 0;
ListNode p = head;
while (p != null) {
len++;
p = p.next;
}
int[] nums = new int[len];
int index = 0;
while (head != null) {
nums[index++] = head.val;
head = head.next;
}
return helper(nums, 0, len-1);
}
private TreeNode helper(int[] nums, int low, int high){
if (low > high) return null;
int mid = low + (high - low) / 2;
TreeNode node = new TreeNode(nums[mid]);
node.left = helper(nums, low, mid-1);
node.right = helper(nums, mid+1, high);
return node;
}
}
class Solution { // 2ms,List没有array快
public TreeNode sortedListToBST(ListNode head) {
if (head == null) return null;
List<Integer> list = new ArrayList<>();
while (head != null) {
list.add(head.val);
head = head.next;
}
return helper(list, 0, list.size()-1);
}
private TreeNode helper(List<Integer> list, int low, int high){
if (low > high) return null;
int mid = low + (high - low) / 2;
TreeNode node = new TreeNode(list.get(mid));
node.left = helper(list, low, mid-1);
node.right = helper(list, mid+1, high);
return node;
}
}
class Solution { // 0ms
public TreeNode sortedListToBST(ListNode head) {
if (head == null) return null;
return helper(head, null);
}
private TreeNode helper(ListNode head, ListNode tail) {
if (head == tail) return null;
// 快慢指针找中点
ListNode slow = head;
ListNode fast = head;
while (fast != tail && fast.next != tail) {
slow = slow.next;
fast = fast.next.next;
}
TreeNode root = new TreeNode(slow.val);
root.left = helper(head, slow);
root.right = helper(slow.next, tail);
return root;
}
}
653. 两数之和 IV - 输入 BST
简单
给定一个二叉搜索树和一个目标结果,如果 BST 中存在两个元素且它们的和等于给定的目标结果,则返回 true。
案例 1:
输入:
5
/
3 6
/
2 4 7
Target = 9
输出: True
案例 2:
输入:
5
/
3 6
/
2 4 7
Target = 28
输出: False
class Solution { // 3ms
HashSet<Integer> set = new HashSet<>();
public boolean findTarget(TreeNode root, int k) {
if (root == null) return false;
if (set.contains(root.val)) return true;
set.add(k-root.val);
return findTarget(root.left, k) || findTarget(root.right, k);
}
}
530. 二叉搜索树的最小绝对差
简单
给你一棵所有节点为非负值的二叉搜索树,请你计算树中任意两节点的差的绝对值的最小值。
示例:
输入:
1
3
/
2
输出:
1
解释:
最小绝对差为 1,其中 2 和 1 的差的绝对值为 1(或者 2 和 3)。
提示:
- 树中至少有 2 个节点。
- 本题与 783 https://leetcode-cn.com/problems/minimum-distance-between-bst-nodes/ 相同
class Solution {
int res = Integer.MAX_VALUE;
int restore = -1;
public int getMinimumDifference(TreeNode root) {
if (root == null) return 0;
if (root.left != null) getMinimumDifference(root.left);
if (restore == -1) restore = root.val;
else {
res = Math.min(res, root.val - restore);
restore = root.val;
}
if (root.right != null) getMinimumDifference(root.right);
return res;
}
}
501. 二叉搜索树中的众数
简单
给定一个有相同值的二叉搜索树(BST),找出 BST 中的所有众数(出现频率最高的元素)。
假定 BST 有如下定义:
- 结点左子树中所含结点的值小于等于当前结点的值
- 结点右子树中所含结点的值大于等于当前结点的值
- 左子树和右子树都是二叉搜索树
例如:
给定 BST [1,null,2,2],
1
2
/
2
返回[2].
提示:如果众数超过1个,不需考虑输出顺序
进阶:你可以不使用额外的空间吗?(假设由递归产生的隐式调用栈的开销不被计算在内)
class Solution { // 0ms
List<Integer> res = new ArrayList<>();
long restore = Long.MAX_VALUE;
int count = 0;
int maxCount = 0;
public int[] findMode(TreeNode root) {
if (root == null) return new int[]{};
helper(root);
if (count > maxCount){
res.clear();
res.add((int) restore);
}else if (count == maxCount){
res.add((int) restore);
}
int[] result = new int[res.size()];
for (int i = 0; i < result.length; i++){
result[i] = res.get(i);
}
return result;
}
private void helper(TreeNode root){
if (root == null) return;
helper(root.left);
if (root.val != restore){
if (count > maxCount){
res.clear();
res.add((int) restore);
maxCount = count;
}else if (count == maxCount){
res.add((int) restore);
}
restore = (int) root.val;
count = 1;
}else {
count++;
}
helper(root.right);
}
}
Trie
208. 实现 Trie (前缀树)
中等
实现一个 Trie (前缀树),包含 insert, search, 和 startsWith 这三个操作。
示例:
Trie trie = new Trie();
trie.insert("apple");
trie.search("apple"); // 返回 true
trie.search("app"); // 返回 false
trie.startsWith("app"); // 返回 true
trie.insert("app");
trie.search("app"); // 返回 true
说明:
- 你可以假设所有的输入都是由小写字母
a-z构成的。 - 保证所有输入均为非空字符串。
public class Trie {
public class TrieNode{
public int path;
public int end;
public HashMap<Character, TrieNode> next;
public TrieNode(){
path = 0;
end = 0;
next = new HashMap<>();
}
}
private TrieNode root;
public Trie(){
root = new TrieNode();
}
public void insert(String word){
if(word == null || word.equals("")) return ;
TrieNode node = root;
for(int i = 0; i<word.length(); i++){
char ch = word.charAt(i);
if(!node.next.containsKey(ch)) {
node.next.put(ch,new TrieNode());
}
node = node.next.get(ch);
node.path++;
}
node.end++;
}
public boolean search(String word){
if(word == null || word.equals("")) return false;
TrieNode node = root;
for(int i = 0; i<word.length(); i++){
char ch = word.charAt(i);
if(!node.next.containsKey(ch)) return false;
node = node.next.get(ch);
}
if(node.end == 0) return false;
return true;
}
public boolean startsWith(String word){
if(word == null || word.equals("")) return false;
TrieNode node = root;
for(int i = 0; i<word.length(); i++){
char ch = word.charAt(i);
if(!node.next.containsKey(ch)) return false;
node = node.next.get(ch);
}
return true;
}
}
频率排序
333,426,199,834,124,536,449,663,863,297,889,543