机器学习模型的度量选择一

作者|Alvira Swalin
编译|VK
来源|Medium

第一部分主要讨论回归度量

在后现代主义的世界里，相对主义以各种各样的形式，一直是最受欢迎和最受诟病的哲学学说之一。相对主义认为，没有普遍和客观的真理，而是每个观点都有自己的真理。

在这篇文章中，我将根据目标和我们试图解决的问题来讨论每个错误度量的用处。当有人告诉你“美国是最好的国家”时，你应该问的第一个问题是，这种说法是基于什么。我们是根据每个国家的经济状况，还是根据它们的卫生设施等来判断它们？

类似地，每个机器学习模型都试图使用不同的数据集来解决目标不同的问题，因此，在选择度量标准之前了解背景是很重要的。

---

最常用的度量

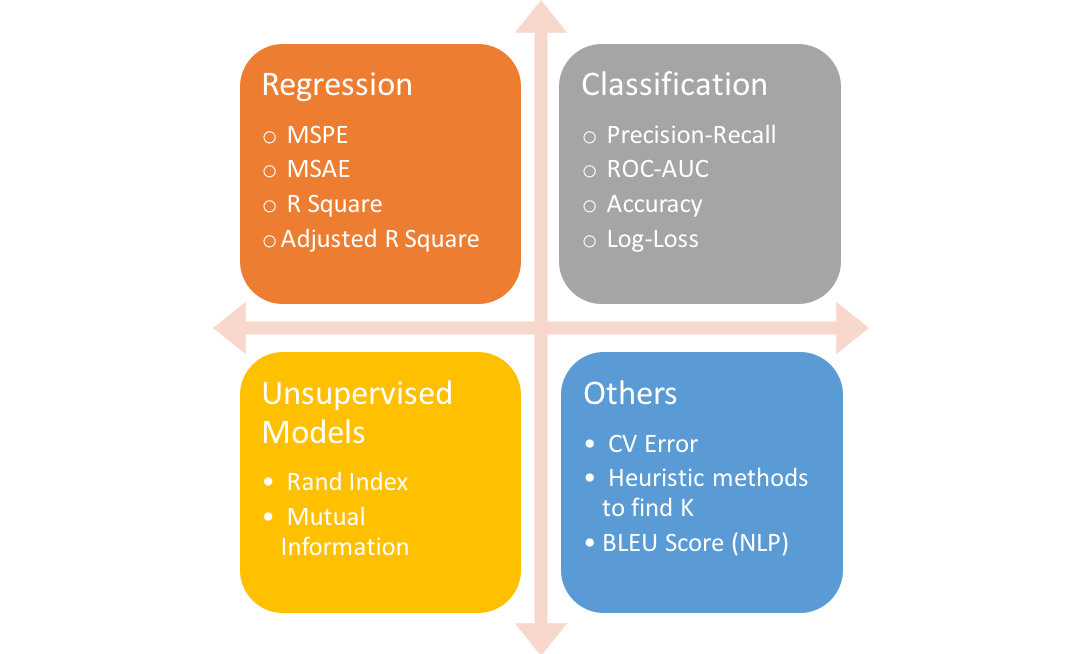
在第一篇博客中，我们将只讨论回归中的度量。

回归度量

大多数博客都关注分类指标，比如精确性、召回率、AUC等。为了改变这一点，我想探索各种指标，包括回归中使用的指标。MAE和RMSE是连续变量最常用的两种度量方法。

RMSE(均方根误差)

它表示预测值和观测值之间差异的样本标准差(称为残差)。从数学上讲，它是使用以下公式计算的：

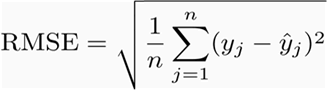
MAE

MAE是预测值和观测值之间绝对差的平均值。MAE是一个线性分数，这意味着所有的个体差异在平均值中的权重相等。例如，10和0之间的差是5和0之间的差的两倍。然而，RMSE的情况并非如此，我们将进一步详细讨论。从数学上讲，MAE是使用以下公式计算的：

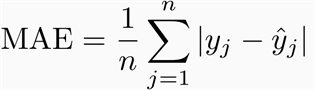
你应该选哪一个？为什么？

好吧，理解和解释MAE是很容易的，因为它直接取偏移量的平均值。与此对比，RMSE比MAE惩罚更高的差异。

让我们用两个例子来理解上面的陈述：

案例1：实际值=[2,4,6,8]，预测值=[4,6,8,10]

案例2：实际值=[2,4,6,8]，预测值=[4,6,8,12]

案例1的MAE=2，案例1的RMSE=2

病例2的MAE=2.5，病例2的RMSE=2.65

从上面的例子中，我们可以看到RMSE比MAE对最后一个值预测的惩罚更重。通常，RMSE的惩罚高于或等于MAE。它等于MAE的唯一情况是当所有的差异都等于或为零(在情况1中，所有观测值的实际和预测之间的差异都为2)。

然而，即使在更为复杂和偏向于更高的偏差之后，RMSE仍然是许多模型的默认度量，因为用RMSE定义的损失函数是光滑可微的，并且更容易执行数学运算。

虽然这听起来不太令人愉快，但这是一个非常重要的原因，使它非常受欢迎。我将试着用数学的方法解释上面的逻辑。

让我们在一个变量中建立一个简单的线性模型：y=mx+b

在这里，我们试图找到“m”和“b”，我们有数据(x，y)。

如果我们用RMSE定义损失函数(J)：那么我们可以很容易得到m和b的梯度(使用梯度下降的工作原理)

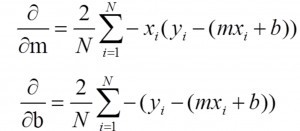
上述方程的求解比较简单，但是却不适用于MAE。

然而，如果你只想从解释的角度比较两个模型，那么我认为MAE是一个更好的选择。需要注意的是，RMSE和MAE的单位都与y值相同，因为RMSE的公式进行了开根操作。RMSE和MAE的范围是从0到无穷大。

注意：MAE和RMSE之间的一个重要区别是，最小化一组数字上的平方误差会得到平均值，最小化绝对误差会得到中值。这就是为什么MAE对异常值是健壮的，而RMSE不是。

R方(R^2)与调整R方

R方与调整R方通常用于解释目的，并解释所选自变量如何很好地解释因变量的可变性。

从数学上讲，R方由以下公式给出：

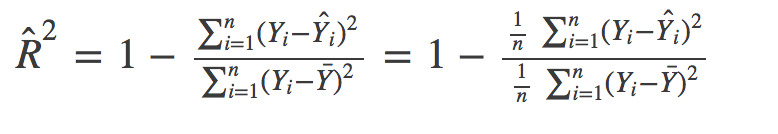
分子是MSE(残差平方的平均值)，分母是Y值的方差。MSE越高，R方越小，模型越差。

调整R方

与R方一样，调整R方还显示了曲线或直线的拟合程度，但会根据模型中项的变化进行调整。公式如下：

其中n是样本总数，k是变量数。调整R方始终小于或等于R方

为什么要选择调整R方而不是R方

常规的R方存在一些问题，可以通过调整R方来解决。调整R方将考虑模型中附加项所增加的边际改进。所以如果你加上有用的数据，它会增加，如果你加上不那么有用的变量，它会减少。

然而，R方会随着数据的增加而增加，但是模型并没有任何改进。用一个例子来理解这一点会更容易。

这里，情况1是一个简单的情况，我们有5个(x，y)的观测值。在案例2中，我们还有一个变量，它是变量1的两倍(与var 1完全相关)。在案例3中，我们在var2中产生了一个轻微的扰动，使得它不再与var1完全相关。

因此，如果我们为每一种情况拟合简单的普通最小二乘(OLS)模型，那么在逻辑上，我们就不会为情况2和情况3提供关于情况1的任何额外或有用的信息。因此，我们的度量值在这些模型上不应该增加。对于情况2和情况3，R方会增加或与之前相等。调整R方可以解决这个问题，在情况2和情况3调整R方会减少。让我们给这些变量(x，y)一些数字，看看Python中得到的结果。

注：模型1和模型2的预测值都是相同的，因此，R方也将是相同的，因为它只取决于预测值和实际值。

从上表中，我们可以看到，尽管我们没有在案例1和案例2中添加任何附加信息，但R方仍在增加，而调整R方显示出正确的趋势(对更多变量的模型2进行惩罚)

调整R方与RMSE的比较

对于上一个示例，我们将看到案例1和案例2的RMSE与R方类似。在这种情况下，调整后的R方比RMSE做得更好，RMSE的范围仅限于比较预测值和实际值。

此外，RMSE的绝对值实际上并不能说明模型有多糟糕。它只能用于两个模型之间的比较，而调整R方很容易做到这一点。例如，如果一个模型的调整R方为0.05，那么它肯定很差。

然而，如果你只关心预测的准确性，那么RMSE是最好的。它计算简单，易于微分，是大多数模型的默认度量。

常见的误解是：我经常在网上看到R的范围在0到1之间，这实际上不是真的。R方的最大值为1，但最小值可以为负无穷大。考虑这样一种情况，即模型预测所有观测值的高度负值，即使y的实际值为正值。在这种情况下，R方将小于0。这是极不可能的情况，但这种可能性仍然存在。

NLP中的一个度量

如果你对NLP感兴趣，这里有一个有趣的度量。

BLEU

它主要用于衡量机器翻译相对于人工翻译的质量。它使用一种改进的精度度量形式。

计算BLEU分数的步骤：

1. 将句子转换成单元、双元、三元和四元(unigrams, bigrams, trigrams, and 4-grams)

2. 对于大小为1到4的n-gram计算精度

3. 取所有这些精度值的加权平均值的指数

4. 乘以简短的惩罚(稍后解释)

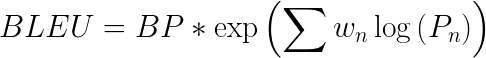
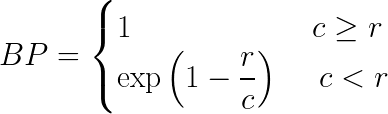
这里BP是简洁性惩罚，r和c是参考词和候选词的个数，w是权重，P是精度值

例子：

参考翻译：The cat is sitting on the mat

机器翻译1：On the mat is a cat

机器翻译2：There is cat sitting cat

让我们把以上两个译文计算BLEU分数进行比较。

我用的是nltk.translate.bleu

最终结果：BLEU(MT1)=0.454，BLEU(MT2)=0.59

为什么我们要加上简洁性惩罚？

简洁性惩罚惩罚候选短于他们的参考翻译。例如，如果候选是“The cat”，那么它对于unigram和bigram将具有高精度，因为这两个词在参考翻译中也是以相同的顺序出现。然而，长度太短，并没有真正反映出实际意义。

有了这个简短性惩罚，高分的候选译文现在必须在长度、单词和单词顺序方面与参考匹配。

原文链接：https://medium.com/usf-msds/choosing-the-right-metric-for-machine-learning-models-part-1-a99d7d7414e4

欢迎关注磐创AI博客站：
http://panchuang.net/

sklearn机器学习中文官方文档：
http://sklearn123.com/

欢迎关注磐创博客资源汇总站：
http://docs.panchuang.net/