题目描述:
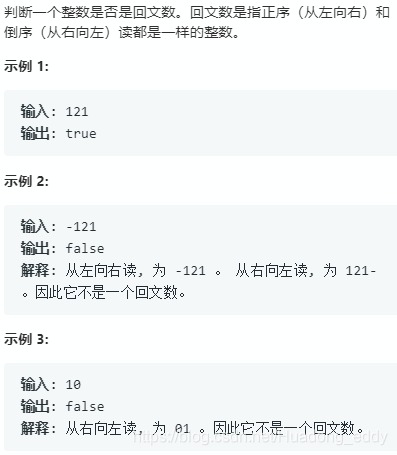
解法一(转换为字符串):
class Solution {
public:
bool isPalindrome(int x) {
string temp=to_string(x);
return isPalindrome(temp);
}
bool isPalindrome(string& temp){
int l=0,r=temp.size()-1;
while(l<r){
if(temp[l]!=temp[r])
return false;
l++;r--;
}
return true;
}
};解法二(数学解法):
通过取整和取余操作获取整数中对应的数字进行比较。
举个例子:1221 这个数字。
通过计算 1221 / 1000, 得首位1
通过计算 1221 % 10, 可得末位 1
进行比较
再将 22 取出来继续比较
class Solution {
public:
bool isPalindrome(int x) {
if(x<0) return false;
int div=1;
while(x/div>=10) div*=10;
while(x>0){
if(x/div!=x%10) return false;
x=(x%div)/10;
div/=100;
}
return true;
}
};解法三(数学法进阶):
直观上来看待回文数的话,就感觉像是将数字进行对折后看能否一一对应。
所以这个解法的操作就是 取出后半段数字进行翻转。
这里需要注意的一个点就是由于回文数的位数可奇可偶,所以当它的长度是偶数时,它对折过来应该是相等的;当它的长度是奇数时,那么它对折过来后,有一个的长度需要去掉一位数(除以 10 并取整)。
具体做法如下:
每次进行取余操作 ( %10),取出最低的数字:y = x % 10
将最低的数字加到取出数的末尾:revertNum = revertNum * 10 + y
每取一个最低位数字,x 都要自除以 10
判断 x 是不是小于 revertNum ,当它小于的时候,说明数字已经对半或者过半了
最后,判断奇偶数情况:如果是偶数的话,revertNum 和 x 相等;如果是奇数的话,最中间的数字就在revertNum 的最低位上,将它除以 10 以后应该和 x 相等。
class Solution {
public:
bool isPalindrome(int x) {
// 特殊情况:
// 如上所述,当 x < 0 时,x 不是回文数。
// 同样地,如果数字的最后一位是 0,为了使该数字为回文,
// 则其第一位数字也应该是 0
// 只有 0 满足这一属性
if(x<0||(x%10==0&&x!=0)) return false;
int temp=0;
while(x>temp){
temp=temp*10+x%10;
x/=10;
}
// 当数字长度为奇数时,我们可以通过 revertedNumber/10 去除处于中位的数字。
// 例如,当输入为 12321 时,在 while 循环的末尾我们可以得到 x = 12,revertedNumber = 123,
// 由于处于中位的数字不影响回文(它总是与自己相等),所以我们可以简单地将其去除。
return x==temp||x==temp/10;
}
};参考:https://leetcode-cn.com/problems/palindrome-number/solution/hui-wen-shu-by-leetcode/