$ color{#0066ff}{ 题目描述 }$
一年一度的“幻影阁夏日品酒大会”隆重开幕了。大会包含品尝和趣味挑战 两个环节,分别向优胜者颁发“首席品酒家”和“首席猎手”两个奖项,吸引了众多品酒师参加。
在大会的晚餐上,调酒师 Rainbow 调制了 n 杯鸡尾酒。这 n 杯鸡尾酒排成一行,其中第 n 杯酒 (1 ≤ i ≤ n) 被贴上了一个标签si,每个标签都是 26 个小写 英文字母之一。设 str(l, r)表示第 l 杯酒到第 r 杯酒的 r − l + 1 个标签顺次连接构成的字符串。若 str(p, po) = str(q, qo),其中 1 ≤ p ≤ po ≤ n, 1 ≤ q ≤ qo ≤ n, p ≠ q, po − p + 1 = qo − q + 1 = r ,则称第 p 杯酒与第 q 杯酒是“ r 相似” 的。当然两杯“ r 相似”(r > 1)的酒同时也是“ 1 相似”、“ 2 相似”、……、“ (r − 1) 相似”的。特别地,对于任意的 1 ≤ p , q ≤ n , p ≠ q ,第 p 杯酒和第 q 杯酒都 是“ 0 相似”的。
在品尝环节上,品酒师 Freda 轻松地评定了每一杯酒的美味度,凭借其专业的水准和经验成功夺取了“首席品酒家”的称号,其中第 i 杯酒 (1 ≤ i ≤ n) 的 美味度为 ai 。现在 Rainbow 公布了挑战环节的问题:本次大会调制的鸡尾酒有一个特点,如果把第 p 杯酒与第 q 杯酒调兑在一起,将得到一杯美味度为 ap*aq 的 酒。现在请各位品酒师分别对于 r = 0,1,2, ⋯ , n − 1 ,统计出有多少种方法可以 选出 2 杯“ r 相似”的酒,并回答选择 2 杯“ r 相似”的酒调兑可以得到的美味度的最大值。
(color{#0066ff}{输入格式})
第 1 行包含 1 个正整数 n ,表示鸡尾酒的杯数。
第 2 行包含一个长度为 n 的字符串 S,其中第 i 个字符表示第 i 杯酒的标签。
第 3 行包含 n 个整数,相邻整数之间用单个空格隔开,其中第 i 个整数表示第 i 杯酒的美味度 ai 。
(color{#0066ff}{输出格式})
包括 n 行。第 i 行输出 2 个整数,中间用单个空格隔开。第 1 个整 数表示选出两杯“ (i − 1) 相似”的酒的方案数,第 2 个整数表示选出两杯 “ (i − 1) 相似”的酒调兑可以得到的最大美味度。若不存在两杯“ (i − 1) 相似” 的酒,这两个数均为 0 。
(color{#0066ff}{输入样例})
10
ponoiiipoi
2 1 4 7 4 8 3 6 4 7
12
abaabaabaaba
1 -2 3 -4 5 -6 7 -8 9 -10 11 -12
(color{#0066ff}{输出样例})
45 56
10 56
3 32
0 0
0 0
0 0
0 0
0 0
0 0
0 0
66 120
34 120
15 55
12 40
9 27
7 16
5 7
3 -4
2 -4
1 -4
0 0
0 0
(color{#0066ff}{数据范围与提示})
用二元组 (p, q) 表示第 p 杯酒与第 q 杯酒。
0 相似:所有 45 对二元组都是 0 相似的,美味度最大的是 8 × 7 = 56 。
1 相似: (1,8) (2,4) (2,9) (4,9) (5,6) (5,7) (5,10) (6,7) (6,10) (7,10) ,最大的 8 × 7 = 56 。
2 相似: (1,8) (4,9) (5,6) ,最大的 4 × 8 = 32 。
没有 3,4,5, ⋯ ,9 相似的两杯酒,故均输出 0 。
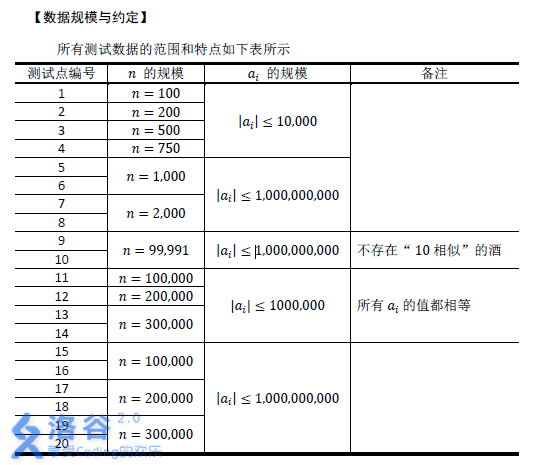
【时限1s,内存512M】
(color{#0066ff}{题解})
题中说:两杯“ r 相似”(r > 1)的酒同时也是“ 1 相似”、“ 2 相似”、……、“ (r − 1) 相似”的
显然这是个前缀的问题,那么我们考虑求恰好等于r的答案,然后统计一下前缀即可
两个相同子串??SAM的parent树点的不同孩子就行啊
注意!!!权值在左端点,因此我们要把序列翻转
答案一就是一个点孩子两两乘积之和, 答案二用子树的值更新,注意,有负数!!!,负负得正,所以还要维护最小值来更新答案,最后别忘取前缀信息,初始化的时候inf要极大!
#include<bits/stdc++.h>
#define LL long long
LL in() {
char ch; LL x = 0, f = 1;
while(!isdigit(ch = getchar()))(ch == '-') && (f = -f);
for(x = ch ^ 48; isdigit(ch = getchar()); x = (x << 1) + (x << 3) + (ch ^ 48));
return x * f;
}
const int maxn = 6e5 + 9;
const LL inf = 1e18 - 5;
LL ans1[maxn], ans2[maxn];
struct node {
node *ch[26], *fa;
int len, siz;
LL max, min;
node(int len = 0, int siz = 0, LL max = -inf, LL min = inf): fa(NULL), len(len), siz(siz), max(max), min(min) { memset(ch, 0, sizeof ch); }
}pool[maxn];
node *root, *tail, *lst, *id[maxn];
int t[maxn];
void init() {
tail = pool;
lst = root = new(tail++) node();
}
void extend(int c, LL val) {
node *o = new(tail++) node(lst->len + 1, 1, val, val), *v = lst;
for(; v && !v->ch[c]; v = v->fa) v->ch[c] = o;
if(!v) o->fa = root;
else if(v->len + 1 == v->ch[c]->len) o->fa = v->ch[c];
else {
node *n = new(tail++) node(v->len + 1), *d = v->ch[c];
std::copy(d->ch, d->ch + 26, n->ch);
n->fa = d->fa, d->fa = o->fa = n;
for(; v && v->ch[c] == d; v = v->fa) v->ch[c] = n;
}
lst = o;
}
void getans() {
int maxlen = 0, len = tail - pool;
for(node *i = pool; i != tail; i++) maxlen = std::max(maxlen, i->len), t[i->len]++;
for(int i = 1; i <= maxlen; i++) t[i] += t[i - 1];
for(node *i = pool; i != tail; i++) id[--t[i->len]] = i;
for(int i = len - 1; i; i--) {
node *o = id[i];
ans1[o->fa->len] += 1LL * o->fa->siz * o->siz;
o->fa->siz += o->siz;
if(o->fa->min != inf && o->min != inf) ans2[o->fa->len] = std::max(ans2[o->fa->len], o->fa->min * o->min);
if(o->fa->max != -inf && o->max != -inf) ans2[o->fa->len] = std::max(ans2[o->fa->len], o->fa->max * o->max);
o->fa->min = std::min(o->fa->min, o->min);
o->fa->max = std::max(o->fa->max, o->max);
}
}
char s[maxn];
LL val[maxn];
int main() {
int n = in();
init();
scanf("%s", s);
for(int i = 0; i < n; i++) val[i] = in();
std::reverse(s, s + n);
std::reverse(val, val + n);
for(int i = 0; i < n; i++) extend(s[i] - 'a', val[i]);
for(int i = 0; i < n; i++) ans2[i] = -inf;
getans();
for(int i = n - 2; i >= 0; i--) {
ans1[i] += ans1[i + 1];
ans2[i] = std::max(ans2[i], ans2[i + 1]);
}
for(int i = 0; i < n; i++) printf("%lld %lld
", ans1[i], ans2[i] == -inf? 0 : ans2[i]);
return 0;
}