(color{#0066ff}{ 题目描述 })
lxhgww的小名叫”小L“,这是因为他总是很喜欢L型的东西。小L家的客厅是一个R*C的矩形,现在他想用L型的地板来铺满整个客厅,客厅里有些位置有柱子,不能铺地板。现在小L想知道,用L型的地板铺满整个客厅有多少种不同的方案?需要注意的是,如下图所示,L型地板的两端长度可以任意变化,但不能长度为0。
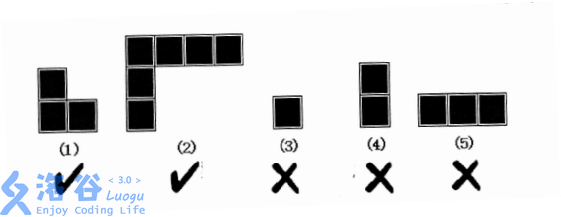
铺设完成后,客厅里面所有没有柱子的地方都必须铺上地板,但同一个地方不能被铺多次。
(color{#0066ff}{输入格式})
输入的第一行包含两个整数,R和C,表示客厅的大小。接着是R行,每行C个字符。'_'表示对应的位置是空的,必须铺地板;'*'表示对应的位置有柱子,不能铺地板。
(color{#0066ff}{输出格式})
输出包含q行,第i行为m[i]个整数,该行的第j(j=1,2...,,m[i])个数表示第i年被授权的聚居地h[j]的临时议事处管理的种族个数。
(color{#0066ff}{输入样例})
3 3
___
_*_
___
(color{#0066ff}{输出样例})
8
(color{#0066ff}{数据范围与提示})
测试点编号 数据范围
1,2 R*C<=25
3-5 R*C<=100并且(R=2或者C=2)
6-10 R*C<=100
(color{#0066ff}{ 题解 })
一道不错的插头DP
情况要考虑全面
考虑插头,0:无,1:未拐弯插头,2:已拐弯插头(题中要求必须是拐弯的砖)
套板子就行啦
再次声明,我TM就不写hash表,暴力卡常开(O2),980ms卡过去!!!
// luogu-judger-enable-o2
#include<bits/stdc++.h>
#define LL long long
LL in() {
char ch; LL x = 0, f = 1;
while(!isdigit(ch = getchar()))(ch == '-') && (f = -f);
for(x = ch ^ 48; isdigit(ch = getchar()); x = (x << 1) + (x << 3) + (ch ^ 48));
return x * f;
}
std::unordered_map<int, int> f[2];
int n, m, s, t;
bool mp[120][120];
char getch() {
char ch = getchar();
while(ch != '*' && ch != '_') ch = getchar();
return ch;
}
void init() {
n = in(), m = in();
static bool cp[120][120];
for(int i = 1; i <= n; i++)
for(int j = 1; j <= m; j++)
cp[i][j] = getch() == '_';
if(m > n) {
std::swap(n, m);
for(int i = 1; i <= n; i++)
for(int j = 1; j <= m; j++) {
mp[i][j] = cp[j][i];
if(mp[i][j]) s = i, t = j;
}
}
else {
for(int i = 1; i <= n; i++)
for(int j = 1; j <= m; j++) {
mp[i][j] = cp[i][j];
if(mp[i][j]) s = i, t = j;
}
}
}
const int mod = 20110520;
int pos(int v, int x) { return (v << (x << 1LL)); }
void ins(int &x, int y) { x %= mod, (x += y) %= mod; }
int work() {
int now = 0, nxt = 1;
int ans = 0;
f[now][0] = 1;
int U = (1 << ((m + 1) << 1)) - 1;
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= m; j++) {
f[nxt].clear();
for(auto &k:f[now]) {
int S = k.first, val = k.second;
int L = (S >> ((j - 1) << 1)) & 3, R = (S >> (j << 1)) & 3;
if(!mp[i][j]) {
if(!L && !R) ins(f[nxt][S], val);
continue;
}
if(!L && !R) {
//right 1
if(mp[i][j + 1]) ins(f[nxt][S ^ pos(1, j)], val);
//down 1
if(mp[i + 1][j]) ins(f[nxt][S ^ pos(1, j - 1)], val);
//middle double 2
if(mp[i][j + 1] && mp[i + 1][j]) ins(f[nxt][S ^ pos(2, j - 1) ^ pos(2, j)], val);
}
//要么直走还是1,要么拐弯变成2
else if(L == 0 && R == 1) {
if(mp[i + 1][j]) ins(f[nxt][S ^ pos(1, j - 1) ^ pos(1, j)], val);
if(mp[i][j + 1]) ins(f[nxt][S ^ pos(1, j) ^ pos(2, j)], val);
}
//要么直走还是2,要么停下变成0
else if(L == 0 && R == 2) {
if(mp[i + 1][j]) ins(f[nxt][S ^ pos(2, j - 1) ^ pos(2, j)], val);
ins(f[nxt][S ^ pos(2, j)], val);
}
//跟上面差不多
else if(L == 1 && R == 0) {
if(mp[i][j + 1]) ins(f[nxt][S ^ pos(1, j - 1) ^ pos(1, j)], val);
if(mp[i + 1][j]) ins(f[nxt][S ^ pos(1, j - 1) ^ pos(2, j - 1)], val);
}
else if(L == 2 && R == 0) {
if(mp[i][j + 1]) ins(f[nxt][S ^ pos(2, j - 1) ^ pos(2, j)], val);
ins(f[nxt][S ^ pos(2, j - 1)], val);
}
//必须拼上,没有其他情况
else if(L == 1 && R == 1) {
ins(f[nxt][S ^ pos(1, j - 1) ^ pos(1, j)], val);
}
//这些情况都是不成立的
else if(L == 1 && R == 2) {}
else if(L == 2 && R == 1) {}
else if(L == 2 && R == 2) {}
if(i == s && j == t) {
//1 1 // 0 2 // 2 0 第一个是接上,后两个是直接停下,都可以收集ans
if(L + R == 2) ins(ans, val);
}
}
std::swap(now, nxt);
}
f[nxt].clear();
for(auto &k:f[now]) ins(f[nxt][(k.first << 2) & U], k.second);
std::swap(nxt, now);
}
return ans;
}
int main() {
init();
printf("%d
", work() % mod);
return 0;
}