SBT
上一篇:平衡树学习笔记(4)-------替罪羊树
所谓SBT,就是Size Balanced Tree
它的速度很快,完全碾爆Treap,Splay等平衡树,而且代码简洁易懂
尤其是插入节点多的时候,比其它树快多了(不考虑毒瘤红黑树)
尤其是它的平衡操作maintain,均摊(O(1))!!!!
他maintain跟Splay差不多,都是依靠旋转来平衡
不过他可不想splay那样直接转到根,而是有条件的旋转
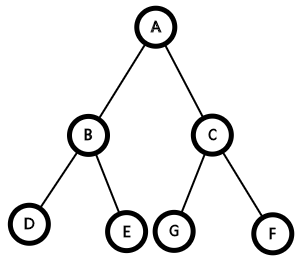
拿上图来说,SBT对于每个点,有两个平衡条件,假设说当前点是A,那么要满足以下两个条件,A才平衡
1、(siz(B)ge siz(G),siz(F))
2、(siz(C)ge siz(D),siz(E))
(color{#9900ff}{定义})
struct node {
node *ch[2];
int val, siz;
node(int val = 0, int siz = 0): val(val), siz(siz) { ch[0] = ch[1] = NULL; } //构造函数
void upd() { siz = ch[0]->siz + ch[1]->siz + 1; } //维护siz
int rk() { return ch[0]->siz + 1; } //获取当前排名
}*root, *null, pool[maxn], *tail, *st[maxn]; // 根,哨兵,内存池,当前指针,回收池
定义根Splay差不多,只是不用记录父亲
这里可以建立一个哨兵null,判断siz的时候比较好写
(color{#9900ff}{基本操作})
1、rotate
这个是旋转,跟Splay差不多
但是SBT是不用记录父亲的,所以要简单一点
这里有2个参数rotate(x,k)
意为把x向它的孩子k方向转
即为把x的另一个孩子!k转上来
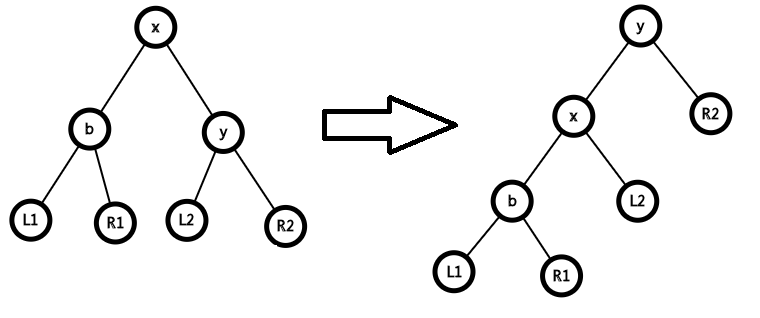
void rot(node *&x, int k) { //注意这里要取地址,maintain的时候也要取地址,目的是让x维护的是位置,而不是特定的点
node *w = x->ch[!k]; //w就是上图的L2,即旋转中特殊的那个点
x->ch[!k] = w->ch[k], w->ch[k] = x, w->siz = x->siz;
x->upd(), x = w; //让x仍然维护原来的位置
}
2、maintain
这是SBT维护平衡的操作函数
它基于1.rotate进行各种旋转
虽然看起来复杂度有点高
其实均摊可以达到(O(1))!(虽然我不会证)
维护平衡一定要考虑全面,一旦露了某个子树,可能就会被卡QWQ
首先,先声明一点,maintain只有插入才会用到
因为删除不会增加复杂度,其它操作,树的形态又没变
因此,用到maintain的唯有插入
插入怎么插呢?
我们采用的是递归插入(必须递归插入,因为沿途每个点siz一变大,就可能不平衡!)
沿途siz++
那么,很显然可以得到从它到根的一条链
由于沿途siz++,所以
途中的这些点都有可能需要平衡
maintain(x,k)代表平衡x,至于k,左右哪边重,k就是哪边
下面我们开始分情况讨论一下maintain操作
我们发现,俩条件是对称的!下面我们只讨论一个条件,另一个就是反过来而已
Case 1: siz(A) > siz(R)
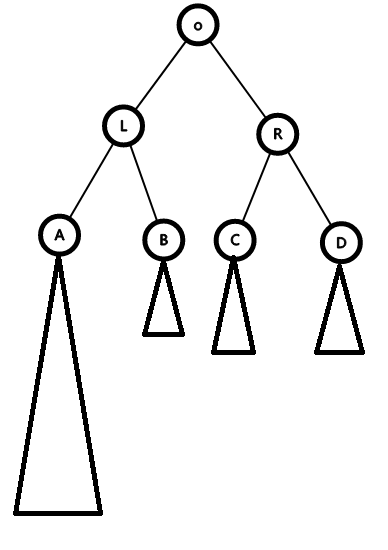
这时候我们把L转上来,就成了这样
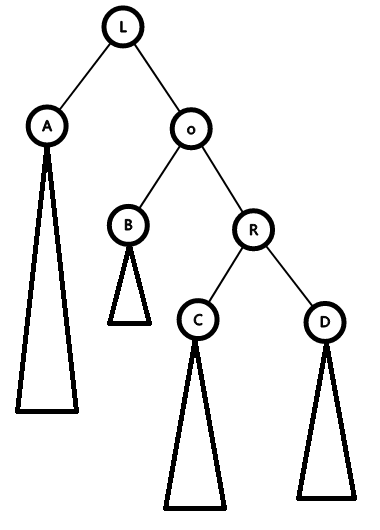
但是o可能还是不平衡,比如上图,右边偏重,所以我们要继续maintain
Case 2: siz(B) >siz(R)
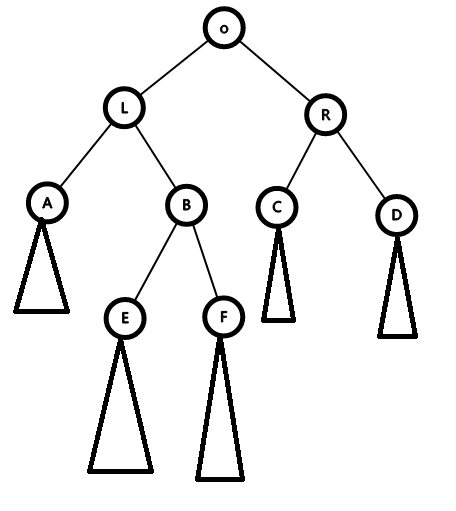
这时,我们把B直接转到o的位置上,即B左旋再右旋
然后,树就变成了这个样子
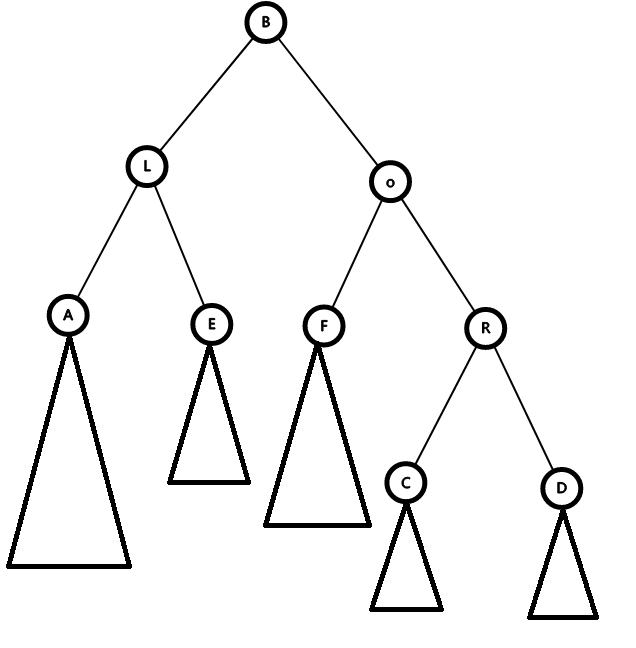
这时候会有好多地方不平衡qwq,但是可以发现,AEFR这些子树只是换了个位置,没有变,依然满足性质
因此我们调用两次maintain来平衡L和o
这个时候,除了B,其它所有点的子树都OK了,就剩下B了,它可能不满足1或2,所以再maintain(B)一下
代码实现的时候,可以记录一下哪边重,然后就可以写到一起,很简洁,好记
void maintain(node *&o, int k) { //平衡o,哪边重,k就是哪边
if(o->ch[k]->ch[k]->siz > o->ch[!k]->siz) rot(o, !k); //情况1,
else if(o->ch[k]->ch[!k]->siz > o->ch[!k]->siz) rot(o->ch[k], k), rot(o, !k); //情况2
else return;
maintain(o->ch[0], 0), maintain(o->ch[1], 1), maintain(o, 0), maintain(o, 1); //统一平衡,即使有些情况不涉及,反正递归下去也是直接return
}
(ecolor{#9900ff}{其它操作})
1、插入
关于插入,上面提了几句
总的来说就是从根出发,往孩子跳
这是一个递归的过程,必须递归,因为沿途回溯的时候要maintain,当然手动模拟递归也不拦你
void ins(node *&o, int val) {
if(o == null) return (void)(o = newnode(val)); //到空节点,直接开新节点就行
o->siz++; //沿途siz++
if(val <= o->val) ins(o->ch[0], val); //找到插入位置
else ins(o->ch[1], val);
maintain(o, val > o->val); //每个点的子树进行平衡,在哪边插的,哪边可能就会变重,所以要平衡那一边
}
2、删除
因为它并没有Splay那样直接转到根这样的条件
它的旋转只是基于siz来的
所以,我们需要一些特别的方式
首先我们找到要删除的那个点,如果发现那个点并不是左右儿子都有,那就把那个儿子接上来就行了
否则,它一定存在左右儿子,也就是说它有后继,我们可以直接暴力找到它的后继,然后点权赋过来,改成在右边删除它的后继
见代码
void del(node *&o, int val) {
//只要没找到,就递归删
if(o->val != val) return (void)(del(o->ch[val > o->val], val), o->upd());
//删除同理,沿途siz--
o->siz--;
//定义一个临时变量p为当前节点
node *p = o;
//如果x有一个孩子是空的,那么就简单了
//把他不空的孩子接上来代替他的位置
//显然不会影响平衡树的性质
//这时只需把p删了即可
if(o->ch[0] == null) o = o->ch[1], st[++top] = p;
else if(o->ch[1] == null) o = o->ch[0], st[++top] = p;
else {
//这就是没有空孩子的情况
p = o->ch[1];
while(p->ch[0] != null) p = p->ch[0];
//让p为o的后继(暴力找)
//除了siz之外,二者全部交换
//虽然o的值变成了p的
//但是p的值没有改变!!!
//因此,我们相当于已经用p代替了o
//而且,因为p是o的后继,所以接上一定是满足平衡树性质的!
//所以,我们的目标就只有一个了,那就是删掉p
//而p作为后继,一定在o的右子树内
//而且通过刚刚找后继的方式来看,它的左儿子一定是空的
//所以当前位置的递归最多只会进入一次
//这样也保证了复杂度!
o->val = p->val, del(o->ch[1], p->val);
}
}
上面一定要理解透彻
3、查询数x的排名
剩下的就差不多了qwq
int rnk(int val) {
node *o = root; int rank = 0;
while(o != null) {
if(o->val < val) rank += o->rk(), o = o->ch[1];
else o = o->ch[0];
}
return rank + 1;
}
4、查询第k大的数
int kth(int k) {
node *o = root;
while(o->rk() != k) {
if(k > o->rk()) k -= o->rk(), o = o->ch[1];
else o = o->ch[0];
}
return o->val;
}
5,6、前驱,后继
跟Splay的一毛一样qwq
毕竟都是平衡树,多少有点通性
int pre(int val) {
node *o = root, *lst = null;
while(o != null) {
if(o->val < val) lst = o, o = o->ch[1];
else o = o->ch[0];
}
return lst->val;
}
int nxt(int val) {
node *o = root, *lst = null;
while(o != null) {
if(o->val > val) lst = o, o = o->ch[0];
else o = o->ch[1];
}
return lst->val;
}
最后,放下完整代码
#include<bits/stdc++.h>
#define LL long long
LL in() {
char ch; LL x = 0, f = 1;
while(!isdigit(ch = getchar()))(ch == '-') && (f = -f);
for(x = ch ^ 48; isdigit(ch = getchar()); x = (x << 1) + (x << 3) + (ch ^ 48));
return x * f;
}
const int maxn = 1e5 + 10;
struct SBT {
protected:
struct node {
node *ch[2];
int val, siz;
node(int val = 0, int siz = 0): val(val), siz(siz) { ch[0] = ch[1] = NULL; }
void upd() { siz = ch[0]->siz + ch[1]->siz + 1; }
int rk() { return ch[0]->siz + 1; }
}*root, *null, pool[maxn], *tail, *st[maxn];
int top;
node *newnode(int val) {
node *o = new(top? st[top--] : tail++) node(val, 1);
return o->ch[0] = o->ch[1] = null, o;
}
void rot(node *&x, int k) {
node *w = x->ch[!k];
x->ch[!k] = w->ch[k], w->ch[k] = x, w->siz = x->siz;
x->upd(), x = w;
}
void maintain(node *&o, int k) {
if(o->ch[k]->ch[k]->siz > o->ch[!k]->siz) rot(o, !k);
else if(o->ch[k]->ch[!k]->siz > o->ch[!k]->siz) rot(o->ch[k], k), rot(o, !k);
else return;
maintain(o->ch[0], 0), maintain(o->ch[1], 1), maintain(o, 0), maintain(o, 1);
}
void ins(node *&o, int val) {
if(o == null) return (void)(o = newnode(val));
o->siz++;
if(val <= o->val) ins(o->ch[0], val);
else ins(o->ch[1], val);
maintain(o, val > o->val);
}
void del(node *&o, int val) {
if(o->val != val) return (void)(del(o->ch[val > o->val], val), o->upd());
o->siz--;
node *p = o;
if(o->ch[0] == null) o = o->ch[1], st[++top] = p;
else if(o->ch[1] == null) o = o->ch[0], st[++top] = p;
else {
p = o->ch[1];
while(p->ch[0] != null) p = p->ch[0];
o->val = p->val, del(o->ch[1], p->val);
}
}
public:
SBT() {
tail = pool; top = 0;
root = null = new node();
null->ch[0] = null->ch[1] = null;
}
void ins(int val) { ins(root, val); }
void del(int val) { del(root, val); }
int rnk(int val) {
node *o = root; int rank = 0;
while(o != null) {
if(o->val < val) rank += o->rk(), o = o->ch[1];
else o = o->ch[0];
}
return rank + 1;
}
int kth(int k) {
node *o = root;
while(o->rk() != k) {
if(k > o->rk()) k -= o->rk(), o = o->ch[1];
else o = o->ch[0];
}
return o->val;
}
int pre(int val) {
node *o = root, *lst = null;
while(o != null) {
if(o->val < val) lst = o, o = o->ch[1];
else o = o->ch[0];
}
return lst->val;
}
int nxt(int val) {
node *o = root, *lst = null;
while(o != null) {
if(o->val > val) lst = o, o = o->ch[0];
else o = o->ch[1];
}
return lst->val;
}
}s;
int main() {
for(int T = in(); T --> 0;) {
int p = in();
if(p == 1) s.ins(in());
if(p == 2) s.del(in());
if(p == 3) printf("%d
", s.rnk(in()));
if(p == 4) printf("%d
", s.kth(in()));
if(p == 5) printf("%d
", s.pre(in()));
if(p == 6) printf("%d
", s.nxt(in()));
}
return 0;
}
下一篇:平衡树学习笔记(6)-------RBT





