def merge(a, b):
x = []
while len(a) > 0 and len(b) > 0:
if a[0] < b[0]:
x.append(a.pop(0))
else:
x.append(b.pop(0))
while len(a) > 0:
x.append(a.pop(0))
while len(b) > 0:
x.append(b.pop(0))
return x
def halve(x):
half = len(x) / 2
return x[:half], x[half:]
def recursiveMergeSort(x):
if len(x) == 1:
return x
a, b = halve(x)
a = recursiveMergeSort(a)
b = recursiveMergeSort(b)
return merge(a, b)
def iterativeMergeSort(x):
queue = [[i] for i in x]
while len( queue ) > 1:
a, b = queue.pop(0), queue.pop(0)
queue.append(merge(a, b))
return queue[0]
x = [40, 82, 97, 47, 7]
assert recursiveMergeSort(x) == [7, 40, 47, 82, 97]
assert iterativeMergeSort(x) == [7, 40, 47, 82, 97]
python 归并排序
归并排序要点:
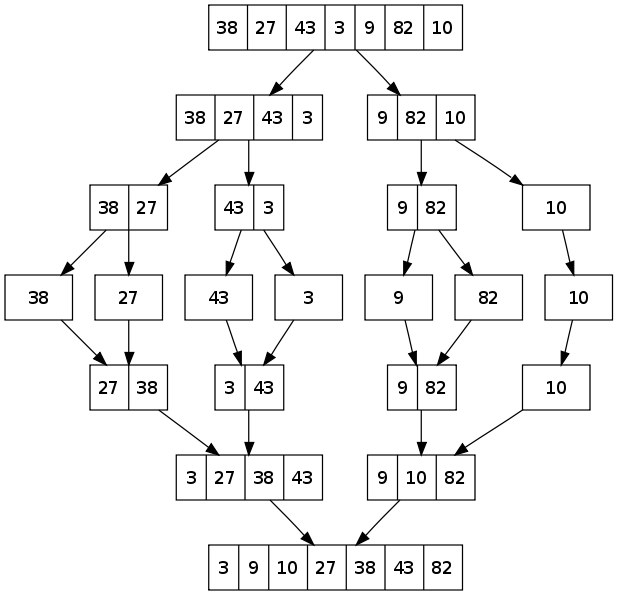
1. 自顶向下分拆,之后又合并,当然符合递归的一般形式,先递后归嘛
2. 融合merge算法的合理性:a与b的头指针,若a的小于b的,则a指针数据小于b的全部,同时它自然小于a自己的剩余数据,故其可以被添加为当前最小值
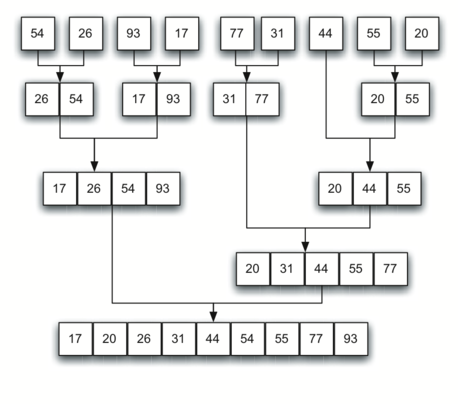
3. 迭代算法产生合并对象时,就是分拆成多个小的有序数组,新生成的照样可以加入,执行合并;任意两个有序数组都可以进行归并得到有序的数组,所以归并的顺序无所谓,并不需要遵循上图的层次顺序。
http://connor-johnson.com/2016/05/17/sorting-algorithms-in-python/

