QR分解:

有很多方法可以进行QR迭代,本文使用的是Schmidt正交化方法
具体证明请参考链接 https://wenku.baidu.com/view/c2e34678168884868762d6f9.html
迭代格式
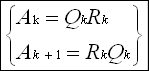
实际在进行QR分解之前一般将矩阵化为上hessnberg矩阵(奈何这个过程比较难以理解,本人智商不够,就不做这一步了哈哈哈)
迭代终止条件
看了很多文章都是设置一个迭代次数,感觉有些不是很合理,本来想采用A(k+1)-A(k)的对角线元素的二范数来作为误差的,但是我有没有一些严格的证明,所以本文也采用比较大众化的思路,设置迭代次数。
Python实现
1 M = [[2, 4, 2], [-1, 0, -4], [2, 2, 1]] 2 3 import copy 4 import math 5 6 7 class QR(object): 8 9 def __init__(self, data): 10 self.M = data 11 self.degree = len(data) 12 13 def get_row(self, index): 14 res = [] 15 for i in range(self.degree): 16 res.append(self.M[i][index]) 17 return res 18 19 def get_col(self, index): 20 res = [] 21 for i in range(self.degree): 22 res.append(self.M[i][index]) 23 return res 24 25 @staticmethod 26 def dot(m1, m2): 27 res = 0 28 for i in range(len(m1)): 29 res += m1[i] * m2[i] 30 return res 31 32 @staticmethod 33 def list_multi(k, lt): 34 res = [] 35 for i in range(len(lt)): 36 res.append(k * lt[i]) 37 return res 38 39 @staticmethod 40 def one_item(x, yArr): 41 res = [0 for i in range(len(x))] 42 temp_y_arr = [] 43 44 n = len(yArr) 45 if n == 0: 46 res = x 47 else: 48 for item in yArr: 49 k = QR.dot(x, item) / QR.dot(item, item) 50 temp_y_arr.append(QR.list_multi(-k, item)) 51 temp_y_arr.append(x) 52 53 for item in temp_y_arr: 54 for i in range(len(item)): 55 res[i] += item[i] 56 return res 57 58 @staticmethod 59 def normal(matrix): 60 yArr = [] 61 yArr.append(matrix[0]) 62 63 for i in range(1, len(matrix)): 64 yArr.append(QR.one_item(matrix[i], yArr)) 65 return yArr 66 67 @staticmethod 68 def normalized(lt): 69 res = [] 70 sm = 0 71 for item in lt: 72 sm += math.pow(item, 2) 73 sm = math.sqrt(sm) 74 for item in lt: 75 res.append(item / sm) 76 return res 77 78 @staticmethod 79 def matrix_T(matrix): 80 mat = copy.deepcopy(matrix) 81 m = len(mat[0]) 82 n = len(mat) 83 for i in range(m): 84 for j in range(n): 85 if i < j: 86 temp = mat[i][j] 87 mat[i][j] = mat[j][i] 88 mat[j][i] = temp 89 return mat 90 91 @staticmethod 92 def matrix_multi(mat1, mat2): 93 res = [] 94 rows = len(mat1[0]) 95 cols = len(mat1) 96 for i in range(rows): 97 temp = [0 for i in range(cols)] 98 res.append(temp) 99 100 for i in range(rows): 101 for j in range(cols): 102 sm = 0 103 for k in range(cols): 104 sm += (mat1[k][i] * mat2[j][k]) 105 res[j][i] = sm 106 return res 107 108 def execute(self): 109 xArr = [] 110 for i in range(self.degree): 111 xArr.append(self.get_col(i)) 112 yArr = QR.normal(xArr) 113 self.Q = [] 114 for item in yArr: 115 self.Q.append(QR.normalized(item)) 116 117 self.R = QR.matrix_multi(QR.matrix_T(self.Q), xArr) 118 return (self.Q, self.R) 119 120 121 # A = [ 122 # [1, 0, -1, 2, 1], 123 # [3, 2, -3, 5, -3], 124 # [2, 2, 1, 4, -2], 125 # [0, 4, 3, 3, 1], 126 # [1, 0, 8, -11, 4] 127 # ] 128 # A = [ 129 # [1, 2, 2], 130 # [2, 1, 2], 131 # [2, 2, 1] 132 # ] 133 A = [ 134 [3, 2, 4], 135 [2, 0, 2], 136 [4, 2, 3] 137 ] 138 139 temp = copy.deepcopy(A) 140 val = [] # 特征值 141 times = 20 # 迭代次数 142 for i in range(times): 143 qr = QR(temp) 144 (q, r) = qr.execute() 145 temp = QR.matrix_multi(r, q) 146 temp = QR.matrix_T(temp) 147 148 for i in range(len(temp)): 149 for j in range(len(temp[0])): 150 if i == j: 151 val.append(temp[i][j]) 152 # 特征值 153 print(val)
结果展示

总结
使用QR分解迭代求特征值,收敛的比较快,也可以求出所有的特征值,但是如果要求特征向量的话,还是需要求解线性方程组(感觉很麻烦)