2018秋招面试记录

作业帮笔试

leetcode 53 Maximum Subarray

Given an integer array nums, find the contiguous subarray (containing at least one number) which has the largest sum and return its sum.

Example:

Input: [-2,1,-3,4,-1,2,1,-5,4],
Output: 6
Explanation: [4,-1,2,1] has the largest sum = 6.

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        if (nums.empty()) {
            return -1;
        }
        int n = nums.size();
        int max_val = nums[0];
        int cur_max = 0;
        for (int i = 0; i < n; i++) {
            // 这样一来每次还会比较每个值的大小, 如果数组所有值为负数的话
            cur_max += nums[i]; 
            max_val = max(max_val, cur_max);
            cur_max = max(cur_max, 0);  // 很优秀
        }
        return max_val;
    }
};

爱奇艺面试

布丰投针问题

布丰投针问题



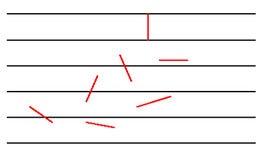
18世纪，布丰提出以下问题：设我们有一个以平行且等距木纹铺成的地板（如图），现在随意抛一支长度比木纹之间距离小的针，求针和其中一条木纹相交的概率。并以此概率，布丰提出的一种计算圆周率的方法——随机投针法。这就是布丰投针问题.

由于向桌面投针是随机的，所以用二维随机变量（X,Y）来确定它在桌上的具体位置。设 X 表示针的中点到平行线的的距离，Y 表示针与平行线的夹角，那么 X 在 ((0, frac{a}{2})) 服从均匀分布，Y 在 ((0, frac{pi}{2})) 服从均匀分布，X, Y 相互独立，由此可以写出 (X，Y) 的概率密度函数

[f(x, y) = egin{cases} frac{4}{pi a} quad 0 < x < frac{a}{2}, 0<y<frac{pi}{2} \ 0 quadquad others end{cases} ]

因此所求概率

[egin{align*} Pleft {X < frac{l}{2}sinY ight} &= intint_{X<frac{l}{2}sinY}quad f(x,y)space dxdy \ &= frac{4}{pi a}intint_{x<frac{l}{2}siny}space 1cdot dxdy \ &= frac{4}{pi a}int_0^{frac{pi}{2}}1cdot dy space int_0^{frac{l}{2}siny} 1cdot dx \ &= frac{4}{pi a}int_0^{frac{pi}{2}}frac{l}{2}sinycdot dy \ &= frac{4}{pi a}(-frac{l}{2}cosy|_{0}^{frac{pi}{2}}) \ &= frac{4}{pi a}frac{l}{2} \ &= frac{2l}{pi a} \ end{align*} ]

求概率分布

设 X ~ U(0, 1), 在 X=x(0<x<1)的条件下, Y在(0, x)内服从均匀分布, 求:

(I) (X, Y) ~ f(x, y)
(II) P(X+Y>1)

(I) 解答


[f_X(x)=egin{cases} 1 quad 0<x<1 \ 0 quad others end{cases} ]

[f_{Y|X}(y|x)=egin{cases} frac{1}{x} quad 0<y<x<1 \ 0 quad others end{cases} ]

[egin{align*} f(x, y) &= f_{Y|X}(y|x) space f_X(x) \ &=egin{cases} frac{1}{x} quad 0<y<x<1 \ 0 quad others end{cases} end{align*} ]

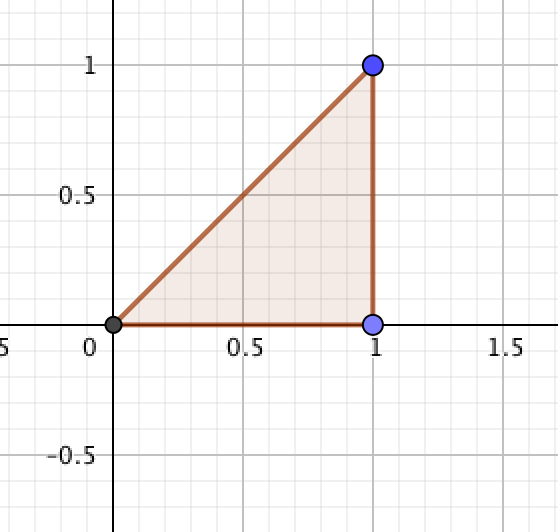
(II) 解答



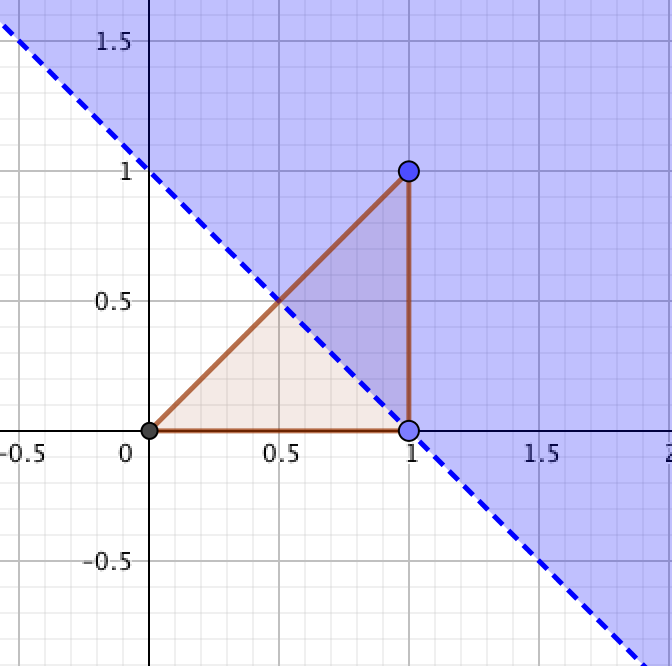
由上图可知, 先积 y(在 y 轴做积分) 简单, 如果先积 x, 分为 [0, 0.5])和[0.5, 1] 这两段.
根据积分口诀, 后积先定限, 限内画条线; 先交写下限, 后交写上限, 可得如下计算

[egin{align*} P(X+Y>1) & = intint_{X+Y>1} f(x, y)space dxdy \ &= int^1_{frac{1}{2}} frac{1}{x}cdot dxint^x_{1-x} 1cdot dy \ &= int^1_{frac{1}{2}} frac{1}{x} cdot (2x-1) dx \ &= 1 - ln2 end{align*} ]

Kmeans 聚类实现



更加全面的解法见 KMeans C++实现

更加好的判断聚类是不是结束的条件判断是设置一个判断聚类中心是否移动的阀值cosnt float DIST_NRAR = 0.001, 也就是说当两次聚类中心的差值小于此值时，聚类则停止。

下面是一个简单的实现, 很好的体现了算法的逻辑思路

#include<iostream>
#include<cmath>
#include<vector>
using namespace std;


// 点使用 vector<double> 来表示
struct Cluster {
    vector<double> centroid;
    vector<int> sample_indexes;
};

double cal_distance(vector<double> point1, vector<double> point2) {
    int dim = point1.size();
    double val = 0.0;
    for (int i = 0; i < dim; i++) {
        val += pow((point1[i] - point2[i]), 2);
    }
    return sqrt(val);
}
vector<Cluster> k_means(vector<vector<double> > dataset, int num_centroid, int max_epoches) {
    const int num_sample = dataset.size();
    const int dim = dataset[0].size();

    // 1. 初始化聚类中心
    vector<Cluster> clusters(num_centroid);
    for (int i = 0; i < num_centroid; i++) {
        int c = rand() % num_sample;
        clusters[i].centroid = dataset[c];
    }

    // 2. 多次迭代直至收敛
    for (int it = 0; it < max_epoches; it++) {
        // 每一次重新计算样本点所属类别之前，清空原来样本点信息
        for (int i = 0; i < num_centroid; i++) {
            clusters[i].sample_indexes.clear();
        }
        // 求出每个样本点距应该属于哪一个聚类
        for (int sample_index = 0; sample_index < num_sample; sample_index++) {
            // 开始时, 每个样本都初始化属于第0个聚类
            int true_centroid_index = 0;
            double min_distance = LONG_MAX;
            for (int centroid_index = 0; centroid_index < num_centroid; centroid_index++) {
                double distance = cal_distance(dataset[sample_index], clusters[centroid_index].centroid);
                if (distance < min_distance) {
                    min_distance = distance;
                    true_centroid_index = centroid_index;
                }
            }
            clusters[true_centroid_index].sample_indexes.push_back(sample_index);
        }

        // 3. 更新聚类中心
        for (int i = 0; i < num_centroid; i++) {
            vector<double> point(dim, 0.0);
            for (int j = 0; j < clusters[i].sample_indexes.size(); j++) {
                int sample = clusters[i].sample_indexes[j];
                for (int d = 0; d < dim; d++) {
                    point[d] += dataset[sample][d];
                    if (j == clusters[i].sample_indexes.size() - 1)
                        clusters[i].centroid[d] = point[d] / clusters[i].sample_indexes.size();
                }
            }
        }
    }
    return clusters;
}

int main()
{
    vector<vector<double> > trainX(9,vector<double>(1,0));
    // 对 9 个数据 {1 2 3 11 12 13 21 22 23} 聚类
    double data = 1.0;
    for (int i = 0; i < 9; i++) {
        trainX[i][0] = data;
        if ((i+1) % 3 == 0) data += 8;
        else data++;
    }

    // k-means聚类
    vector<Cluster> clusters_out = k_means(trainX, 3, 100);

    // 输出分类结果
    for (int i = 0; i < clusters_out.size(); i++) {
        cout << "Cluster " << i << " :" << endl;
        /*子类中心*/
        cout << "	" << "Centroid: " << "
		[ ";
        for (int j = 0; j < clusters_out[i].centroid.size(); j++) {
            cout << clusters_out[i].centroid[j] << " ";
        }
        cout << "]" << endl;

        /*子类样本点*/
        cout << "	" << "Samples:
";
        for (int k = 0; k < clusters_out[i].sample_indexes.size(); k++) {
            int c = clusters_out[i].sample_indexes[k];
            cout << "		[ ";
            for (int m = 0; m < trainX[0].size(); m++) {
                cout << trainX[c][m] << " ";
            }
            cout << "]
";
        }
    }
    return 0;
}

Momenta 电话面试记录

概率题

A, B 独立, 在 [0, 1] 均匀分布, C = max(A, B), 求 C 的数学期望.

[F_A(a) = P(A le a) = egin{cases} 0, quad a < 0 \ a, quad a in[0, 1] \ 1, quad a > 1 end {cases} ]

[F_B(b) = P(B le b) = egin{cases} 0, quad b < 0 \ b, quad b in[0, 1] \ 1, quad b > 1 end {cases} ]

[egin{align} F_C(c) &= P(C le c) = P(max(A, B) le c) \ &= P(A le c, B le c) = P(A le c) cdot P(B le c) \ &= egin{cases} 0, quad c < 0 \ c^2, quad cin [0, 1] \ 1, quad c > 1 end {cases} end{align} ]

[f(c) = (F_C)prime(c) = egin{cases} 2c, quad c in[0, 1] \ 0, quad others \ end {cases} ]

[E(c) = int_{0}^{1}c cdot 2c space dc = frac{2}{3} c^3|_{0}^{1} = frac{2}{3} ]

编程题

给定一个环状数组(长度未知，环状的意思是数组里第一个数和最后一个数相邻)，中间包含的数字全是正整数，取出其中的一些数字，但不能取出任何连续两个位置的数字。求取出的数字的和的最大值。

示例:［2, 3, 2, 1］返回4，[2, 2, 3,1] 返回5

// 由于第一个和最后一个绝不可能同时都被选择，所以搜索范围分两种情况
// 1.  0 ~ n-2
// 2.  1 ~ n-1

class Solution {
public:
    int rob(vector<int>& nums) {
        int size = int(nums.size());
        if (size == 0) return 0;
        if (size == 1) return nums[0];
        
        return max(rob(nums, 0, size-1), rob(nums, 1, size));
    }
    
    int rob(vector<int>& nums, int start, int end) {
        
        int two_before_cur = 0;
        int one_before_cur = 0;
        int cur_max = 0;
        
        for (int i = start; i < end; ++i) {
            cur_max = max(nums[i]+two_before_cur, one_before_cur);
            two_before_cur = one_before_cur;
            one_before_cur = cur_max;
        }
        
        return cur_max;   
    }
};

深度学习网络基础

Q: 如果很足够大的数据集, 使用 Knowledge Distillation 这种方法大网络训练小网络效果如何?

A: 效果很好, 由于模型越大容量和表达能力越强, 并且数据量足够大, 那么大模型的效果会很好(不会过拟合), 而小模型的容量和表达能力有限, 即使数据再多, 性能有瓶颈.

Q: 计算神经网络的计算量, 如果输入 Feature Map 为 (N, C, H, W), 卷积核为 (3, 3), stride 1, padding=1, channel=C, 求该层计算量?

A: 输出层的 Feature Map 为 (N, C, H, W), 其中每一个所需要的计算量为一个卷积核的一次卷积的计算量为 (3 imes3 imes C), 故该层计算量为 ((B imes H imes W imes C) imes (3^2 imes C)) (最好提一下, 有了 BN, 卷积的 bias 都不设置)

通用计算:

输入 Feature Map 大小: (N imes C_{in} imes H_{in} imes W_{in}),
输出 Feature Map 大小: (N imes C_{out} imes H_{out} imes W_{out})，
输出 Feature Map 每个点需要计算量: (C_{in} imes H_k imes W_k)
该层计算量: 因此一共需要 ((N imes C_{out} imes H_{out} imes W_{out})) x ((C_{in} imes H_k imes W_k)) 次 mulit_add
其中: (W_{out} = leftlfloor frac{W_{in} + 2 imes padding - W_k}{stride} ight floor + 1)

Q: 感受野计算, 4层网络, 第一层 (3, 3, stride=1), 第二层 max-pooling, (2, 2, stride=2), 第3层 (3, 3, stride=2), 第4层 (3, 3, stride=2), 求感受野.

A: 计算表达式 (kernel_size - stride) + size * stride

第4层卷积输出 Feature Map 上的 1 个点在 第三层输出 Feature Map 的感受野是 3;
第3层卷积输出 Feature Map 上的 3 个点在 第二层输出 Feature Map 的感受野是 3 + 2 x (3-1) = 7;
第2层卷积输出 Feature Map 上的 7 个点在 第一层输出 Feature Map 的感受野是 7 x 2 = 14
第1层卷积输出 Feature Map 上的 14 个点在输入图片上的感受野是 3 + 1x(14-1) = 16;

Q: 使用sigmoid 激活函数, 为何反向传播过程中, 梯度会消失?

[egin{align*} f space prime = y(1-y) \ end{align*} ]

在接近0, 1时, 函数梯度很小, 且当 (y = frac{1}{2}) 时取得最大值, 为 (frac{1}{4}), 即最大值 (frac{1}{4}), 故反向传播过程出现梯度弥散

一些开放问题 ?

Q. 做路口的车辆检测的话, 光流算法和目标检测算法的优缺点
A. 光流能更加准确的提取车辆的较为准确轮廓信息和运动信息, 不过只能检测运动的车辆, 而且车辆太多了, 效果不好, 车辆的阴影也会对检测车辆定位准确造成影响

Q. 如果路口有密集的车辆, 朝着同一方向前进, 有什么思路去提取车辆数量呢?
A: 这个使用光流解决有点困难, 由于运动方向相同, 我没有想到在光流算法上怎么去处理问题, 对于光流提取的车辆轮廓信息, 可以使用边缘检测算法提取一些边缘或者角点什么的?(乱回答~)

百度面试

1. 自我介绍, 说明自己的经历(家乡, 教育经历, 研究方向) 让面试官了解下你
2. 深度学习和传统机器学习的区别? 为何表格数据不适用 CNN?
3. 深度学习有哪些优化算法
4. 简单说下 CNN 的原理
5. 逻辑回归有为何使用 (e^{-wx}) ?
6. 有哪些分类算法 ?

和面试官方向不匹配, 尬聊了很久

猎豹移动

1. 建立大顶堆
2. 循环数组找一个数
3. 一个电脑, 2个 cpu, n 个任务, 所需时间 t, t 为正整数, 求完成全部任务的所需最小时间

1.建立大顶堆

// 这里操作的是大顶堆

// keep_heap 维持堆的性质, 时间复杂度 O(lgn)
// 1. 输入数组 nums 和下标 parent，假设左右孩子节点 left 和 right 的二叉树都是最大堆
// 2. nums[parent] 可能小于其孩子，这时违反了最大堆的性质
// 3. keep_heap 的作用就是让 A[parent] 在最大堆里逐级下降，
//    最后使得每一个子堆都满足最大堆的性质

void keep_heap(vector<int> &nums, int parent){
    int left = (parent+1)*2-1;
    int right = left + 1;
    int largest = parent;
    
    // 注意这里比较的是 nums[largest], 为了找到 parent, left, right 中的最大值
    if (left < nums.size() && nums[left] > nums[largest]) largest = left;
    if (right < nums.size() && nums[right] > nums[largest]) largest = right;

    if (largest != parent) {
        swap(nums[largest], nums[parent]);
        keep_heap(nums, largest);
    }
}

// 时间复杂度为线性时间复杂度 O(n)
// 证明: 当用数组表示存储 n 个元素的堆时, 叶节点的下标分别是 floor(n/2)+1, floor(n/2)+2, ..., n
// 我们知道，堆是一个完全二叉树，最后一个节点 n 的父节点为 parent = floor(n/2) (索引从 1 开始);
// 假设父节点的右兄弟存在, 那么父节点的右兄弟 (parent+1) 的左孩子节点为 2x(floor(n/2)+1);
// 当 n 为偶数时, floor(n/2) > (n-1)/2;
// 当 n 为奇数时, floor(n/2) = (n-1)/2,
// 所以 floor(n/2) ≥ (n-1)/2
// 故 2x(floor(n/2)+1) ≥ 2x((n-1)/2+1) = n+1, 而 n 是最大的索引, 故假设不成立
// 与题设矛盾 所以说存储 n 个元素的堆的叶节点的下标分别是 floor(n/2)+1, floor(n/2)+2, ..., n

void build_heap(vector<int> &nums) {
    for (int i = nums.size()/2-1; i >= 0; i--) {
        keep_heap(nums, i);
    }
}

2.循环数组找一个数

解法1

class Solution {
public:
    // 每个元素都不同
    int search(vector<int>& nums, int target) {
        int low = 0;
        int high = nums.size();
        while (low < high) {
            int mid = (low + high) >> 1;
            int median = nums[mid];
            
            if (median == target) return  mid;
            
            if (high-low == 1) break; // 这句话很重要, 即只有一个值时跳出
            
            // low---mid---start---high
            if (median > nums[low]) {  
                if (target > median) {
                    low = mid + 1;
                } else if (target < median) {
                    if (target == nums[low]) {
                        return low;
                    } else if (target > nums[low]) {
                        high = mid;
                    } else {
                        low = mid + 1;
                    }
                }
            } else if (median < nums[low]) {
                 // low---start---mid---high
                if (target < median) {
                    high = mid;
                } else if (target > median) {
                    if (target == nums[low]) {
                        return low;
                    } else if (target > nums[low]) {
                        high = mid;
                    } else {
                        low = mid + 1;
                    }
                }
            }
        }
        
        return -1;
    }
};

解法2

class Solution {
public:
    // 每个元素都不同
    int search(vector<int>& nums, int target) {
        if (nums.empty()) return -1;
        int size = nums.size();
        int lo = 0;
        int hi = size-1;
        
        // 1. 找到旋转点
        // [lo, hi]
        while (hi-lo > 0) {
            int mid = (hi + lo) >> 1;
            if (nums[mid] > nums[hi]) {
                lo = mid + 1;
            } else {
                hi = mid;
            }
        }
        cout << lo << endl;
        
        // 2. 判断 target 在旋转点前半部分还是在旋转点后半部分
        if (target > nums[size-1]) {
            hi = lo;
            lo = 0;
        } else if (target < nums[size-1]) {
            hi = size-1;
        } else {
            return size-1;
        }
        
        // 3. 在有序的部分中, 二分查找
        // [low, high)
        while (hi-lo > 0) {
            int mid = (hi + lo) >> 1;
            if (target == nums[mid]) {
                return mid;
            }
            if (target > nums[mid]) {
                lo = mid + 1;
            } else {
                hi = mid;
            }  
        }
        
        return -1;
    }
        
};

解法3

Let's say nums looks like this:

[12, 13, 14, 15, 16, 17, 18, 19, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]

Because it's not fully sorted, we can't do normal binary search. But here comes the trick:

If target is let's say 14, then we adjust nums to this, where "inf" means infinity:

[12, 13, 14, 15, 16, 17, 18, 19, inf, inf, inf, inf, inf, inf, inf, inf, inf, inf, inf, inf]

If target is let's say 7, then we adjust nums to this:

[-inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]

And then we can simply do ordinary binary search. Of course we don't actually adjust the whole array but instead adjust only on the fly only the elements we look at. And the adjustment is done by comparing both the target and the actual element against nums[0].

class Solution {
public:
    int search(vector<int>& nums, int target) {
        int low = 0;
        int high = nums.size();
        while (low < high) {
            int mid = (high + low) >> 1;
            int median = nums[mid];
            if (median == target) return mid;
            
            if ((target < nums[0]) != (nums[mid] < nums[0])) {
                median = target < nums[0] ? -INFINITY : INFINITY;
            }
            
            if (median < target) {
                low = mid+1;
            } else {
                high = mid;
            } 
        }
        return -1;
    }
};

3.CPU任务分配

一个电脑, 2个 cpu, n 个任务, 所需时间 t, t 为正整数(一个提示), 求完成全部任务的所需最小时间

这样目标转化为将 n 个任务划分为两部分a, b(a ≥ b), 使得 a-b 最小.

设 n 个任务在一个 cpu 上所需时间之和是 sum, sum = a+b

[egin{align*} Target &= min(a-b) \ &= min((sum-b)-b) \ &= min(sum-2b) \ &approx min(frac{sum}{2}-b) ge 0 \ &approx max(b), quad b le leftlfloor{frac{sum}{2}} ight floor end{align*} ]

问题转化:

将 n 个任务取出来, 放在不超过 (leftlfloor{frac{sum}{2}} ight floor)(背包的容量) 的背包里, b 能取得的最大值, 即背包问题. 相对应, 每个任务的时间既代表物品的容量, 也代表物品的价值

#include <iostream>
#include <vector>
using namespace std;
/*
 * 有 N 件物品和一个容量为C的背包, 第i件物品的体积是 W[i]，价值是 V[i]。
 * 求解将哪些物品装入背包可使这些物品的重量总和不超过背包容量，且价值总和最大。
 */
int main () {
    vector<int> weights {4, 6, 2, 2, 5, 1};
    vector<int> values {8, 10, 6, 3, 7, 2};  // output 24
    int total_capacity = 12;
    auto num = weights.size();

    if (total_capacity <= 0) {
        cout << 0 << endl;
        return 0;
    }
    // maximum_value[i][j] 的含义:
    // 将前 i 个物品中的一些物品装入容量为 j 的背包所能产生的最大价值
    vector<vector<int>> maximum_value(num+1, vector<int>(total_capacity+1, 0));
    for (int i_item = 1; i_item < num+1; i_item++) {
        for (int volume = 1; volume <= total_capacity; volume++) {
            if (weights[i_item-1] > volume) {
                maximum_value[i_item][volume] = maximum_value[i_item-1][volume];
            } else {
                maximum_value[i_item][volume] = max(maximum_value[i_item-1][volume],
                                      maximum_value[i_item-1][volume-weights[i_item-1]]
                                      +values[i_item-1]);
            }
        }
    }
    cout << maximum_value[num-1][total_capacity];
    return 0;
}

第四范式笔试

第一题





Example:

Consider the following matrix:

[
  [1,   4,  7, 11, 15],
  [2,   5,  8, 12, 19],
  [3,   6,  9, 16, 22],
  [10, 13, 14, 17, 24],
  [18, 21, 23, 26, 30]
]

Given target = 5, return true.
Given target = 20, return false.

// T(n) = O(m+n)
// S(n) = O(1)
class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        int m = matrix.size();
        if (m == 0) return false;
        int n = matrix[0].size();

        int i = 0, j = n - 1;
        while (i < m && j >= 0) {
            if (matrix[i][j] == target)
                return true;
            else if (matrix[i][j] > target) {
                j--;
            } else 
                i++;
        }
        return false;
    }
};

第二题

二部图概念



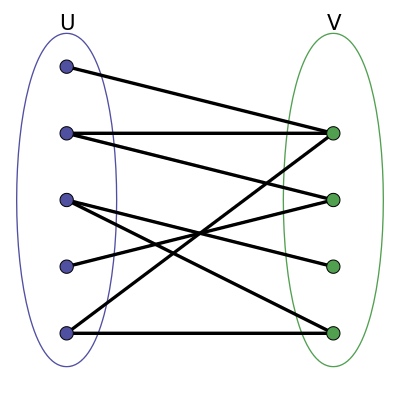
二分图又称双分图、二部图、偶图，指顶点可以分成两个不相交的集 U 和 V, U, V 皆为独立集（independent sets），使得在同一个集内的顶点不相邻（没有共同边）的图。

二分图又称作二部图，是图论中的一种特殊模型。 设 G=(V,E) 是一个无向图，如果顶点 V 可分割为两个互不相交的子集 (U, V)，并且图中的每条边 (i, j) 所关联的两个顶点 i 和 j 分别属于这两个不同的顶点集 (i in U), (j in V)，则称图 G 为一个二分图。

可以将 U 和 V 当做着色图

U 中所有节点为蓝色, V 中所有节点着绿色，每条边的两个端点的颜色不同，符合图着色问题的要求。相反，用这样的着色方式对非二分图是行不通的，根据三角关系：其中一个顶点着蓝色并且另一个着绿色后，三角形的第三个顶点与上述具有两个颜色的顶点相连，无法再对其着蓝色或绿色(即非二分图, 存在一个顶点既属于 U, 又属于 V)。

解题思路

根据二分图的特性，一条边上的两个点，肯定是属于不同的组。如果它们出现在同一个组中，肯定就不是二分图了。

怎么判断，一条边上的两个点，分属于不同的组呢？

我们需要遍历图，如果找到一条边，两个节点，都在同一组，则不是二分图；如果图遍历完成之后，没有找到这样的边，则是二分图。我们在遍历的过程中，我们需要区分，一条边的两个节点分属于不同的组，这里我们用到了染色法。

核心思想如下：

从某一个点开始，将这个节点染色为白色，并且开始广度优先遍历，找到与其相邻的节点，如果是二分图，相邻节点的颜色都应该不同。如果是黑色，则不变；如果是无色，则染成黑色；如果是白色，也就是同色，程序退出。当图遍历完毕时，没有相邻节点同色的，则是二分图，标记为白色和黑色的两组就是一个划分。



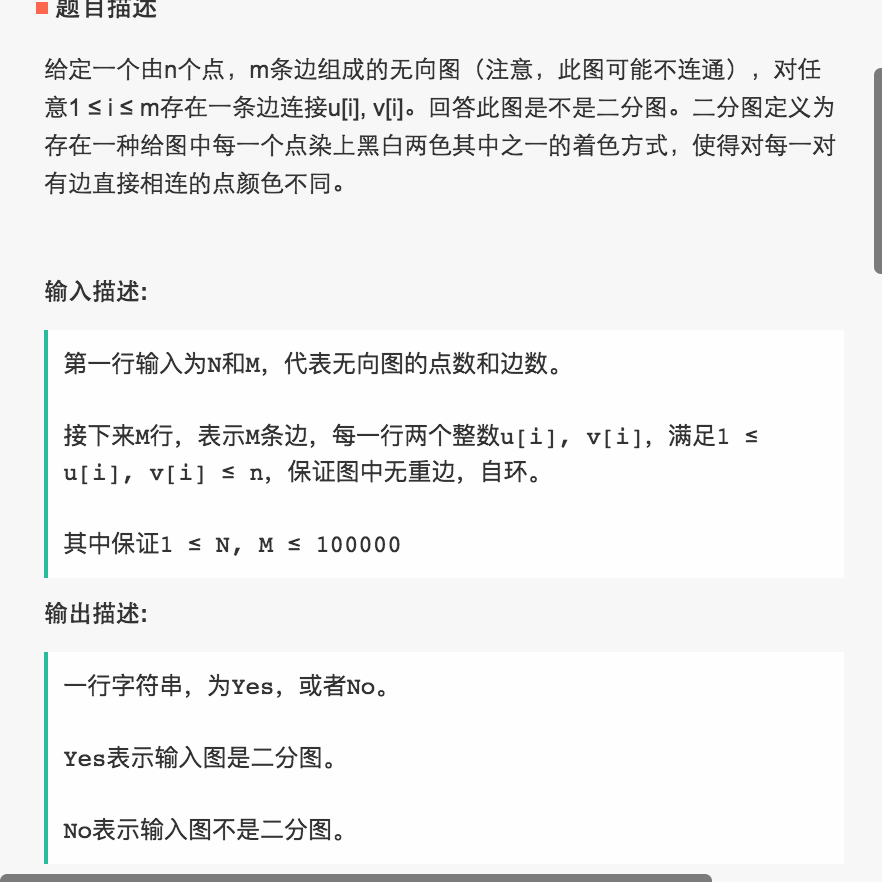
input:
5 6
1 2
2 3
3 4
4 1
4 5
5 2

output:
Yes

input:
5 4
1 2
2 3
3 1  
4 5

output:
No
解释: 有三角形存在.

#include <queue>
#include <iostream>
using namespace std;

bool isBipartiteGraph(vector<vector<int>> &graph,
                      vector<int> &color, int vertex) {
    queue<int> mq;
    mq.push(vertex);
    // 对于还未被染色 vertex, 设置为 1 或者为 0 都可以, 这是由于该 vertex 已经在第二个连通图中
    // 如果 vertex 还在之前的连通图中的话,
    // 那么该 vertex 一定会被遍历, 所以该 vertex 不在之前的连通图中.
    color[vertex] = 1;
    while(!mq.empty()) {
        int from = mq.front();
        mq.pop();
        for(auto to : graph[from]) {
            if (color[to] == -1) {
                color[to] = !color[from]; //染成不同的颜色, 使用!求反, 很骚气
                mq.push(to);
            } else {
                if (color[from] == color[to]) {
                    return false;  // 颜色相同，则不是二分图
                }
            }
        }
    }
    return true;
}

// 使用邻接链表要方便点
int main() {
    int num_vertex, num_edge;
    cin >> num_vertex >> num_edge;
    vector<vector<int>> adjList(num_vertex);
    vector<int> color(num_vertex, -1);
    int u, v;
    for(int i = 0; i < num_edge; i++) {
        cin >> u >> v;
        adjList[u-1].push_back(v-1);
    }

    for(int i = 0; i < num_vertex; i++)
        // 如果该节点还未被遍历
        if(color[i] == -1 ) {
            if (!isBipartiteGraph(adjList, color, i)) {
                cout << "No" <<endl;
                return 0;
            }
        }
    cout << "Yes" <<endl;

    return 0;
}