Convolutional Neural Networks backpropagation: from intuition to derivation
这里假设你已经对多层感知器、损失函数、反向传播等有一定掌握,如果还没有了解过,最好先去了解一下
开篇
Convolutional Neural Networks(CNN)现在是做图像分类的标准方式,现在已经有许多开源的深度学习框架、训练好的模型和服务等,配置框架环境所花的时间甚至比真正开始做图像分类的时间还多。同时,现在已经有许多网课和电子书让你去直接了解和使用这些强大深度学习思想,“零距离接触”吴恩达大佬、Yoshua Bengio、Yann Lecun等,跟随他们的步伐进行学习
然而当我要深入了解CNN的时候,我发现找不到“CNN反向传播——笨蛋也看得懂的教程”等类似的文章。更多的我找到的是“如果你了解过标准神经网络中的反向传播,那CNN中的反向传播对你来说肯定不成问题”或者是“除了矩阵乘法变成了卷积,其它的都一样”。。。当然,我也见过许多已经推导好的数学公式,但是对于新手不友好啊
让我感到安慰的是,我发现我并不是一个人!比如我看到有人问:Hello,为什么计算CNN中的梯度的时候要把权值进行旋转?
别着急,这个问题的答案将在下面这篇长文给出
正文
我们刚开始都是从多层感知器开始入门,并且根据教程小心翼翼地计算误差
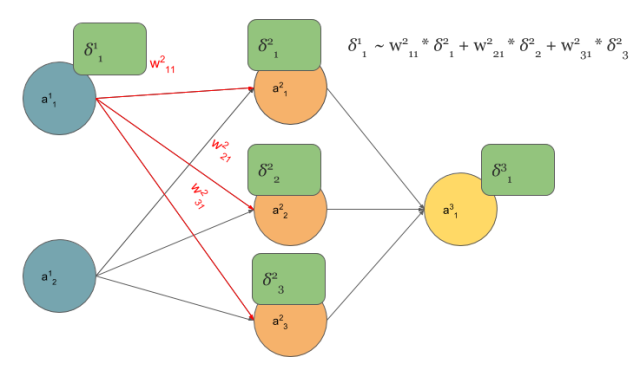
从图中可以看到最左上角的单元,其“看到”的梯度\(\delta^1_1\)与下一层三个单元"看到"的梯度乘上相应的三个权值之和成正比,也就是图中的式子
但我们怎么将多层感知器(MLP)的概念与CNN联系起来呢,看下面的将MLP转化为CNN:

如果你依然对这个过程感到不明觉厉,也就是对connections cutting和weights sharing的概念感到不明觉厉,我觉得下面这张图(CNN中的正向传播)会对你有点启发

也就是说右边这种神经网络和左边的二维卷积操作结果是相同的,其中的权值只是作为滤波器filters(也叫作核kernels、卷积矩阵convolution matrices、masks)
现在回到计算梯度,但这次我们把注意力放在CNN的梯度计算上来,见下图(反向传播也需要卷积)

这图是不是很熟悉呢,是的就是之前介绍的MLP反向传播过程,现在结合到了CNN中,自行体会一下。下面可以开始讲讲卷积了...

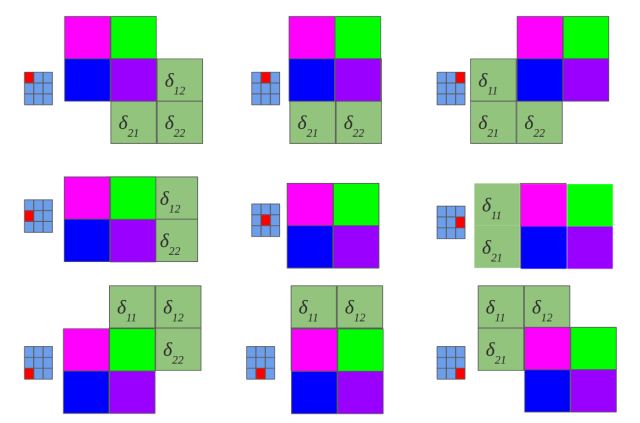
看起来与之前的前向传播不太一样。之前我们做的是"valid convolution",这里我们做了"full convolution"(命名法见此)。另外,我们还把卷积核旋转了180°
现在:
- 在正向和反向传播中,矩阵点乘都变成了卷积运算
- 在继续之前,我们要证明上面的过程
在标准的MLP中,我们对神经元j的误差定义为
\(\delta^l_j = \frac{\partial C}{\partial z^l_j}\)
其中\(z^l_j = \sum_k {w^l_{jk}a^{l-1}_k+b^l_j}\)
为了表达得更清楚些,\(a^l_j=\sigma(z^l_j)\),其中的激活函数可以是simoid,tanh或者relu等
但在CNN中,我们不用MLP矩阵乘法,而是用卷积(符号为*)。所以我们用\(z_{x,y}\)来表示线性输出,因为是二维卷积,其中x,y分别表示行和列
\(z^{l+1}_{x,y}=w^{l+1}*\sigma(z^l_{x,y})+b^{l+1}_{x,y}=\sum_a\sum_b w^{l+1}_{a,b}\sigma(z^l_{x-a,y-b})+b^{l+1}_{x,y}\)
上面的式子就是在CNN在正向传播中进行的卷积操作
现在我们可以继续探讨一开始提出的问题:Hello,为什么计算CNN中的梯度的时候要把权值进行旋转?
看到下面的式子:
\(\delta^l_{x,y}=\frac{\partial C}{\partial z^{l+1}_{x',y'}}=\sum_{x'}\sum_{y'}\frac{\partial C}{\partial z^{l+1}_{x',y'}}\frac{\partial z^{l+1}_{x',y'}}{\partial z^l_{x,y}}\)
我们知道\(z^l_{x,y}\)与\(z^{l+1}_{x',y'}\)是相关的,通过上面“反向传播也需要卷积”这张图片。所以上面等式就是链式求导法则的结果,让我们接着往下看(latex太他妈长了,不写了):
式子好像变得更长了,不用担心,这里只是把\(z^{l+1}_{x',y'}\)代入了式子而已,后面你会发现十分方便化简。观察式子,由于前面的求和符号可以看成是对下一层的每个单元遍历,而观察最左边的偏导,偏导的分子除了\(x'-a=x, y'-b=y\)的位置以外,其它的\(x'\)和\(y'\)取值对\(z^l_{x,y}\)偏导都为0,所以又可以化简为以下的式子
如果和
那么显然有
与
,所以又可以写成
OK,最终式子化成了
所以说好的权值旋转180°呢??,实际上,
这里补充一下:卷积数学公式中的减号,在二维矩阵的场景下,可以被解释为:先旋转、再相乘。由于在深度学习中,核矩阵是一个需要训练的参数,卷积神经网络都是针对图像,图像即使旋转180度,对于计算机来说区别不大。旋转与否,或者说是否使用减号,对于深度学习来说关系不大,反而不旋转的互相关运算计算起来更方便。因此,很多深度学习框架直接使用互相关运算来表示卷积的过程。
同时,互相关与卷积的区别,可以简单看下这篇教程https://lulaoshi.info/machine-learning/convolutional/two-dimension-convolution-layer
如果之前一直看的是ng的深度学习视频,会发现他一直在使用的“卷积”其实是互相关,而这篇博客中的卷积是就是卷积的定义
所以问题的答案很简单:权值的旋转只是CNN反向传播求导中某步的化简结果
最后,反向传播还有一步:参数的更新,下面给出最终的参数求导公式(根据上面的推导):
总结
最后,CNN的反向传播算法总结如下:
- 输入x,对输入层设置合适的激活函数
- 正向传播:对每层计算线性部分\(z^l_{x,y}=w^l*\sigma(z^{l-1}_{x,y})\)和非线性部分\(a^l_{x,y}=\sigma(z^l_{x,y})\),像MLP那样,只不过矩阵乘法变成了卷积运算
- 计算最后一层的导数
- 反向传播
- 得出参数的导数