* @Description 将一条绳子剪成任意 m 段,m 大于 1 ,求最大积
* 决定问题规模的参数为绳子的长度 n
* 按 n 进行分治,G( n ) 为长度为 n 的绳子分割后可得的最大积,可列出状态转移方程:
* G( n ) = max { G(n-1)*1 , G(n-2)*2...G(1)*(n-1) , n }
* 之所以最后还有一个 n ,是考虑要覆盖到不分段时的结果
* 但是在第一次分段,也就是对完整的绳子分段时不能考虑 n ,因为 m 大于 1,这里要做特殊处理
递归描述:
public int cuttingRope0(int flag, boolean isRoot, int[] cache) { if (flag == 1) { return 1; } if (cache[flag] != 0) { return cache[flag]; } int max = 0; for (int i = 1; i <= flag; i++) { int re = cuttingRope0(flag - i, false, cache); max = Math.max(qmul_mod(re,i,1000000007), max); } if (!isRoot) { max = Math.max(max, flag); } cache[flag] = max; return max; }
结果没有问题,但是未对大数取模。我们将其优化为递推描述,并添加取模逻辑:
public int cuttingRope(int n) { if (n < 2) { return n; } BigInteger[] cache = new BigInteger[n + 1]; cache[1] = new BigInteger("1"); for (int i = 2; i <= n; i++) { for (int j = 1; j <= i; j++) { BigInteger re = cache[i - j].multiply(new BigInteger(String.valueOf(j))); cache[i] = cache[i].max(re); } if (i != n) { cache[i] = cache[i].max(new BigInteger(String.valueOf(i))); } } return cache[n].mod(new BigInteger("1000000007")).intValue(); }
这里我们直接使用了 BigInteger 类进行大数运算,除此之外我们也可以借助快速乘取模算法进行 int 的取模。
快速乘取模算法的思路是,对于 a*b ,我们可以将 b 看做一个二进制数。
比如 9:
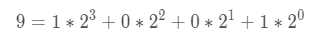
那么 a*9 可以转化为:

我们对 a ,b 不断进行右移、左移操作分步进行计算。快速乘:
public static int qmul_num(int a, int b) { int ans = 0; while (b != 0) { if ((b & 1) != 0) { ans += a; } b >>= 1; a <<= 1; } return ans; }
快速乘配合取模:
public static int qmul_mod(int a, int b, int mod) { int ans = 0; while (b != 0) { if (((b %= mod) & 1) != 0) { ans += a %= mod; } b >>= 1; a <<= 1; } return ans % mod; }