题目描述
如果对某个图进行变换,使得原来任意两个有连线的顶点之间都不再有连线,原来任意两个没有连线的顶点之间现在都有连线了,那么所得到的图就是原来那个图的“补图”。
而两个图互补是指在对第二个图进行重标号后可以使其成为第一个图的补图。
而一个图是自补图当且仅当其与自身互补。
现在你需要对给定的 n给出一个点数为 n 的自补图构造,或者告知不存在。
输入格式
输入一行一个正整数 n(1≤n≤2000).
输出格式
如果不能一个点数为 n 的自补图,你输出 NO。
否则输出一行 YES。
接下来若干行,每行有两个正整数 x,y(x≠y),表示在你的构造中有一条 x−y 的边。
最后一行输出一个n排列,表示让这个图成为自身补图的重标号方式。
你只需输出任意一个满足条件的图即可。
------------------------------------------------------分割线------------------------------------------------------
一看这道题,第一思路很明显是打表。。。
如果您觉得 :1. 我能手推打出一个2000的表---很明显您可以不看接下来的内容了
2.我能手推打出一个10的表----那您能很容易的看懂以下内容
3.我能想出正解---请不要吐槽我XX的做法
------------------------------------------------------分割线------------------------------------------------------
进入正题:
我们不难看出,如果只是在一个图上变化点,将两个图重叠在一起是一个完全图(任意两个点之间有一条边)
那很明显,边的数量应该是个偶数,因此先判断n(n-1)%4是否==0,如果!=0,直接NO
那么,我们思考一下,如果想让重新编号能够互补的话,最好想的方法就是使其对称(反正是Special Judge)
则我们就可以先将图一分为二(分成奇数和偶数分别考虑)
举个例子:

这样是奇数的情况(9):然后我们将右半部分(5)个的点构建一个完全图,然后保持E点不动,将A,B,C,D全部换到左边,并使F,G,H,I全部变到右边
并在中途使F,G,H,I互不相连,即将F,G,H,I全连到右半部分,那我们来算一下左边应该连几条边,我们计算一下,每一个点应该连(n-1)/4条边(具体计算动动笔就好)
那我们考虑怎样才能让在连完边后更简单的找到变换点
然后我们有了一个比较流氓的做法:
我们发现很明显右边的点总是比左边的点多一个,那我们就固定这个E点不动,这样两边的点就一样了;
更进一步,左右(现在)的点都为偶数(去掉E点后),这样,我们再将左右两边各再分成两半,可以发现每一部分正好是(n-1)/4这样我们可以让左右上下交叉相连:
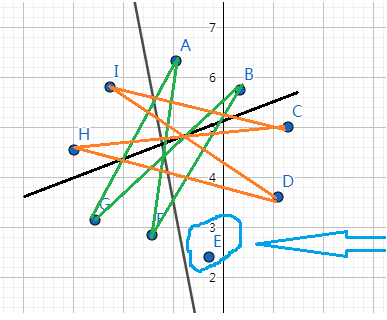
有点乱。。。
这样,我们重建的时候只需要将左边正序,右边倒序就可以(这个画画图就能退出来了),即输出 F ,G ,H ,I ,E ,D ,C ,B ,A
是不是很好理解??
这样奇数就解决了;
------------------------------------------------------分割线------------------------------------------------------
那么偶数呢??
我们只需要去掉那个特殊点就好了
同理不写了QWQ
那最后上个代码,时间复杂度应该不太到O(n2)??
#include<cstdio>
using namespace std;
int path[5050][5050];
int n;
int work1()
{
for(int i=1;i<=((n+1)/2);i++)
{
for(int j=i+1;j<=((n+1)/2);j++)
{
path[i][j]=1;
}
}
int l=(n-1)/4+(n+1)/2;
for(int u=(n+1)/2+1;u<=n;u++)
{
if(u<=l)
for(int j=1;j<=(n-1)/4;j++)
path[u][j]=1;
else
for(int j=(n-1)/4+1;j<=(n+1)/2-1;j++)
path[u][j]=1;
}
printf("YES
");
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
if(path[i][j]==1)
{
printf("%d %d
",i,j);
}
}
}
for(int i=(n+1)/2+1;i<=n;i++)
{
printf("%d ",i);
}
for(int i=(n+1)/2;i>=1;i--)
{
printf("%d ",i);
}
return 0;
}
int work2()
{
for(int i=1;i<=(n/2);i++)
{
for(int j=i+1;j<=(n/2);j++)
{
path[i][j]=1;
}
}
int l=n/4+n/2;
for(int u=n/2+1;u<=n;u++)
{
if(u<=l)
for(int j=1;j<=n/4;j++)
path[u][j]=1;
else
for(int j=(n/4+1);j<=(n/2);j++)
path[u][j]=1;
}
printf("YES
");
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
if(path[i][j]==1)
{
printf("%d %d
",i,j);
}
}
}
for(int i=n/2+1;i<=n;i++)
{
printf("%d ",i);
}
for(int i=n/2;i>=1;i--)
{
printf("%d ",i);
}
return 0;
}
int main()
{
scanf("%d",&n);
if(n*(n-1)%4!=0) printf("NO
");
else
{
if(n%2==1)
work1();
else
work2();
}
return 0;
}
有错在评论区直接写出就行QWQ
