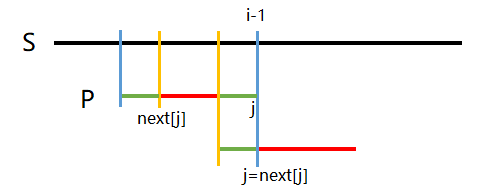算法介绍
KMP算法是一种改进的字符串匹配算法,由D.E.Knuth,J.H.Morris和V.R.Pratt提出的,因此人们称它为克努特—莫里斯—普拉特操作(简称KMP算法)。KMP算法的核心是利用匹配失败后的信息,尽量减少模式串与主串的匹配次数以达到快速匹配的目的。具体实现就是通过一个next()函数实现,函数本身包含了模式串的局部匹配信息。KMP算法的时间复杂度O(m+n)。
next数组
我们记主串为字符串S,模式串为字符串P。
我们用next[j]表示以字符Pj结尾的子串的长度相等的前缀字符串与后缀字符串长度的最大值。
特别地,当没有满足条件的子串时,next[j] = 0。
为了方便起见,我们将字符串从下标1开始匹配。如此,next数组所表示的长度就与下标数值相等了。
算法思路
我们从左到右依次枚举S的每一个字符Si,对于当前待匹配字符Si,我们假设当前P字符串中已匹配到Pj。
那么我们只需判断Si和Pj+1,若两者相同,则继续匹配。
若两者不相同,那么我们使j=next[j],即可最大限度的减少匹配次数。因为S字符串的从某位置开始到前i-1的部分与P字符串的前j个字符已匹配(即完全相同),如图中两蓝色直线所夹的S、P的两段,而P1到Pnext[j]部分是长度最大的与以Pj结尾的后缀完全相同的前缀(图中绿色线段),而该以Pj结尾的后缀则必定与S中一段以Si-1结尾的子串完全相同,因而保证了上述操作的正确性。
接下去只需重复上述操作即可。
而对于next数组的预处理,也同上述操作类似,我们只需要以字符串P来匹配字符串P即可。
模板呈现
模板题链接:KMP字符串
代码如下:
#include <iostream> #include <algorithm> #include <cstdio> using namespace std; const int M = 1e5+10; int n,m; int ne[M]; char s[M],p[M]; int main() { cin>>n>>p+1; cin>>m>>s+1; for(int i=2,j=0;i<=n;i++) { while(j && p[i]!=p[j+1])j=ne[j]; if(p[i]==p[j+1])j++; ne[i]=j; } for(int i=1,j=0;i<=m;i++) { while(j && s[i]!=p[j+1])j=ne[j]; if(s[i]==p[j+1])j++; if(j==n) { printf("%d ",i-n+1-1); j=ne[j]; //可有可无,好习惯要加上。若为string,不加会出错。 } } printf(" "); return 0; }