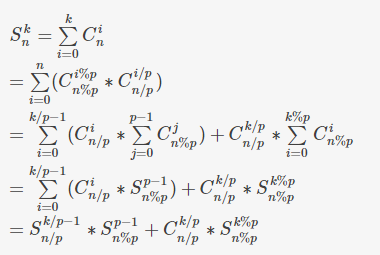Link:
Solution:
记录一下推$sum_{i=0}^k C_n^i$的过程:
其实就是将相同的$i/p$合起来算,这样每个里面都是一个可以预处理的子问题
接下来递归下去算即可
Tip:推式子时尽量化出与模数相关的量方便预处理
Code:
#include <bits/stdc++.h> using namespace std; #define X first #define Y second #define pb push_back typedef double db; typedef long long ll; typedef pair<int,int> P; int T;const int MOD=2333; ll C[MOD+10][MOD+10],sum[MOD+10][MOD+10]; ll Lucas(ll x,ll y) { if(y==0) return 1; return Lucas(x/MOD,y/MOD)*C[x%MOD][y%MOD]%MOD; } ll cal(ll n,ll k) { if (k<0) return 0; return (cal(n/MOD,k/MOD-1)*sum[n%MOD][MOD-1]+Lucas(n/MOD,k/MOD)*sum[n%MOD][k%MOD])%MOD; } int main() { C[0][0]=1;sum[0][0]=1; for (int i=1;i<MOD;i++) sum[0][i]=1; for (int i=1;i<MOD;i++) { C[i][0]=sum[i][0]=1; for (int j=1;j<=i;j++) C[i][j]=(C[i-1][j-1]+C[i-1][j])%MOD; for (int j=1;j<MOD;j++) sum[i][j]=(sum[i][j-1]+C[i][j])%MOD; } scanf("%d",&T); while (T--) { ll n,k; scanf("%lld%lld",&n,&k); printf("%lld ",cal(n,k)); } return 0; }