ELGamal密码
ELGamal密码是除了RSA之外最有代表性的公开密钥密码之一,它的安全性建立在离散对数问题的困难性之上,是一种公认安全的公钥密码。
离散对数问题
设p为素数,若存在一个正整数α,使得α、α2、...、αp-1关于模p互不同余,则称α为模p的一个原根。于是有如下运算:
α的幂乘运算:
y=αx(mod p),1≤x≤p-1
α的对数运算:
x=logαy,1≤y≤p-1
只要p足够大,求解离散对数问题时相当复杂的。离散对数问题具有较好的单向性。
ELGamal加解密算法
1.随机地选择一个大素数p,且要求p-1有大素数因子,将p公开。
2.选择一个模p的原根α,并将α公开。
3.随机地选择一个整数d(1<d<p-1)作为私钥,并对d保密。
4.计算公钥y=αd(mod p),并将y公开。
加密
1.随机地选取一个整数k(1<k<p-1)。
2.计算U=yk(mod p)、C1=αk(mod p)、C2=UM(mod p)。
3.取(C1,C2)作为密文。
解密
1.计算V=C1d(mod p)。
2.计算M=C2V-1(mod p)。
ELGamal算法细节
实现ELGamal算法,需要实现以下几个部分:
1.对大数的素数判定;
2.判断原根;
3.模指运算;
4.模逆运算。
判断原根
已知a和m互素,如果d是满足ad=1(mod m)的最小正整数,则称d为a模m的阶,记为d=σm(a)。由于a和m互素,根据欧拉定理可知aφ(m)=1(mod m),由此可以得到σm(a) | φ(m)。
若a是m的原根,则σm(a)=φ(m)。
根据上述两点,推出逆否命题:如果∃d | φ(m)且d≠φ(m),使得ad=1(mod m),则a不是模m的原根。所以判断a是否为模m的原根,最快的方法就是判断φ(m)的每一个因子d是否使得ad=1(mod m)。如果满足ad=1(mod m)的d=φ(m),则a是模m的原根。
e.m.判断2是不是模11的原根
φ(11)=10
10的因子有1、2、5、10,所以:
2(mod 11)=2
22(mod 11)=4
25(mod 11)=10
210(mod 11)=1
因此,2是模11的原根。
ELGamal密码的安全性
由于ELGamal密码的安全性建立在GF(p)上离散对数的困难性之上,而目前尚无求解GF(p)上离散对数的有效算法,所以在p足够大时ELGamal密码是安全的。理想情况下p为强素数,p-1=2q,q为大素数。
为了安全加密所使用的k必须是一次性的。如果长期使用同一个k加密的话,就可能被攻击者获取,从而根据V=U=yk(mod p),M=C2V-1(mod p)而得到明文。另外,使用同一个k加密不同的明文M和M',则由于
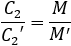
如果攻击者知道M,则很容易求出M'。此外,k选取时还要保证U=yk(mod p)≠1。
Java实现
ELGamal
1 do { 2 p = BigInteger.probablePrime(100, new Random()); 3 } while (p.subtract(BigInteger.ONE).divide(new BigInteger("2")).isProbablePrime(100)); 4 do { 5 alpha = new BigInteger(100, new Random()); 6 } while (! isOrigin(alpha, p)); 7 do { 8 d = new BigInteger(100, new Random()); 9 } while (d.compareTo(BigInteger.ONE) != 1 || d.compareTo(p.subtract(BigInteger.ONE)) != -1); 10 y = alpha.modPow(d, p);
1 /** 2 * 加密 3 * @param M 4 * @return 5 */ 6 BigInteger[] encrypt(BigInteger M) { 7 BigInteger[] C = new BigInteger[2]; 8 BigInteger k, U; 9 do { 10 do { 11 k = new BigInteger(100, new Random()); 12 } while (k.compareTo(BigInteger.ONE) != 1 || k.compareTo(p.subtract(BigInteger.ONE)) != -1); 13 U = y.modPow(k, p); 14 } while (U.intValue() != 1); 15 C[0] = alpha.modPow(k, p); 16 C[1] = U.multiply(M).mod(p); 17 return C; 18 }
1 /** 2 * 解密 3 * @param C 4 * @return 5 */ 6 BigInteger decrypt(BigInteger[] C) { 7 BigInteger V = C[0].modPow(d, p); 8 BigInteger M = C[1].multiply(V.modPow(new BigInteger("-1"), p)).mod(p); 9 return M; 10 }
判断原根
1 /** 2 * 判断a是否为模m的原根,其中m为素数 3 * @param a 4 * @param m 5 * @return 6 */ 7 static boolean isOrigin(BigInteger a, BigInteger m) { 8 if (a.gcd(m).intValue() != 1) return false; 9 BigInteger i = new BigInteger("2"); 10 while (i.compareTo(m.subtract(BigInteger.ONE)) == -1) { 11 if (m.mod(i).intValue() == 0) { 12 if (a.modPow(i, m).intValue() == 1) 13 return false; 14 while (m.mod(i).intValue() == 0) 15 m = m.divide(i); 16 } 17 i = i.add(BigInteger.ONE); 18 } 19 return true; 20 }
测试
测试数据
p=2579
α=2
d=765
M=1299
k=853
测试结果

参考文献
张焕国,唐明.密码学引论(第三版).武汉大学出版社,2015年