我们使用的浏览器都有前进、后退功能。譬如:当你依次访问完一串页面 a-b-c 之后,点击浏览器的后退按钮,就可以查看之前浏览过的页面 b 和 a。当你后退到页面 a,点击前进按钮,就可以重新查看页面 b 和 c。但是,如果你后退到页面 b 后,点击了新的页面 d,那就无法再通过前进、后退功能查看页面 c 了。
实现这个功能,就要借助“栈”这个数据结构。
一、如何理解“栈”
关于“栈”,我有一个非常贴切的例子,就是一摞叠在一起的盘子。我们平时放盘子的时候,都是从下往上一个一个放;取的时候,我们也是从上往下一个一个地依次取,不能从中间任意抽出。后进先出,先进后出,这就是典型的“栈”结构。
从栈的操作特性上来看,栈是一种“操作受限”的线性表,只允许在一端插入和删除数据。
这种操作受限的特性,可能会让我们疑惑——和数组与链表相比,栈平添了限制,似乎没有任何优势。直接使用数组或者链表不香吗?为什么还要用这个“操作受限”的“栈”呢?
从功能上来说,数组或链表确实可以替代栈。但我们一定要建立一个观念:特定的数据结构是对特定场景的抽象。此外,数组或链表暴露了太多的操作接口,操作灵活自由的同时,不可控性也更大,出错的可能也随之增大。这其实和 Linux 的文件权限类似,777 权限最宽松,但安全性更低。
当某个数据集合只涉及在一端插入和删除数据,并且满足后进先出、先进后出的特性,我们就应该首选“栈”这种数据结构。
二、如何实现一个“栈”
栈的主要操作
从刚才栈的定义里,我们可以看出,栈主要包含两个操作:
- 入栈:在栈顶插入一个数据
- 出栈:从栈顶删除一个数据
如何实现栈
栈既可以用数组来实现,也可以用链表来实现。
- 顺序栈:用数组实现的栈;
- 链式栈:用链表实现的栈。
顺序栈
下面这段 Java 代码用数组实现了顺序栈:
1 // 基于数组实现的顺序栈 2 public class ArrayStack { 3 private String[] items; // 数组 4 private int count; // 栈中元素个数 5 private int n; //栈的大小 6 7 // 初始化数组,申请一个大小为n的数组空间 8 public ArrayStack(int n) { 9 this.items = new String[n]; 10 this.n = n; 11 this.count = 0; 12 } 13 14 // 入栈操作 15 public boolean push(String item) { 16 // 数组空间不够了,直接返回false,入栈失败。 17 if (count == n) return false; 18 19 // 将item放到下标为count的位置,并且count加一 20 items[count] = item; 21 ++count; 22 return true; 23 } 24 25 // 出栈操作 26 public String pop() { 27 // 栈为空,则直接返回null 28 if (count == 0) return null; 29 30 // 返回下标为count-1的数组元素,并且栈中元素个数count减一 31 String tmp = items[count-1]; 32 --count; 33 return tmp; 34 } 35 }
链式栈
1 public class LinkedListStack { 2 3 private Node top = null; 4 5 public void push(int newValue) { 6 Node newNode = new Node(newValue, null); 7 8 if (top == null) { 9 top = newNode; 10 } else { 11 newNode.next = top; 12 top = newNode; 13 } 14 } 15 16 public int pop() { 17 if (top == null) { 18 System.out.println("The stack is empty!"); 19 return -1; 20 } 21 22 int tmp = top.getData(); 23 24 top = top.next; 25 26 return tmp; 27 } 28 29 private class Node { 30 31 private int data; 32 private Node next; 33 34 public Node(int data, Node next) { 35 this.data = data; 36 this.next = next; 37 } 38 39 public int getData() { 40 return this.data; 41 } 42 } 43 }
栈的时间复杂度
不管是顺序栈还是链式栈,入栈、出栈只涉及栈顶个别数据的操作,所以时间复杂度都是 O(1)。
栈的空间复杂度
不管是顺序栈还是链式栈,存储数据只需要一个大小为 n 的数组或链表。在入栈和出栈过程中,只需要一两个临时变量存储空间,所以空间复杂度是 O(1)。
这里可能会造成困惑——存储数据需要一个大小为 n 的数组或链表,那么空间复杂度不应该是 O(n) 吗?这个概念一定要搞清楚,说空间复杂度的时候,是指除了原本的数据存储空间外,算法运行还需要额外的存储空间。数组或链表这个大小为 n 的空间是必须的,无法省掉。
三、支持动态扩容的顺序栈
在前面的示例中,我们实现了基于数组的顺序栈。顺序栈的大小是固定的,需要在初始化栈时事先指定。当顺序栈满了之后,就无法再往栈里添加数据了。链式栈的大小不受限,但要存储 next 指针,内存消耗相对较多。我们如何基于数组实现一个可以支持动态扩容的栈呢?
在数组那一节,我们提到过支持动态扩容的数组。基本思想是:当数组空间不够时,我们就重新申请一块更大的内存,将原来数组中数据统统拷贝过去。这样就实现了一个支持动态扩容的数组。
要实现一个支持动态扩容的栈,只要底层依赖一个支持动态扩容的数组就可以了。当栈满了之后,我们就申请一个更大的数组,将原来的数据搬移到新数组中。图示如下:
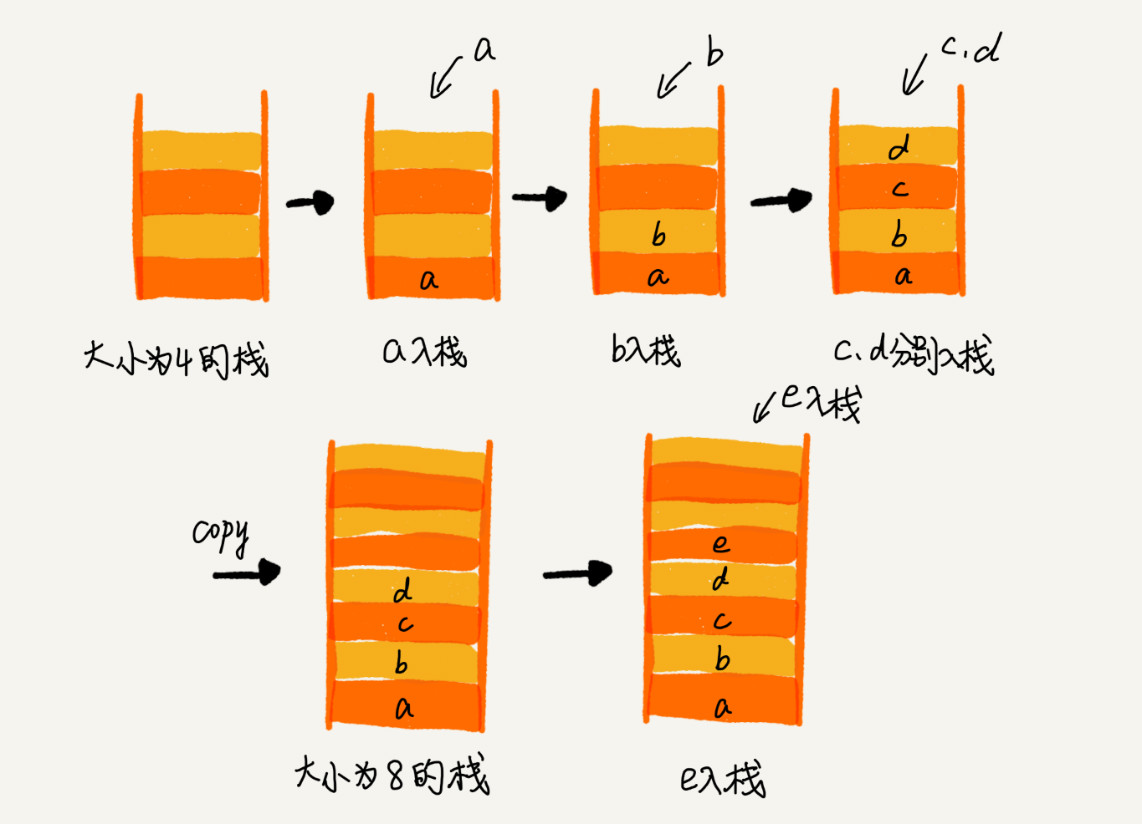
实际开发中很少用到支持动态扩容的顺序栈。对于这个问题,我们重点是复杂度分析。
对于出栈操作来说,我们不会涉及内存的重新申请和数据的搬移,所以出栈的时间复杂度仍然是 O(1)。但是,对于入栈操作来说,情况就不一样了。当栈中有空闲空间时,入栈操作的时间复杂度为 O(1)。但当空间不够时,就需要重新申请内存和数据搬移,所以时间复杂度就变成了 O(n)。
也就是说,对于入栈操作来说,最好情况时间复杂度是 O(1),最坏情况时间复杂度是 O(n)。那平均情况下的时间复杂度又是多少呢?还记得我们在复杂度分析那一节中讲的摊还分析法吗?这个入栈操作的平均情况下的时间复杂度可以用摊还分析法来分析。我们也正好借此来实战一下摊还分析法。
为了分析的方便,我们需要事先做一些假设和定义:
- 栈空间不够时,我们重新申请一个是原来大小两倍的数组;
- 为了简化分析,假设只有入栈操作没有出栈操作;
- 定义不涉及内存搬移的入栈操作为 simple-push 操作,时间复杂度为 O(1)。
如果当前栈大小为 K,并且已满,当再有新的数据要入栈时,就需要重新申请 2 倍大小的内存,并且做 K 个数据的搬移操作,然后再入栈。但是,接下来的 K-1 次入栈操作,我们都不需要再重新申请内存和搬移数据,所以这 K-1 次入栈操作都只需要一个 simple-push 操作就可以完成。为了让你更加直观地理解这个过程,我画了一张图。

你应该可以看出来,这 K 次入栈操作,总共涉及了 K 个数据的搬移,以及 K 次 simple-push 操作。将 K 个数据搬移均摊到 K 次入栈操作,那每个入栈操作只需要一个数据搬移和一个 simple-push 操作。以此类推,入栈操作的均摊时间复杂度就为 O(1)。
通过这个例子的实战分析,也印证了前面讲到的,均摊时间复杂度一般都等于最好情况时间复杂度。因为在大部分情况下,入栈操作的时间复杂度 O 都是 O(1),只有在个别时刻才会退化为 O(n),所以把耗时多的入栈操作的时间均摊到其他入栈操作上,平均情况下的耗时就接近 O(1)。
四、栈在函数调用中的应用
前面的内容比较偏理论,我们接下来看看,栈在软件工程中的实际应用。栈作为一个比较基础的数据结构,应用场景还是蛮多的。比较经典的一个应用场景就是函数调用栈。
操作系统给每个线程分配了一块独立的内存空间,这块内存被组织成“栈”这种结构, 用来存储函数调用时的临时变量。每进入一个函数,就会将临时变量作为一个栈帧入栈,当被调用函数执行完成,返回之后,将这个函数对应的栈帧出栈。为了让你更好地理解,我们一块来看下这段代码的执行过程。
1 int add(int x, int y) 2 { 3 int sum = 0; 4 sum = x + y; 5 6 return sum; 7 } 8 9 int main() 10 { 11 int a = 1; 12 int ret = 0; 13 int res = 0; 14 15 ret = add(3, 5); 16 res = a + ret; 17 printf("%d", res); 18 19 reuturn 0; 20 }
从代码中我们可以看出,main() 函数调用了 add() 函数,获取计算结果,并且与临时变量 a 相加,最后打印 res 的值。为了让你清晰地看到这个过程对应的函数栈里出栈、入栈的操作,我画了一张图。图中显示的是,在执行到 add() 函数时,函数调用栈的情况。

五、栈在表达式求值中的应用
我们再来看栈的另一个常见的应用场景,编译器如何利用栈来实现表达式求值。
为了方便解释,我将算术表达式简化为只包含加减乘除四则运算,比如:34+13*9+44-12/3。对于这个四则运算,我们人脑可以很快求解出答案,但是对于计算机来说,理解这个表达式本身就是个挺难的事儿。如果换作你,让你来实现这样一个表达式求值的功能,你会怎么做呢?
实际上,编译器就是通过两个栈来实现的。其中一个保存操作数的栈,另一个是保存运算符的栈。我们从左向右遍历表达式,当遇到数字,我们就直接压入操作数栈;当遇到运算符,就与运算符栈的栈顶元素进行比较。
如果比运算符栈顶元素的优先级高,就将当前运算符压入栈;如果比运算符栈顶元素的优先级低或者相同,从运算符栈中取栈顶运算符,从操作数栈的栈顶取 2 个操作数,然后进行计算,再把计算完的结果压入操作数栈,继续比较。
我将 3+5*8-6 这个表达式的计算过程画成了一张图,你可以结合图来理解我刚讲的计算过程。

六、栈在括号匹配中的应用
除了用栈来实现表达式求值,我们还可以借助栈来检查表达式中的括号是否匹配。
我们同样简化一下背景。我们假设表达式中只包含三种括号,圆括号 ()、方括号[]和花括号{},并且它们可以任意嵌套。比如,{[] ()[{}]}或[{()}([])]等都为合法格式,而{[}()]或[({)]为不合法的格式。那我现在给你一个包含三种括号的表达式字符串,如何检查它是否合法呢?
这里也可以用栈来解决。我们用栈来保存未匹配的左括号,从左到右依次扫描字符串。当扫描到左括号时,则将其压入栈中;当扫描到右括号时,从栈顶取出一个左括号。如果能够匹配,比如“(”跟“)”匹配,“[”跟“]”匹配,“{”跟“}”匹配,则继续扫描剩下的字符串。如果扫描的过程中,遇到不能配对的右括号,或者栈中没有数据,则说明为非法格式。
当所有的括号都扫描完成之后,如果栈为空,则说明字符串为合法格式;否则,说明有未匹配的左括号,为非法格式。
七、解答开篇
好了,我想现在你已经完全理解了栈的概念。我们再回来看看开篇的思考题,如何实现浏览器的前进、后退功能?其实,用两个栈就可以非常完美地解决这个问题。
我们使用两个栈,X 和 Y,我们把首次浏览的页面依次压入栈 X,当点击后退按钮时,再依次从栈 X 中出栈,并将出栈的数据依次放入栈 Y。当我们点击前进按钮时,我们依次从栈 Y 中取出数据,放入栈 X 中。当栈 X 中没有数据时,那就说明没有页面可以继续后退浏览了。当栈 Y 中没有数据,那就说明没有页面可以点击前进按钮浏览了。
比如你顺序查看了 a,b,c 三个页面,我们就依次把 a,b,c 压入栈,这个时候,两个栈的数据就是这个样子:

当你通过浏览器的后退按钮,从页面 c 后退到页面 a 之后,我们就依次把 c 和 b 从栈 X 中弹出,并且依次放入到栈 Y。这个时候,两个栈的数据就是这个样子:
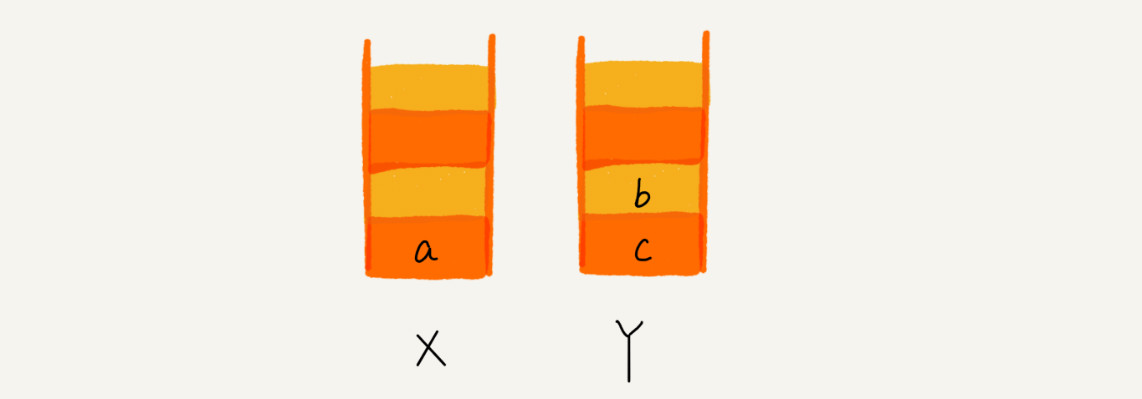
这个时候你又想看页面 b,于是你又点击前进按钮回到 b 页面,我们就把 b 再从栈 Y 中出栈,放入栈 X 中。此时两个栈的数据是这个样子:
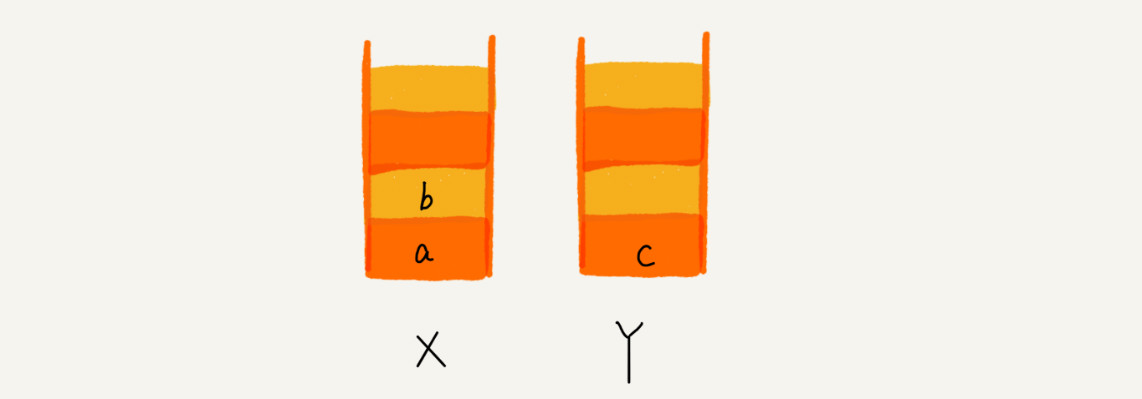
这个时候,你通过页面 b 又跳转到新的页面 d 了,页面 c 就无法再通过前进、后退按钮重复查看了,所以需要清空栈 Y。此时两个栈的数据这个样子:
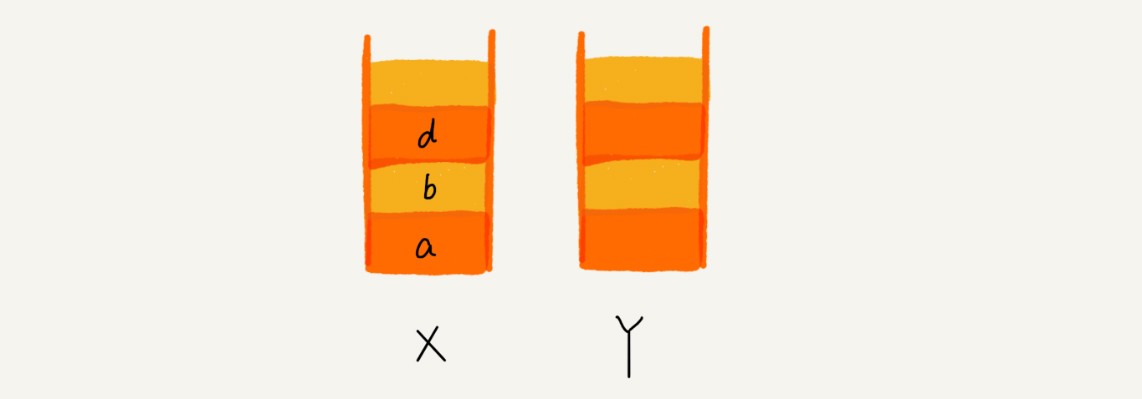
八、内容小结
我们来回顾一下今天讲的内容。栈是一种操作受限的数据结构,只支持入栈和出栈操作。后进先出是它最大的特点。栈既可以通过数组实现,也可以通过链表来实现。不管基于数组还是链表,入栈、出栈的时间复杂度都为 O(1)。除此之外,我们还讲了一种支持动态扩容的顺序栈,你需要重点掌握它的均摊时间复杂度分析方法。
思考题
- 我们在讲栈的应用时,讲到用函数调用栈来保存临时变量,为什么函数调用要用“栈”来保存临时变量呢?用其他数据结构不行吗?
- 我们都知道,JVM 内存管理中有个“堆栈”的概念。栈内存用来存储局部变量和方法调用,堆内存用来存储 Java 中的对象。那 JVM 里面的“栈”跟我们这里说的“栈”是不是一回事呢?如果不是,那它为什么又叫作“栈”呢?