学号1:211606367 姓名:林恩 学号2:211606445 姓名:肖志豪
一、预估与实际
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | 30 | 30 |
| • Estimate | • 估计这个任务需要多少时间 | 30 | 30 |
| Development | 开发 | 600 | 560 |
| • Analysis | • 需求分析 (包括学习新技术) | 70 | 50 |
| • Design Spec | • 生成设计文档 | 50 | 70 |
| • Design Review | • 设计复审 | 20 | 30 |
| • Coding Standard | • 代码规范 (为目前的开发制定合适的规范) | 30 | 20 |
| • Design | • 具体设计 | 185 | 185 |
| • Coding | • 具体编码 | 185 | 185 |
| • Code Review | • 代码复审 | 30 | 30 |
| • Test | • 测试(自我测试,修改代码,提交修改) | 30 | 30 |
| Reporting | 报告 | 60 | 50 |
| • Test Repor | • 测试报告 | 30 | 30 |
| • Size Measurement | • 计算工作量 | 10 | 10 |
| • Postmortem & Process Improvement Plan | • 事后总结, 并提出过程改进计划 | 10 | 20 |
| 合计 | 690 | 640 |
二、需求分析
我通过百度的方式了解到,小学三年级数学有如下的几个特点:
-
运算符在2~4个
-
可以加括号
-
减法运算的结果不能有负数--还需要在逆波兰计算时仍有判断
-
除法运算除数不能为0,不能有余数
-
混合运算结果不能是小数,并且括号内的数字只有两个
-
混合运算结果不超过10000
-
括号须有意义,并不能是无意义括号
-
同时,保留为一、二年级出题功能
-
除法运算不能出现小数,只能是整数
三、设计
1. 设计思路
说明你如何设计这个程序
比如类图:

- 关键函数的程序流程图是怎样的?

2. 实现方案 写出具体实现的步骤
比如:
调度场算法规则:
- 从左到右遍历中缀表达式的每个数字和符号
- 若是数字就输出,即成为后缀表达式的一部分
- 若是符号,则判断其与栈顶符号的优先级,优先级高的放在前面,是右括号或优先级低于栈顶符号(乘除优先于加减),则栈顶元素一次出栈并输出,并将当前符号进栈,一直到最终输出后缀表达式为止
将中缀表达式转换为后缀表达式(即逆波兰表达式):
- 初始化两个栈:操作数的栈s1和运算符栈s2;
- 从左至右扫描中缀表达式;
- 遇到操作数时,将其压入操作数的栈s1;
- 遇到运算符时,比较其与运算符栈s2栈顶运算符的优先级:(左右括号不弹出栈,不形成最终后缀表达式的一部分,只是对消)
- 如果s2为空,或栈顶运算符为左括号“(”,则直接将此运算符入栈;
- 否则,若优先级比栈顶运算符的高或是相同,也将运算符压入s2
- 否则,将s2栈顶的运算符弹出并压入到s1中,再次转到(4-1)与s2中新的栈顶运算符相比较;
- 栈顶符号优先级最高(除左右括号不接受排列),依照顺序优先级从高到低排列
- 遇到括号时:
- 如果是左括号“(”,则直接压入s2;
- 如果是右括号“)”,则依次弹出s2栈顶的运算符,并压入s1,直到遇到左括号为止,此时将这一对括号丢弃;
- 直到表达式的最右边;
- 将s2中剩余的运算符依次弹出并压入s1;
- 依次弹出s1中的元素并输出,结果的逆序即为中缀表达式对应的后缀表达式
逆波兰表达式求值规则:
- 从左至右扫描表达式,遇到数字时,将数字压入堆栈,遇到运算符时,弹出栈顶的两个数,用运算符对它们做相应的计算(次顶元素和栈顶元素),并将结果入栈;
- 重复上述过程直到表达式最右端,最后运算得出的值即为表达式的结果
例如后缀表达式“3 4 + 5 × 6 -”:
-
从左至右扫描,将3和4压入堆栈;
-
遇到+运算符,因此弹出4和3(4为栈顶元素,3为次顶元素,注意与前缀表达式做比较),3.计算出3+4的值,得7,再将7入栈;
-
将5入栈;
-
接下来是×运算符,因此弹出5和7,计算出7×5=35,将35入栈;
-
将6入栈;
-
最后是-运算符,计算出35-6的值,即29,由此得出最终结果。
在 Eclipse 控制台中使用 Windows 命令行
摘抄自
https://blog.csdn.net/qq_39216184/article/details/79705159
Stack.Peek 与 stack.pop 的区别:
相同点:大家都返回栈顶的值。
不同点:peek 不改变栈的值(不删除栈顶的值),pop会把栈顶的值删除。
验证一个字符串是否为double类型:
boolean isDouble(String str)
{
try
{
Double.parseDouble(str);
return true;
}
catch(NumberFormatException ex)
{
return false;
}
}
静态变量与局部变量生命周期
- 静态变量的生命周期--一直持续到整个"系统"关闭
- 当局部变量{由声明在某方法,或某代码段里(比如for循环)}一但脱离作用域,内存立即释放
四、编码
-
请说明你如何按照设计思路进行编码,并记录你在开发中遇到的问题,与解决过程
-
在使用栈stack的pop()和peek()取栈顶值时,发现了两者不同
-
因为要使用命令行来进行开发,所以后来安装了eclipse命令行工具,来进行方便操作调试
-
判断字符串是否是小数时,采用抛异常的方法,若是抛异常,即不是小数;若是没抛异常,即转成小数成功
-
了解到了前缀表达式(又称“波兰式”),中缀表达式(又称“调度场算法”),后缀表达式(“又称“逆波兰表达式”),三者算法不同,中缀表达式转成后缀表达式采用调度场算法,方便计算机快速大量计算。
-
-
结对编程
-
寻找一名队友一起编程完成任务,在编程过程中每个人都可以是驾驶员,也可以是领航员,可以互换位置,为了更快更有效率完成任务
-
结对编程是中高效的学习方法,互补不足,互相进取
-
两个通过互相探讨了解互相想法思维的不同,求同存异
-
编程上一起编写,遇到问题互相讨论
-
1. 调试日志
记录编码调试的日志,请记录下开发过程中的 debug 历程
比如:
-
在代码的什么位置,代码出现了什么问题,问题会导致什么结果,怎么解决的
-
Calculation类中计算后缀表达式值时,使用栈stack的pop()和peek()取栈顶值时,用了pop(),总是不能不删除栈顶取到值,后来了解到了peek()
-
变量名大量雷同,重复,使用时不方便,理解不便。后来采用驼峰式命名规则进行命令,根据变量,类名功能进行命名,方便理解,后期维护也容易些。
-
大量代码冗余,浪费空间,进行方法提取,有些合并了,有些缩减了。变量也开始加多设置局部变量,而不是全部都是全局变量
-
2. 关键代码
请展示一段程序的关键代码,并解释代码的作用
if(args[0].equals("-n") && args[2].equals("-grade"))
{ input_args[0] = args[1];input_args[1] = args[3];}
else if(args[0].equals("-grade") && args[2].equals("-n"))
{ input_args[0] = args[3];input_args[1] = args[1];}
else
System.out.print("输入有误!!!");
对命令行传来的数据进行判断,获取相对应的年级和题数信息,以便进行后续的计算使用。
3. 代码规范
请给出本次实验使用的代码规范:
- 第一条... 类名应为驼峰式风格且首字母大写,比如:BookShelf
- 第二条... 变量名应为下划线风格,比如:bool_shelf
- 第三条… 异常进行手动处理,不抛出。
- 第四条… 进行适当合理的代码注释,方便理解,修正
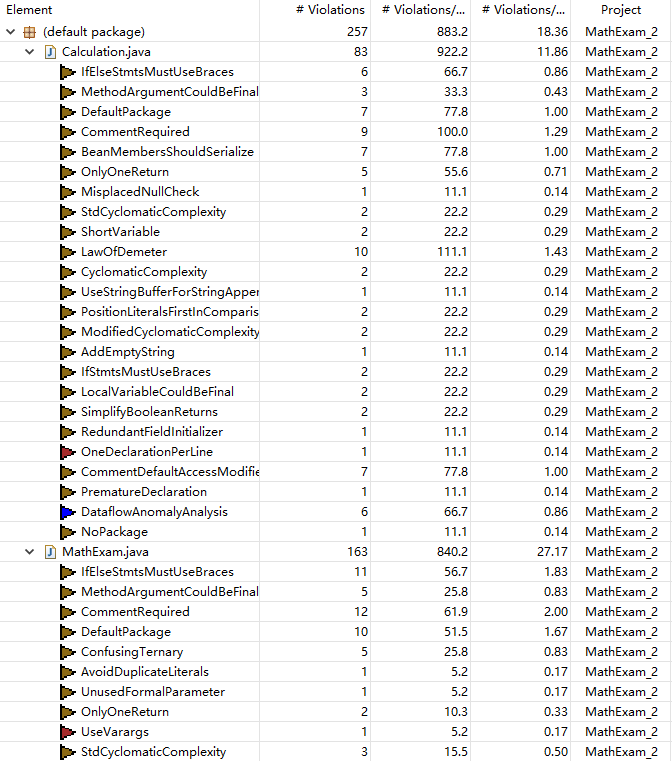
- 静态代码分析工具PMD的检查结果截图

五、测试 请思考并记录你认为必要的测试点,并记录测试用例与测试结果
| 测试用例 | 测试结果 |
|---|---|
| java MathExam -n 100 -grade 1 | 正常输出out.txt,一年级功能保留成功 |
| java MathExam -n 100 -grade 2 | 正常输出out.txt,二年级功能保留成功 |
| java MathExam -n 100 -grade 3 | 正常输出out.txt,三年级功能成功 |
| java MathExam -grade 3 -n 100 | 正常输出out.txt,三年级功能成功 |
| java MathExam -grade 32 -n 100 | 输入的年级不合法!请重新输入题数: |
| java MathExam -grade g3 -n 100 | 输入有误!!!输入的年级不合法!请重新输入年级: |
六、总结 请总结过程中的教训和经验,思考
- 非摆拍的两人的结对工作照

-
结对编程的认识和感悟
- 结对编程是中高效的编程方式,能够有效提高双方编程效率,能够互相进取,能够更加了解自己,促进交流能力
- 了解到Stack.Peek 与 stack.pop 的区别
- Eclipse插件功能强大,可生成完整类图,标准
- 不仅能用类型方法来判断变量类型。同样能通过抛异常的手段,来寻找到适合的类型
- 静态变量与局部变量生命周期,在不同函数里,局部变量和静态变量为何会不同的变化
- 了解到前缀表达式、中缀表达式(波兰表达式)、后缀表达式(逆波兰表达式)三种表达式的定义及用法,各自适用场景
- 同时,了解到在进行测试时,应该考虑的更多。白盒测试,黑盒测试都是行之有效的方法
- 为了更高效的开发实践以及后期维护,要养成良好的编程习惯及代码维护