下面给出Splay的实现方法(复杂度证明什么的知道是 nlogn 就可以啦)
首先对于一颗可爱的二叉查找树,是不能保证最坏nlogn的复杂度(可以想象把一个升序序列插入)
(二叉查找树保证左子树元素大小都小于根元素大小,根元素大小都小于右子树元素大小,且子树都是二叉查找树)
所以我们需要一些非常巧妙的旋转操作 (ratate)来优化这棵树(并让他改名叫Splay)
(图片顺序全反了2333)
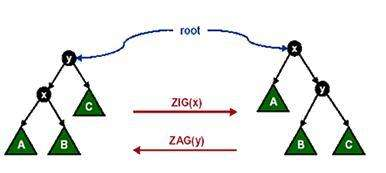
1.节点 x 的父节点 y 是根节点。这时,如果 x 是 y 的左孩子,我们进行一次 Zig (右旋)操作;如果 x 是 y 的右孩子,则我们进行一次 Zag(左旋)操作。经过旋转,x 成 为二叉查找树 S 的根节点,调整结束。
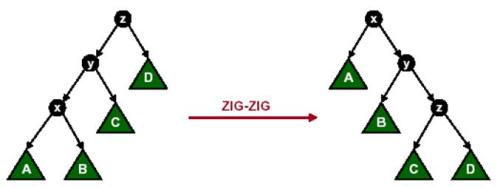
2.节点x 的父节点y 不是根节点,y 的父节点为z,且x 与y 同时是各自父节点 的左孩子或者同时是各自父节点的右孩子。这时,我们进行一次Zig-Zig操作或者Zag-Zag操作。
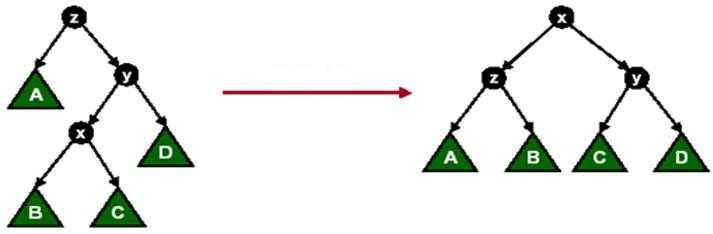
3.节点x的父节点y不是根节点,y的父节点为z,x与y中一个是其父节点的左孩子 而另一个是其父节点的右孩子。这时,我们进行一次Zig-Zag操作或者Zag-Zig 操作
在这个过程中我们完成了让x上移为的操作
假设我们已经领悟了这些操作,我们再学习一个Splay(x)函数让他不断调用Rotate,将x节点旋转到根节点,这样就完成了对SPlay的维护(实现比较简单,可以看代码)
非常重要的性质是,Rotate和Splay函数使得维护Splay树的时候无论以哪个节点为根,这棵树都是比较"优美"的(长得比较均匀)
下面着重讨论一下splay上的各种操作:
1.Find()
这个比较简单,我们只需要不断比较然后去左儿子或者右儿子即可
2.Insert()
先去Splay里面找x,如果找到了的话直接x计数器++,没找到就新建一个节点
我们只要重点考虑一下怎么维护这棵树的其他性质(例如子树大小)
回到刚刚的Splay()操作,我们可以发现,每次旋转之后旋转的节点的子树大小是可更新的,且不受到之后的影响(具体可画图理解)
所以我们可以把这个节点(新建的或者以前的)直接Splay到根节点就完成了维护
3.Getmax/min
额...直接不停往左或者往右即可
4.Earse
先考虑删除根节点(因为其他节点都是能移到根节点的)根节点的删除对子树信息没影响,所以可以直接删
然后现在剩下了两棵小树,我们只需要让一棵树接到另一棵树上即可,而这等价于让一棵树根节点的一个儿子为空
我们可以把左子树的最大儿子转到根,这样左子树的右儿子就是空的了,把右子树根节点接过去即可
5.getkth
利用计数器往左往右查找即可
6.getrank
这个别想得太复杂,直接把他转到根节点,左子树大小+1就是排名
7.getpre/nxt(找前驱后继)
转到根节点,然后直接找左子树最大值(右子树最小值)
讲到这里基本操作就OK啦,看看代码就学会了SPlay!
1 #include<cstdio> 2 #include<algorithm> 3 #include<cstring> 4 #include<cmath> 5 #define N 100010 6 #define which(x) (ls[fa[(x)]]==(x)) 7 typedef long long ll; 8 using namespace std; 9 int n,root,idx,val[N],fa[N],ls[N],rs[N],sze[N],cnt[N]; 10 int read() 11 { 12 int ret=0,neg=1; 13 char j=getchar(); 14 for (;j>'9' || j<'0';j=getchar()) 15 if (j=='-') neg=-1; 16 for (;j>='0' && j<='9';j=getchar()) 17 ret=ret*10+j-'0'; 18 return ret*neg; 19 } 20 void upt(int x)//更新子树大小 21 { 22 sze[x]=sze[ls[x]]+sze[rs[x]]+cnt[x]; 23 } 24 void rotate(int x)//旋转操作 25 { 26 //y是x父亲,z是y父亲,b是y的另一个儿子 27 int y=fa[x],z=fa[y],b=which(x)?rs[x]:ls[x],dir=which(y); 28 which(x)?(rs[x]=y,ls[y]=b):(ls[x]=y,rs[y]=b); 29 fa[y]=x,fa[b]=y,fa[x]=z; 30 if (z) dir?ls[z]=x:rs[z]=x; 31 upt(y),upt(x);//更新大小 32 } 33 void splay(int x)//把x旋转至根节点 34 { 35 //为了让树平衡,如果x和父亲同向,转fa[x]染红转x 36 //否则转两次x 37 while (fa[x]) 38 { 39 if (fa[fa[x]]) 40 if (which(x)==which(fa[x])) rotate(fa[x]); 41 else rotate(x); 42 rotate(x); 43 } 44 root=x;//现在x是根了 45 } 46 int getmin(int x)//找以x为根子树最小值节点编号 47 { 48 while (ls[x]) x=ls[x]; 49 return x; 50 } 51 int getmax(int x)//找以x为根子树最大值节点编号 52 { 53 while (rs[x]) x=rs[x]; 54 return x; 55 } 56 int find(int x)//找值为x的节点没有则返回 57 { 58 int cur=root,last=0; 59 while (cur && val[cur]!=x) 60 { 61 last=cur; 62 if (x<val[cur]) cur=ls[cur]; 63 else cur=rs[cur]; 64 } 65 return cur?cur:last; 66 } 67 void insert(int x)//插入x 68 { 69 int cur=find(x);//找到 70 //如果已经存在x,把x++后splay成根节点 71 if (cur && val[cur]==x) return (void)(cnt[cur]++,sze[cur]++,splay(cur)); 72 //如果不存在x就创造一个,然后splay 73 val[++idx]=x,fa[idx]=cur,cnt[idx]=sze[idx]=1; 74 if (cur) x<val[cur]?ls[cur]=idx:rs[cur]=idx; 75 splay(idx); 76 } 77 void erase(int x)//删除值为x的节点 78 { 79 int cur=find(x);//保证存在 80 splay(cur);//先把x转到根 81 //如果x个数大于1,直接删掉就好 82 if (cnt[cur]>1) cnt[cur]--,sze[cur]--; 83 //如果有一个儿子节点为空,直接让另一个为根,如果都是空就说明树为空 84 else if (!ls[cur] || !rs[cur]) root=ls[cur]+rs[cur],fa[root]=0; 85 else 86 { 87 fa[ls[cur]]=0;//x的左儿子没爸爸了 88 int u=getmax(ls[cur]);//让左子树最大值节点当新根节点,右子树的根节点是新根节点的右儿子 89 splay(u); 90 rs[u]=rs[cur],fa[rs[cur]]=u; 91 upt(u); 92 } 93 } 94 int getkth(int k)//寻找第k大,比较easy 95 { 96 int cur=root; 97 while (cur) 98 { 99 if (sze[ls[cur]]>=k) cur=ls[cur]; 100 else if (sze[ls[cur]]+cnt[cur]>=k) return val[cur]; 101 else k-=sze[ls[cur]]+cnt[cur],cur=rs[cur]; 102 } 103 return val[cur]; 104 } 105 int getrank(int x)//询问x排名 106 { 107 int cur=find(x); 108 splay(cur); 109 return sze[ls[cur]]+1; 110 } 111 int getpre(int x)//找前驱 112 { 113 int cur=find(x); 114 if (val[cur]<x) return val[cur]; 115 splay(cur); 116 return val[getmax(ls[cur])]; 117 } 118 int getnxt(int x)//找后继 119 { 120 int cur=find(x); 121 if (val[cur]>x) return val[cur]; 122 splay(cur); 123 return val[getmin(rs[cur])]; 124 } 125 int main() 126 { 127 n=read(); 128 for (int i=1,op,x;i<=n;i++) 129 { 130 op=read(),x=read(); 131 if (op==1) insert(x); 132 if (op==2) erase(x); 133 if (op==3) printf("%d ",getrank(x)); 134 if (op==4) printf("%d ",getkth(x)); 135 if (op==5) printf("%d ",getpre(x)); 136 if (op==6) printf("%d ",getnxt(x)); 137 } 138 return 0; 139 }