Dijkstra单源最短路径算法
Dijkstra算法是用来解决单源最短路径的经典方法。适用于带有非负数权重的单源有向图。
举例说明:
如对于以下一个图:
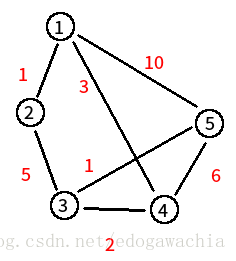
其中有5个顶点 Vertice(v),7条边 Edge (e),其中边上的数字代表边的权重 weight,假设我们以v1作为源点,想要找到从v1出发到其他各点的最短路径,其中路径长度指的是所经过的边的权重之和。那么根据dijkstra算法可以如下解决:

下面对算法的基本思路和实现过程进行解释说明:
dijkstra算法往往被认为是一种贪心法,在每一次选择节点或者说路径的时候都要找邻接的顶点中最近的一个,但是实际上找到的是全局最优路径。首先,dijkstra算法将图上的所有顶点分成两类:一类是已经找到最短路径的S;一类是还未确定最短路径的Q,显然 Q = V - S 。该算法的大致思路是,每一步都在未确定最短路径的顶点中选择距离源点最短的一个,然后认为是已经确定的最短路径,然后用它来更新剩下的点的路径长度(这个过程叫做松弛,即算法中的最后一步RELAX)。更新后继续这一步骤,直到所有的点都进入S,也就是说到所有点的最短路径都被确定下来,算法结束。
算法步骤具体如下:
- 先初始化,建立一个距离矩阵 distance ,大小为 Nv × Nv,其中Nv是顶点的数量。如果两点 i,j 之间直接相连,即邻接,那么distance( i, j ) = weight of i to j 。如两点不邻接,则distance( i, j ) = inf。置为无穷大。然后建立一个距离向量D ,长度为Nv,用来保存算法结束后计算出的从源点到每个点的最短距离。初始化D,即将源点所有邻接的点 k 的位置的D(k)的值置成源点到k的距离,不邻接为inf。D中的点现在都是未确定的,都是属于Q,此时S中只有源点自己。
- 找到D中最小的点imin,将其从Q加入S,即认为已经到该点的最短路径已经确定,就是D(imin),然后用这个点去更新未确定的点,所谓更新是指,找到imin这个点邻接的点,计算经由imin这个点到达它的邻接点的距离 D(imin) + distance(imin,thisvertice),并和D(thisvertice),即原来存储的到thisvertice的最短距离,进行比较,如果经过imin的距离即前者更小一些,那么就用这个更小的值更新D(thisvertice),这说明已经找到了另一条更近的到达thisvertice的路径。对所有的imin的邻接点做一遍,更新完毕。
- 重复2中的过程,直到所有的点都已经进入S,即都已经确定了最短路径。
- 此时D向量保存的就是源点到其他点的最短路径的值,所对应的路径在更新过程中已经得到了。
下面用上图的栗子进行解释:
首先
D = 【 0, 1, inf, 3, 10 】,最小是1(除了源点),所以V2已经确定,得到
D = 【 0, 1*, inf, 3, 10 】然后用V2去更新,发现V2连着V3,经过V2到V3为 D(2) + distance(2,3) = 6 和 D(3) = inf 相比更小,所以更新V3。得到
D = 【 0, 1*, 6, 3, 10 】然后选择V4,确定V4的最短路径就是D(4) = 3,得到
D = 【 0, 1*, 6, 3*, 10 】然后看V4与V3,V5相连,更新V3,V5得到:
D = 【 0, 1*, 5, 3*, 9 】然后选择V3,此时V3已经确定,得到:
D = 【 0, 1*, 5*, 3*, 9 】用V3更新V5,得到:
D = 【 0, 1*, 5*, 3*, 6 】选择V5,则 D = 【 0, 1, 5, 3, 6 】,至此,到所有的顶点的最短路径都已经找到。算法结束。
感觉这个算法的一个(对于小编来说)比较难理解的或者说需要进一步解释一下的点在于:为什么每次更新得到的imin就是确定的?或者换句话说,为何每次更新都能得到一个最短路径?又或者说:取出的这个点imin,存不存在一条到达它的更短的路径?
这个实际上是讲dijkstra算法的正确性问题,查了下书(CLRS),发现书中的做法如下:




基本思想就是说,如果到u(就是前面的imin)的这条路径中除了imin这个点以外还有在Q中的点y的话,那么一方面,u是Q中之min,但是又由于权重非负,所以在y后面加上一些别的点直到u,肯定路径更长,所以u既小于等于到y的路径长度,又大于等于,所以就是等于。为了利用反证法,我们y取的是第一个出S但是长度为最小路径的点。而u我们规定为第一个不满足最小路经的点,由于u是第一个不满足,因此y满足最小路径,根据前面的推理,得到u为最小路径,和规定的矛盾,因此说明加入u仍保持最小路径。
2018/01/25 21:39
为了使灵魂宁静,一个人每天要做两件他不喜欢的事。 —— 毛姆