在很多有关数据结构和算法的书籍或文章中,作者往往是介绍完了什么是树后就直入主题的谈什么是二叉树balabala的。但我今天决定不按这个套路来。我个人觉得,一个东西或者说一种技术存在总该有一定的道理,不是能解决某个问题,就是能改善解决某个问题的效率。如果能够先了解到存在的问题以及已存在的解决办法的不足,那么学习新的知识就更容易接受,也更容易理解。
万幸的是,二叉树的讲解是可以按照上述顺序来进行的。那么,今天在我们讨论二叉树之前,我们先来讨论一种情形、一种操作:假设现在有一个数组,数组中的数据按照某个关键字排好了序,现在我们希望判断某个数据是否已存在于数组中,怎么样做才更快?(为了方便起见,我们假设数组就是一个int a[n],数据就是整数)
最简单直接的办法就是从a[0]开始一直到a[n-1],将数组中的元素逐一与目标数据进行比较,那么在最坏的情况下(该数据不存在于数组中或者该数据在[n-1]),我们要比较n次才能结束查找操作。
那么,我们有没有更快速的算法来完成这个操作呢?有的,那就是二分查找。所谓二分查找,就是在有序表中,每次都让被查找数据与当前表的中间结点进行比较,根据比较结果“舍弃”掉以中间结点划分的某一半子表。
上面的说法可能比较难懂(我都觉得难懂,随手打的╮(╯_╰)╭),但我们可以举一个生活中的实例来体会一下什么是二分查找。
假设现在有一个商品的价格是1-100元之间的整数,请你猜出它的价格且猜的次数不能超过10次,请问该怎么猜?最愚蠢的办法就是用类似于顺序比较的办法,从1开始一个一个的猜,这样猜的话最坏情况下需要猜100次才能猜出来,只有10%的概率能在10次以内猜中。但是我们大家都知道一个办法,肯定能够在10次以内猜出来,那就是:先猜50,如果“大了”则继续猜25,如果“小了”则继续猜75,每一次都是猜“中间结点”,然后根据结果“舍弃掉”某一半子表,比如猜50时“大了”我们就“舍弃”了从51到100的那一半子表。通过这样的二分查找,我们可以保证在至多7次后就找到目标价格。
int binarySearch(int *a,int n,int target) { int left=0; int right=n-1; int middle=(left+right)/2; while(left!=right) { if(a[middle]==target) return middle; if(a[middle]<target) left=middle+1; if(a[middle]>target) right=middle-1; middle=(left+right)/2; } return -1; }
作为题外话,我们再来算算二分查找的时间复杂度是怎样的。
对于二分查找,我们知道两点:
1.每次我们都将表的大小减半,也就是除以二
2.最坏情况下我们要一直“除以2”直到表只剩下一个元素
综合这两点我们就会发现,二分查找花费的时间关键点就是比较了多少次,而比较的次数在最坏情况下就是表的大小n不断除以2直至n为1的次数。这样以来我们很快就能得出二分查找的时间复杂度:O(log2N)(也可以忽略底数2记为O(logN))
好了,对于二分查找的介绍就到此为止。接下来我们探讨一个新的问题:如果我们希望表的大小能够动态的变化该怎么办?不假思索的回答是使用双向链表(因为有时候我们需要向前寻找 ,所以双向是有必要的)。但其实链表(不论是否是双向)根本不适合使用二分查找。为什么呢?因为在数组中,我们比较中间结点与被查找数据时可以直接使用下标来找到中间结点,如a[50],但是在链表中,我们如果要比较第50个结点与被查找数据,我们不得不“经过”前49个结点,也就是说,虽然比较操作依然是一次,但是类似于middle=middle->next这样的操作将会随着“中间结点”所在的位置而变化,在最坏情况下(假设要查找的数据在表尾),我们将不得不“走遍”整个链表,也就是类似middle=middle->next的操作我们不得不执行n次,最终算法的时间复杂度依然是O(n)。
那么,是否存在一种数据结构可以既支持二分查找,又支持动态变化大小呢?幸运的是,有的,那就是二叉树。
在学习普通的树时,我们对每个结点有多少个孩子没有做出限制,而二叉树则是对每个结点能有几个孩子做出了限制的树。在二叉树中,一个结点最多有两个孩子,这也是“二叉”的取名原因。(下图为一棵二叉树)

由于每个结点的最大孩子数是固定的,所以我们可以将结点定义改为如下:
typedef struct BinaryTreeNode { int data; int frequency; //当插入数据与当前结点相同时+1,当删除当前结点时-1 struct BinaryTreeNode *left; //指向左孩子 struct BinaryTreeNode *right; //指向右孩子 }BinaryTreeNode; typedef BinaryTreeNode *BinaryTree;
二叉树显然是支持动态变化大小的(当然,它的删除操作与我们之间模拟的文件系统树是不一样的,我们简单地令frequency--来表示删除该结点,若结点的frequency<=0,则表示该结点“不存在”),我们要明白的就是为什么它能够支持二分查找。之前说过,链表“不支持”二分查找的原因就是我们访问某个中间结点时不得不“走一遍”其前面(或后面)的结点,那么二叉树是如何避免这个过程的呢?很简单,让我们一步一步看看。
稍微分析二分查找的话,我们不难发现,二分查找的基本要求是数据有序。如果我们要让二叉树支持二分查找,就必须让二叉树中的数据也实现“有序”。那么二叉树中该如何实现数据“有序”呢?很简单,那就是让每个结点都满足左子树中的所有结点均小于本结点,右子树中的所有结点均大于本结点。经过这样的“改造”的二叉树,就是我们所说的二叉查找树。对于上述数据量为100的情况,我们暂且假设有这样一棵二叉查找树
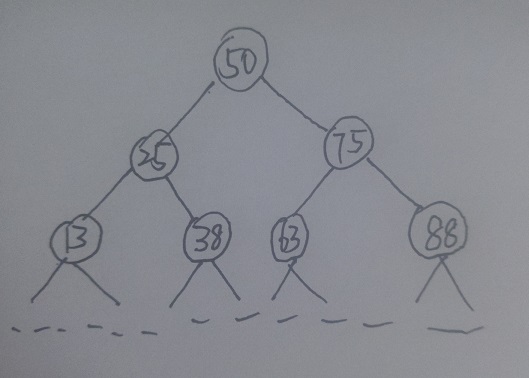
稍微看看这棵树就会发现二分查找可以“完美地”应用于其中,当我们拿着给定数据进入树时,首先访问到的就是原表中的中间结点,如果给定数据大于该结点,则我们向该结点的右子树寻找(此时我们又将恰好地访问到子表的中间结点),反之向该结点的左子树寻找,且对于每一个结点我们都保持这种做法,最终我们可以找到目标数据,或者因为到达某结点,其不存在孩子且该结点亦非目标数据,则目标数据不存在。
因此,二分查找应用于二叉查找树时的代码如下:
bool searchByTree(BinaryTree t,int data) { if (t == NULL) return false; if (t->data == data&&t->frequency > 0) return true; if (data < t->data) return searchByTree(t->left, data); if (data > t->data) return searchByTree(t->right, data); return false; }
而要想满足二叉查找树的性质,插入结点的代码就应该如下:
BinaryTree Insert(BinaryTree t,int data) { if (t == NULL) { BinaryTree temp = (BinaryTree)malloc(sizeof(BinaryTreeNode)); temp->data = data; temp->frequency = 1; temp->left = temp->right = NULL; return temp; } if (data < t->data) t->left = Insert(t->left, data); else if (data > t->data) t->right = Insert(t->right, data); else t->frequency++; return t; }
现在我们有了实现插入的办法了,该如何实现上面假设的那棵完美的二叉查找树呢?很不幸的是,如果你要这样完美的(完美匹配二分查找)二叉查找树,那你只能先将数据在数组中排好序,然后将其按二分查找的访问顺序将数组元素逐个插入到二叉树中,而且你之后也不能再插入新结点,因为那样必将打破其完美的特性。可是如果这样做的话,我们又为什么还需要二叉查找树呢?所以实际使用的时候,我们往往是直接将随机数据插入到二叉树,这样做的话最后生成的二叉查找树有可能是长这样的(左右严重不平衡)

这样的二叉查找树已经不能完美匹配二分查找了,但是!二叉查找树依然很好的同时实现了快速查找和动态变化大小。所以二叉查找树依然是一种很有意义的数据结构(其实二叉树还有其他的应用,比如赫夫曼编码,有兴趣的可以去查来看看)。
接下来,我们看看如何实现二叉查找树中的删除操作。
之前我们定义结点的时候为结点保留了一个frequency域,当我们要插入的新数据已存在于树中时,我们将对应结点的frequency加一以表示该数据在树中的实际个数。所以在删除结点时我们也可以利用这个frequency,即删除结点时递减frequency即可。即使frequency递减至0,我们也依然保留该结点。这样的删除实现我们称之为“懒惰删除”,其好处在于实现简单、快速,坏处则是结点需要额外的空间。
//懒惰删除 void lazyDelete(BinaryTree t, int data) { if (t == NULL) return; if (t->data == data && t->frequency > 0) t->frequency--; if (data < t->data) return deleteNode(t->left, data); else return deleteNode(t->right, data); }
如果希望实际地删除结点,就会更麻烦一点。首先我们要明白,被删除结点可能有三种状态:无孩子,有一个孩子,有两个孩子。
对于无孩子的情况,我们直接释放被删除结点即可。
对于只有一个孩子的情况,我们令其孩子替代其位置,然后释放被删除结点即可。(下图假设删除结点4)
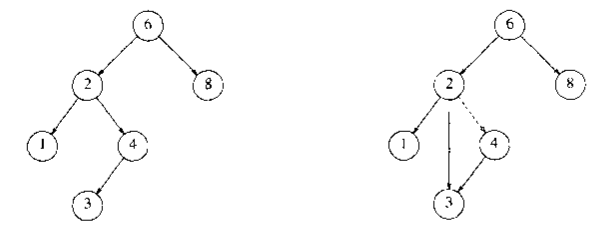
对于有两个孩子的情况,处理则稍微麻烦一点,因为我们还要保持二叉查找树的基本特征。所以我们可选的操作有两种:
将被删除结点的数据修改为左子树中最大结点的数据,然后删除左子树中最大的结点;
将被删除结点的数据修改为右子树中最小结点的数据,然后删除右子树中最小的结点。
假设我们选择用右子树的最小结点替代,下图为删除结点2的示意
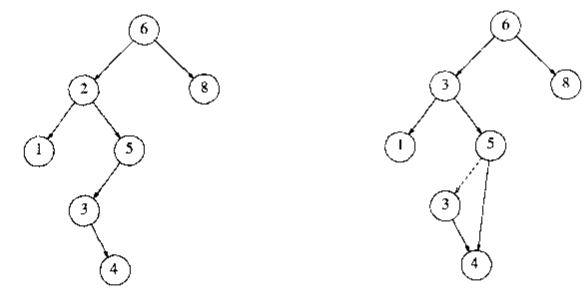
知道了上述三种情况该如何应对后,我们就可以写出删除结点的代码了:
BinaryTree deleteNode(BinaryTree t, int data) { if (t == NULL) return t; //若被查找数据小于当前结点 if (data < t->data) t->left = deleteNode(t->left, data); //若被查找数据大于当前结点 else if (data > t->data) t->right = deleteNode(t->right, data); //如果t即需要删除的结点,且有两个孩子 else if (t->left&&t->right) { t->data=getMinData(t->right); t->right=deleteNode(t->right,t->data); } //否则t只有一个孩子或没有孩子,我们均可以用以下代码处理 else { BinaryTree temp = NULL; temp = (t->left) ? t->left : t->right; free(t); return temp; } return t; }
上面的代码中我们没有写出getMinNode()的实现,这个函数的实现并不困难,但我们还是要提一提它,为什么呢?因为我们在getMinNode()的时候,我们其实已经“走到了”右子树的最小结点处,但是我们没有将其删除,而是在后面调用deleteNode(t->right,t->data)时才去将其删除!也就是说我们在这条路径上走了两趟!所以改进的措施就是写一个特殊的deleteMin()函数,令其返回子树最小结点数据的同时删除该结点。
BinaryTree deleteMin(BinaryTree t,int *minData) {
if(t==NULL)
return t; //若当前结点t没有左孩子,则t必为最小的结点 if (t->left == NULL) { *minData = t->data; BinaryTree temp = t->right; free(t); return temp; } //若当前结点有左孩子,则删除其左子树中的最小结点 else t->left = deleteMin(t->left, minData); return t; }
然后将deleteNode()中当t有两个孩子时的代码修改为如下:
else if (t->left&&t->right) { int minData; t->right = deleteMin(t->right,&minData); t->data = minData; }
这样一来,我们就在这条路径上只走了一遍。
在删除结点时被删除结点有两个孩子的解决办法中,我们使用了一点儿小技巧(右子树的最小结点)来保证了二叉查找树的性质不被改变。那么,我们能通过某种技巧令整棵二叉树在不断的Insert和deleteNode时尽量保持左右子树的平衡(即深度尽可能相似)吗?答案是能!下一篇博文我们就将介绍什么是平衡二叉树。其可以很好的应用于经常查找,偶尔插入、删除的情境下!
最后,给出一个简单对比无序数组查找和二叉查找树查找效率的程序,在给定数据量为1000时两者的效率就可以有较大差别(根本原因是程序中查找时每到一个非目标结点均暂停1毫秒,如果不这么做,在我的电脑上需要数据量达到1000万才能比较出两者的效率差异)
https://github.com/nchuXieWei/ForBlog------binarySearchTree
———————————————————————————补充————————————————————————————————
在树的学习中,我们提到了对树的两种遍历方法:先序遍历和后序遍历。但是在二叉树中,我们还有一种遍历的方法叫做“中序遍历”,因为每个结点的孩子数最多就是两个,所以我们可以选择先处理左子树,再处理结点本身,再处理右子树。而这样的遍历就叫中序遍历(如果不懂的话可以去看我写的(10))。那么中序遍历有什么特殊之处呢?
假设我们对一棵二叉查找树进行中序遍历,遍历时的操作就是将当前结点输出到某个数组的尾巴(遍历开始前该数组为空),那么一趟中序遍历下来,那个数组中的元素是不是已经排好了序呢?显然是的!那么通过二叉树来实现对数据的排序是否可行呢?这个我们以后将会讨论。
temp =