最小比率树 poj2728

  以下内容均为转载

http://www.cnblogs.com/ftae/p/6947497.html

poj2728（最小比率生成树）

 

poj2728

题意

给出 n 个点的坐标和它的高度，求一颗生成树使得树上所连边的两点高度差之和除以距离之和最小。

分析

01分数规划+最小生成树。
对于所有的边，在求最小生成树过程中有选或不选的问题，
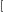
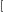
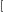
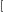
首先根据01分数规划，我们要使 l=∑i=1nheight[i]∗exist[i]∑i=1ndis[i]∗exist[i] (exist[i]表示是否有这条边)最小，
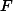
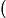
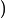
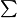
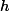
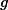
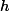
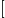
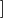
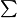
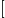
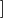
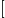
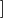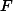
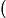
设 F(l)=∑height[i]∗exist[i]−l∗∑dis[i]∗exist[i] ，我们要使 l 尽可能的小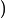， F(l) 随 l 减小而递增，如果 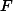F(l)<0 ，
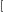
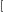
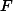
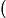
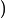
∑i=1nheight[i]∗exist[i]∑i=1ndis[i]∗exist[i]<l ，即存在更优的 l ，当 F(l)=0 时，即为最终最终答案 l 。
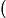
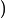
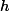
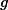
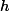
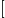
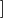
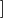
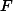
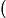
设 D(l)=height[i]−dis[i]∗l ，把它作为边，求最小生成树，那么求得值 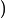F(l) 一定是尽可能小的，越有可能出现更优的 l 。

本题适于采用迭代法，因为在求最小生成树的过程中，就可以计算出更优的 l 值。

code（二分法）

#include<cstdio>
#include<cstring>
#include<cmath>
#include<iostream>
#include<algorithm>
using namespace std;
typedef long long ll;
const int MAXN = 1e3 + 10;
const double INF = 1e15;
int n;
double dist(double x1, double y1, double x2, double y2) {
    return sqrt((x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2));
}
struct node {
    double x, y, h;
}a[MAXN];
double height[MAXN][MAXN];
double map[MAXN][MAXN];
double dis[MAXN];
int vis[MAXN];
double prime(double rate) {
    double sum = 0;
    memset(vis, 0, sizeof vis);
    for(int i = 1; i <= n; i++) {
        dis[i] = INF;
    }
    dis[1] = 0;
    for(int i = 0; i < n; i++) {
        double MIN = INF;
        int k;
        for(int j = 1; j <= n; j++) {
            if(!vis[j] && dis[j] < MIN) MIN = dis[k = j];
        }
        vis[k] = 1;
        sum += MIN;
        for(int j = 1; j <= n; j++) {
            if(!vis[j] && dis[j] > height[k][j] - rate * map[k][j]) {
                dis[j] = height[k][j] - rate * map[k][j];
            }
        }
    }
    return sum;
}
void solve() {
    double l = 0, r = 1e5, mid = 0;
    while(r - l > 1e-6) {
        mid = (l + r) / 2;
        if(prime(mid) < 0) r = mid;
        else l = mid;
    }
    printf("%.3f
", mid);
}
int main() {
    while(cin >> n && n) {
        for(int i = 1; i <= n; i++) {
            cin >> a[i].x >> a[i].y >> a[i].h;
            for(int j = 1; j <= i; j++) {
                map[i][j] = map[j][i] = dist(a[i].x, a[i].y, a[j].x, a[j].y);
                height[i][j] = height[j][i] = abs(a[i].h - a[j].h);
            }
        }
        solve();
    }
    return 0;
}

code（迭代法）

#include<cstdio>
#include<cstring>
#include<cmath>
#include<iostream>
#include<algorithm>
using namespace std;
typedef long long ll;
const int MAXN = 1e3 + 10;
const double INF = 1e15;
int n;
double dist(double x1, double y1, double x2, double y2) {
    return sqrt((x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2));
}
struct node {
    double x, y, h;
}a[MAXN];
double height[MAXN][MAXN];
double map[MAXN][MAXN];
double dis[MAXN];
int vis[MAXN], pre[MAXN];
double prime(double rate) {
    double sum = 0;
    double sumh = 0, sumd = 0;
    memset(vis, 0, sizeof vis);
    for(int i = 1; i <= n; i++) {
        dis[i] = INF;
        pre[i] = 0;
    }
    dis[1] = 0;
    for(int i = 0; i < n; i++) {
        double MIN = INF;
        int k;
        for(int j = 1; j <= n; j++) {
            if(!vis[j] && dis[j] < MIN) {
                MIN = dis[k = j];
            }
        }
        vis[k] = 1;
        sum += MIN;
        sumd += map[pre[k]][k];
        sumh += height[pre[k]][k];
        for(int j = 1; j <= n; j++) {
            if(!vis[j] && dis[j] > height[k][j] - rate * map[k][j]) {
                dis[j] = height[k][j] - rate * map[k][j];
                pre[j] = k;
            }
        }
    }
    return sumh / sumd;
}
void solve() {
    double k = 0, tmp;
    while(1) {
        tmp = prime(k);
        if(fabs(tmp - k) < 1e-6) break;
        else k = tmp;
    }
    printf("%.3f
", k);
}

int main() {
    while(cin >> n && n) {
        for(int i = 1; i <= n; i++) {
            cin >> a[i].x >> a[i].y >> a[i].h;
            for(int j = 1; j <= i; j++) {
                map[i][j] = map[j][i] = dist(a[i].x, a[i].y, a[j].x, a[j].y);
                height[i][j] = height[j][i] = abs(a[i].h - a[j].h);
            }
        }
        solve();
    }
    return 0;
}