Page Rank
Time Limit: 3000/1500 MS (Java/Others) Memory Limit: 100000/100000 K (Java/Others)Total Submission(s): 280 Accepted Submission(s): 75
Problem Description
Evaluation and rank of web pages is a hot topic for many internet companies and researchers. PageRank is a link analysis tool and it assigns a numerical weighting to each element of a hyperlinked set of documents, such as the World Wide Web, with the purpose
of "measuring" its relative importance within the set. The algorithm may be applied to any collection of entities with reciprocal quotations and references. The numerical weight that it assigns to any given element E is referred to as the PageRank of E and
denoted by . Other factors like Author Rank can contribute to the importance of an entity.
For simplicity, in this problem PageRank vector q is defined as q = Gq, Where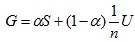 , S is the destination-by-source stochastic matrix, U is all one matrix, n is the number of
nodes and α is the weight between 0 and 1 (here we use 0.85).
, S is the destination-by-source stochastic matrix, U is all one matrix, n is the number of
nodes and α is the weight between 0 and 1 (here we use 0.85).
For the example on the right, we have:

Denote the current PageRank vector and the next PageRank vector by qcur and qnext respectively. The process is to compute the iterative powering for finding the first eigenvector.
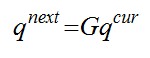
The computation ends until for some small ε(10-10).
for some small ε(10-10).
For simplicity, in this problem PageRank vector q is defined as q = Gq, Where
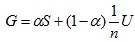 , S is the destination-by-source stochastic matrix, U is all one matrix, n is the number of
nodes and α is the weight between 0 and 1 (here we use 0.85).
, S is the destination-by-source stochastic matrix, U is all one matrix, n is the number of
nodes and α is the weight between 0 and 1 (here we use 0.85).For the example on the right, we have:

Denote the current PageRank vector and the next PageRank vector by qcur and qnext respectively. The process is to compute the iterative powering for finding the first eigenvector.
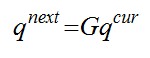
The computation ends until
 for some small ε(10-10).
for some small ε(10-10).
Input
The input contains many test cases.
For each case, there are multiple lines. The first line contains an integer N(N<=3000), which represents the number of pages. Then a N*N zero-one matrix follows. The element Eij (0 <= i, j < N) on the matrix represents whether the i-th page has a hyper link to the j-th page.
For each case, there are multiple lines. The first line contains an integer N(N<=3000), which represents the number of pages. Then a N*N zero-one matrix follows. The element Eij (0 <= i, j < N) on the matrix represents whether the i-th page has a hyper link to the j-th page.
Output
Output one line with the eigenvector. The numbers should be separated by a space and be correctly rounded to two decimal places.
Sample Input
4 0111 0011 0001 0100
Sample Output
0.15 1.49 0.83 1.53
Source
Recommend
模拟,,,
add函数没有卵用。。
ac代码
Problem : 5097 ( Page Rank ) Judge Status : Accepted
RunId : 14492913 Language : C++ Author : lwj1994
Code Render Status : Rendered By HDOJ C++ Code Render Version 0.01 Beta
#include<stdio.h>
#include<string.h>
#include<math.h>
#define eps 1e-10
char map[3030];
double ans[3030][3030];
double q[2][3030];
int n;
void muti(double a[][3030],double num)
{
int i,j;
for(i=0;i<n;i++)
{
for(j=0;j<n;j++)
a[i][j]*=num;
}
}
void add(double a[][3030],double b[][3030])
{
int i,j;
for(i=0;i<n;i++)
{
for(j=0;j<n;j++)
a[i][j]+=b[i][j];
}
}
int jud()
{
double ans=0;
int i;
for(i=0;i<n;i++)
{
ans+=(q[0][i]-q[1][i])*(q[0][i]-q[1][i]);
}
//ans=sqrt(ans);
if(fabs(ans)<eps)
return 1;
return 0;
}
int main()
{
//int n;
while(scanf("%d",&n)!=EOF)
{
int i,j;
double a=0.85;
memset(ans,0,sizeof(ans));
for(i=0;i<n;i++)
{
int sum=0;
scanf("%s",&map);
for(j=0;j<n;j++)
{
if(map[j]=='1')
sum++;
//U[i][j]=1;
}
for(j=0;j<n;j++)
{
if(map[j]=='1')
ans[j][i]=1.0/sum;
}
}
muti(ans,a);
// muti(U,1.0/n*(0.15));
// printf("
");
// add(ans,U);
for(i=0;i<n;i++)
for(j=0;j<n;j++)
ans[i][j]+=(0.15/n);
int p=0;
for(i=0;i<n;i++)
{
q[p][i]=1;
q[p^1][i]=0;
}
//mmuti(q[p],ans,q[p^1]);
//p^=1;
while(!jud())
{
//q[p^1]=mmuti(q[p],ans);
for(i=0;i<n;i++)
{
q[p^1][i]=0;
for(j=0;j<n;j++)
q[p^1][i]+=q[p][j]*ans[i][j];
}
p^=1;
}
printf("%.2lf",q[p][0]);
for(i=1;i<n;i++)
{
printf(" %.2lf",q[p][i]);
}
printf("
");
}
}