其实这名字有点拗口。
简单来说就是:
一个已知的数组(知道其所有属性),
然后在选出数组中的一个元素,
再让程序求出这个元素在数组的索引。
其实有两种做法:
第一种就是最简单的,先把这个数组遍历一遍,一个一个去比较,看看哪个相等。
第二种就是我们要讲的一个算法:二分法查找
首先来看到的第一种方法
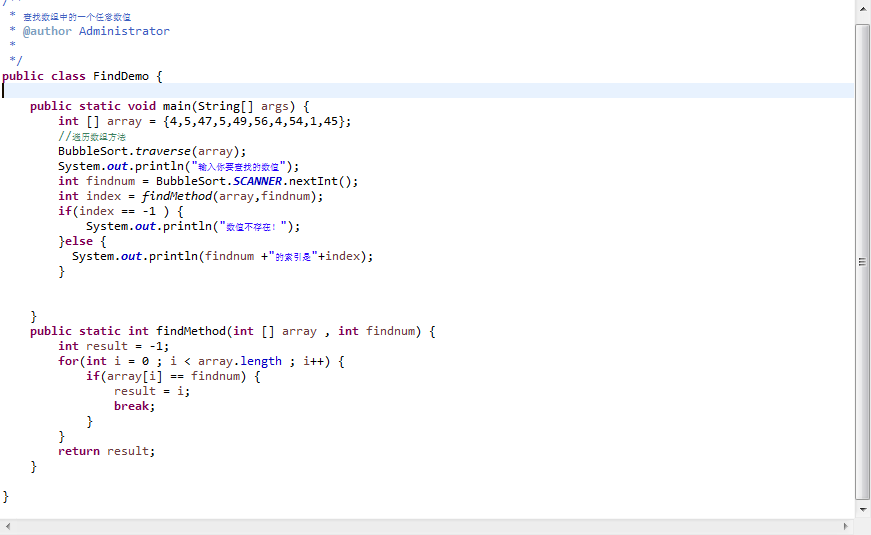
其实这个思路就很简单,就是上面说的。
先遍历,在去一个一个比较。假如比较到了就赋值索引,然后跳出循环。
这个方法有个缺点就是费时,虽然说程序运行中看不出,可是我们知道这是最没有效率的方法。
然后我们在看到第二种方法:
二分法,只不过这种方法有个缺点,就是数组必须要是顺序排列的。
这个算法的大概思路是这样的:
如一个数组:

假如我们要求出这里6的索引,用二分法如何做呢?
在开始之前我们要知道三个变量:
最小索引:不就是0吗
最大索引:不就是数组长度减去1吗
以及中间索引:不就是最大索引加上最小索引除以2的值吗
好了,有了这三个值接下来就开始比较了。
首先,使用中间索引的值去与findnum也就是要找的数比较。
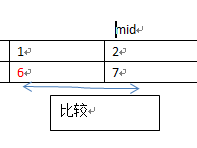
然后发现中间索引的值大于findnum的值,这时要做一件事就是去更新上面的三个值
既然findnum小于中间索引的值,那么中间索引后面的值都可以去掉。
min = 还是等于0
max = 等于当前的中间索引
mid = 还是和上面的公式一样
这时的三个索引变成了这样

然后在去拿中间索引的值和findnum比较。
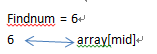
然后发现这个值就是我们要找的,然后返回这个中间索引就行了。
其实不止这一种情况,还有大于的情况。
和小于的差不多只不过是min和max这两个东西的更新不一样而已
接下来就给出代码:
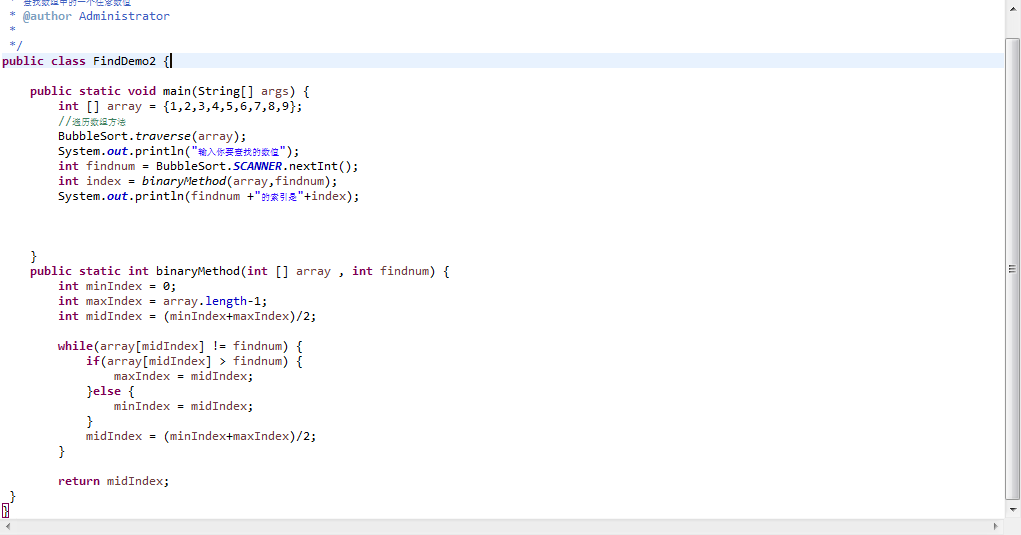
这里方法最主要的就是如何去更新这三个索引
让我们看到这个方法:
这三个索引一开始都被定义出来,赋值了
然后while循环,假如中间索引的值不等于findnum就一直循环
不等于就只有两种情况:大于和小于
假如大于的话说明这个数就不在mid和max索引之间
然后就吧mid到max这段去掉,更新max=mid
小于的话情况刚好相反
去掉min到mid这段,更新min = mid
然后每次循环更新一个mid
如果循环条件为false时会跳出循环,
这时表示mid索引的值就会等于findnnum
然后返回这个mid索引就行了
现在有一个问题就是假如数组是降序排列的
那么该怎么做呢?
其实很简单,只需要把if中的大于换成小于
二分法最最重要的一点就是数组要有序排列。