设实数$lambda >0$,若对任意的$xin(e^2,+infty)$,不等式$lambda e^{lambda x}-ln x>0$恒成立,则$lambda$的最小值为_____

提示:反函数,由题意$e^{lambda x}ge dfrac{ln x}{lambda}$,注意到$y=e^{lambda x}$与$y=dfrac{ln x}{lambda}$ 是互为反函数.
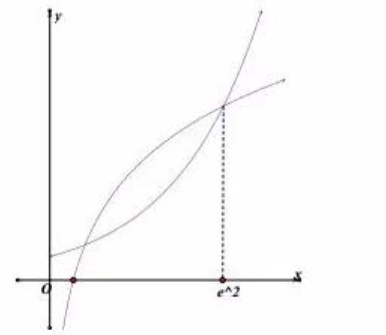
求$y=x$与$y=e^{lambda x}$的切点易得为$(e,e)$此时$lambda=dfrac{1}{e}$.由于$xin (e^2,+infty)$结合图像知$lambdagedfrac{2}{e^2}$
注:若条件改为$x>0$时恒成立,则$lambdage dfrac{1}{e}$.此时$e^{lambda x}ge e^{dfrac{1}{e}x}ge x$.
(这一步用到了常见不等式$e^x=e*e^{x-1}ge ex$)
由反函数图像知道此时$e^{lambda x}ge xgedfrac{ln x}{lambda}$成立.
练习:已知函数$f(x)=me^x-lndfrac{x}{m}(m>0)$,若关于$x$的不等式$f(x)>0$恒成立,求$m$的取值范围_____
答案$left(dfrac{1}{e},+infty
ight)$