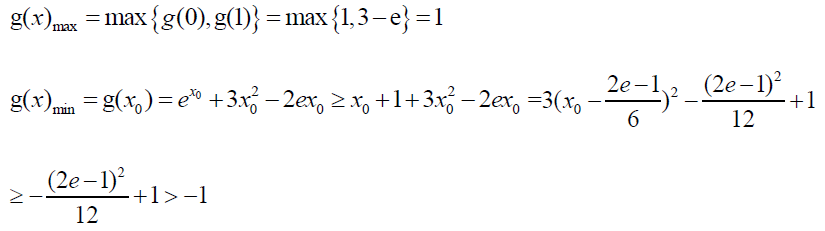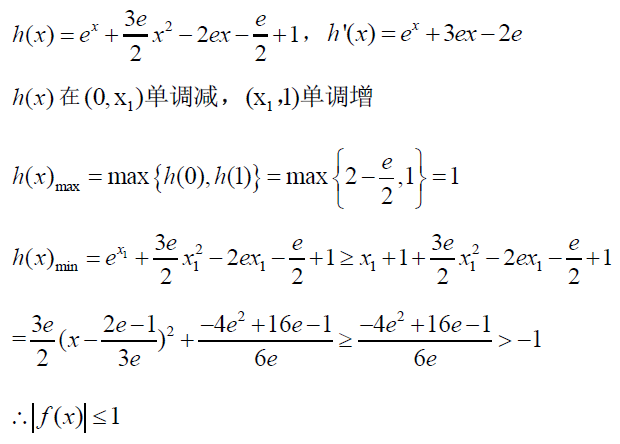已知$a>0$,函数$f(x)=e^x+3ax^2-2e x-a+1$,
(1)若$f(x)$在$[0,1]$上单调递减,求$a$的取值范围.
(2)$|f(x)|le1$对任意$xin[0,1]$恒成立,求$a$的取值范围.

解答:(1)略(2)的几何意义:
首先$|f(0)|le1,|f(1)|le1$得$1le ale dfrac{e}{2}$
又$f^{''}(x)=e^x+6a>0$,故$f(x)$图像是下凸的.且$int_0^1f(x)dx=[e^x+ax^3-ex^2+(1-a)x] {|^1}_0=0$
即$y=f(x)$图像在$x$ 轴下方的面积和上方的面积一样.
记$f^{'}(x_0)=e^x_0+6ax_0-2e=0$显然$x_0in[0,1]$.如图,
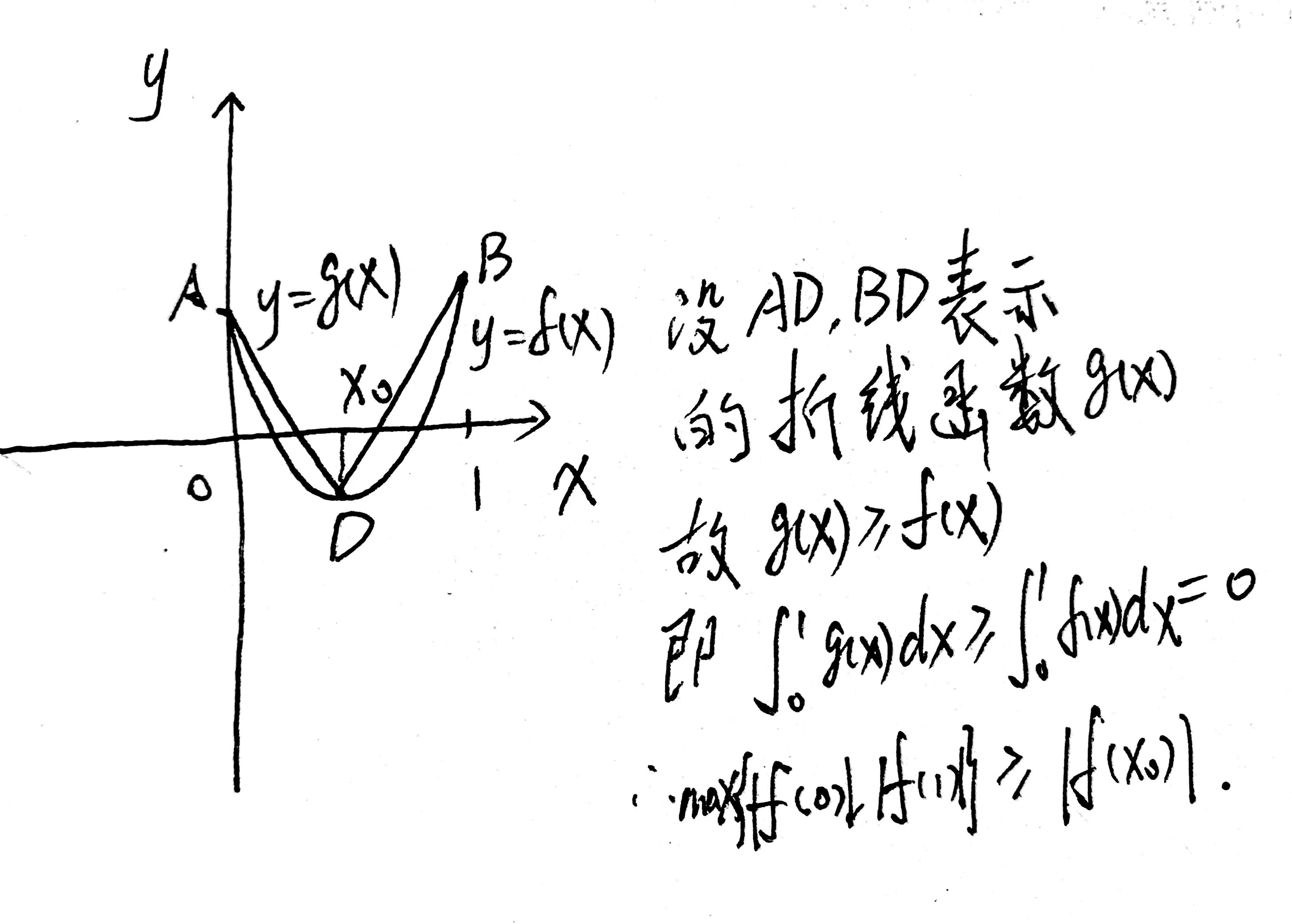
易知$|f(x)|_{max}=max{|f(0)|,|f(1)|}$
所以$1le ale dfrac{e}{2}$
附参考答案: