说人话搞懂【极大似然估计】和【最大后验概率】的区别
什么是先验/后验概率
我们先给出一些符号定义，令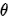
表示模型参数，
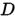表示数据。
先验概率比较好理解，比如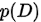 
就表示数据的先验概率（prior probability）。
但是在之前我经常搞不明白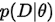 
和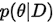
哪个才是后验概率（posterior probability）。其实二者都可以看做是后验概率，只不过少了定语。具体来说 
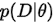是数据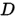 
的后验概率，即已经告诉你模型参数 
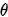了，要你求数据的概率，所以是后验概率。同理
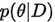是告诉你数据后，让你求
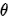的后验概率。所以，要根据语境去判断哪个才是后验概率。
似然概率
下面介绍一下贝叶斯公式这个老朋友了，或者说是熟悉的陌生人。
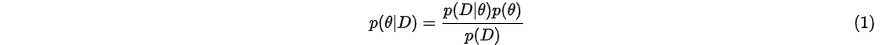
假设我们研究的对象是变量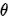
，那么此时先验概率就是 
，（
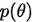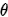的) 后验概率是
。
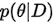那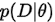
是什么呢？它就是本文的另一个主角：似然概率 （likelihood probability）,顾名思义是给定参数
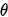，求数据是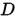
的概率是多少。
一般来说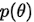 
是不知道的或者说很难求解，但是我们可以知道后验概率和 （似然概率乘以先验概率）呈正相关关系，所以
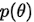即使不知道也不影响对后验概率的求解。
极大似然估计 与 最大后验概率估计
极大似然估计 （Maximum Likelihood Estimate, MLE）和最大后验概率估计（Maximum A Posteriori (MAP) estimation）其实是两个不同学派的方法论。
MLE是频率学派模型参数估计的常用方法，它的目的是想最大化已经发生的事情的概率。我们在用神经网络训练分类器的时候其实就可以理解成是MLE。具体来说，假设数据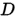
由一组数据样本组成，即
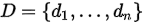，模型参数用
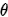表示，我们假设每个样本预测彼此独立，所以MLE的求解方式如下：
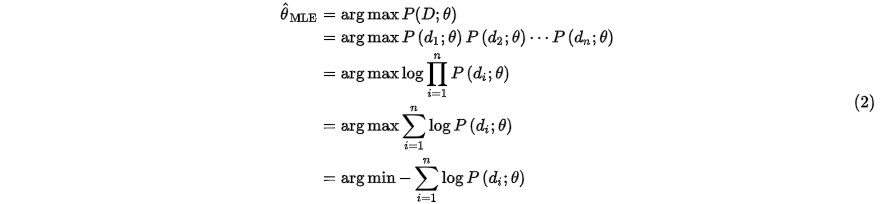
可以看到，上面其实就是我们常用的交叉熵损失函数。那么如何用MAP来优化模型参数呢？公式如下：
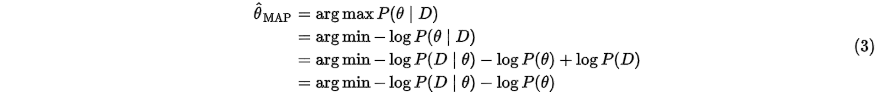
可以看到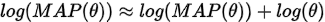 
。而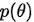
其实就是常用的正则项，即对模型参数的约束。